固定翼多种PID学习总结

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

固定翼多种PID学习总结
参考如下：
参考一
参考二

PID介绍

位置PID

e(k): 用户设定的值（目标值） - 控制对象的当前的状态值

比例P : e(k)

积分I : ∑e(i) 误差的累加

微分D : e(k) - e(k-1) 本次误差-上次误差

顾名思义，位置PID是通过不同时间下位置的变化量作为误差，通过P,I,D三个比例系数进行控制。

此处重点讲下积分项I：
【1】在位置PID算法中，因为有积分项I的存在，一旦积分饱和，也就是积分累计的误差太大，当你想反向输出时，积分项却让你的系统一直正向输出(因为积分项之前一直在累计正向误差)，这就是积分饱和，解决方法是积分分离，后面会讲到。
【2】因此在位置PID中多用PD控制。
【3】适用于舵机快速响应，平衡小车的直立和温控系统的控制。
对于惯性较大的对象，常常希望能加快控制速度， 此时可增加微分作用。
特点：
比例控制对于惯性较大对象，控制过程缓慢，控制品质不佳。比例微分控制可提高控制速度，对惯性较大对象，可改善控制质量，减小偏差，缩短控制时间。
理想微分作用持续时间太短， 执行器来不及响应。实际使用中，一般加以惯性延迟，称为实际微分。
PD 调节以比例调节为主，微分调节为辅，PD调节是有差调节（被调量与设定值之间将产生不可避免的偏差）。
PD 调节具有提高系统稳定性、抑制过渡过程最大动态偏差的作用。
PD 调节有利于提高系统响应速度。
PD 调节抗干扰能力差，一般只能应用于被调参数 变化平稳的生产过程。
微分作用太强时，容易造成系统振荡。

增量PID

比例P : e(k)-e(k-1) 本次误差-上次误差
积分I : e(i) 误差
微分D : e(k) - 2e(k-1)+e(k-2) 这次误差-2*上次误差+上上次误差
增量式PID根据公式可以很好地看出， 一旦确定了 KP、TI 、TD，只要使用前后三次测量值的偏差， 即可由公式求出控制增量
而得出的控制量▲u(k)对应的是近几次位置误差的增量，而不是对应与实际位置的偏差 没有误差累加

【1】算式中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果；
【2】计算机每次只输出控制增量，即对应执行机构位置的变化量（这里不理解的可以自己设一个期望值和三个渐变的实际值举例子看一下），故机器发生故障时影响范围小、不会严重影响生产过程；
【3】 手动—自动切换时冲击小。当控制从手动向自动切换时，可以作到无扰动切换。

位置和增量PID的关系

【1】位置式的PD控制相当于增量式PID的PI控制
位置式的D为偏差e(t)，而增量式的I也为偏差e(t)
【2】位置式需引入初始阀位值，增量式不需要
【3】位置式需防积分饱和，增量式不会产生积分饱和（因为增量式没有累加关系，这个地方可能会与位置式的积分混淆。）
【4】只有存在偏差时，增量式才会有输出
【5】增量式容易实现从手动到自动的切换
【6】位置式PID控制的输出与整个过去的状态有关，用到了误差的累加值;而增量式PID的输出只与当前拍和前两拍的误差有关，因此位置式PID控制的累积误差相对更大;
【7】增量式存在稳态误差

串级PID

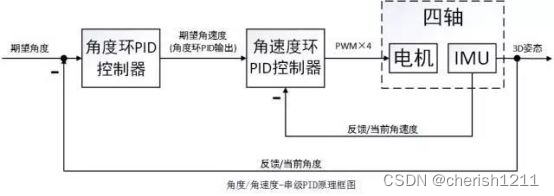
【这是在网上能找到可以很好表达串级PID的一张图片】
以固定翼控制为例：

角度环：*******************加速环
期望值 实际值 *************期望值 *********实际值
打舵量 欧拉角 *************角度环输出值 陀螺仪输出

使用串级PID的原因：
【个人理解】比如只用位置pid控制舵机，那么输出值就是所要转动的角度值。感觉很合理，就是你让舵机转多少度嘛，但是仔细分析下舵机转动这个过程，物体做运动（舵机转动），现有加速度，再有速度，再有角度，所以当角度为零的时候，角速度和角加速度不一定为零，这样就可能产生误差。

模糊PID

自适应模糊PID

优化PID方法