无损压缩编码（上）：LZ编码——详解LZ77 (LZSS)、LZ78和LZW的编码与译码

LZ77和LZ78由Abraham Lempel和Jacob Ziv分别于1977年和1978年发表，LZ即为Lempel和Ziv的首字母拼在一起。1984年Terry Welch在LZ78的基础上进行改进，发表了LZW（即Lempel–Ziv–Welch）编码。三种编码均为无损压缩编码，旨在不产生信息失真的同时降低信息冗余度。

三种编码的核心在于，按顺序读取待编码数据流，如果后面的数据流出现了前面出现过的内容，就用某种方式把这些相同的部分用某种记号来替代掉，如果记号占用的空间比原数据流更小，就能实现无损压缩。例如，如果有一字符串ABCABC，只需要记成2ABC即可，这样就可以在不失真的情况下记录更少的字符，降低信息冗余度。这种用记号替代的方式，不需要事先检索一遍整个数据流，而是相当于拿着本字典一边读取数据流一边翻译，因此也被称为字典编码；而霍夫曼编码、算术编码等则是基于概率统计的编码。

LZ77 (LZSS)

编码

对于LZ77编码而言，它使用一个滑窗（sliding window）来读取待编码数据流，比如一个字符串。滑窗由两部分组成——一部分用于缓存特定大小的待编码的数据，称为待编码缓存（lookahead buffer）；一部分用于缓存特定大小的已编码的数据，称为搜索窗（search window)，当我们用代码实现LZ77编码时首先需要指定这两个区域的大小，整个滑窗的大小通常记为W。

(有些人以为sliding window指的就是search window，这实际上是错误的）

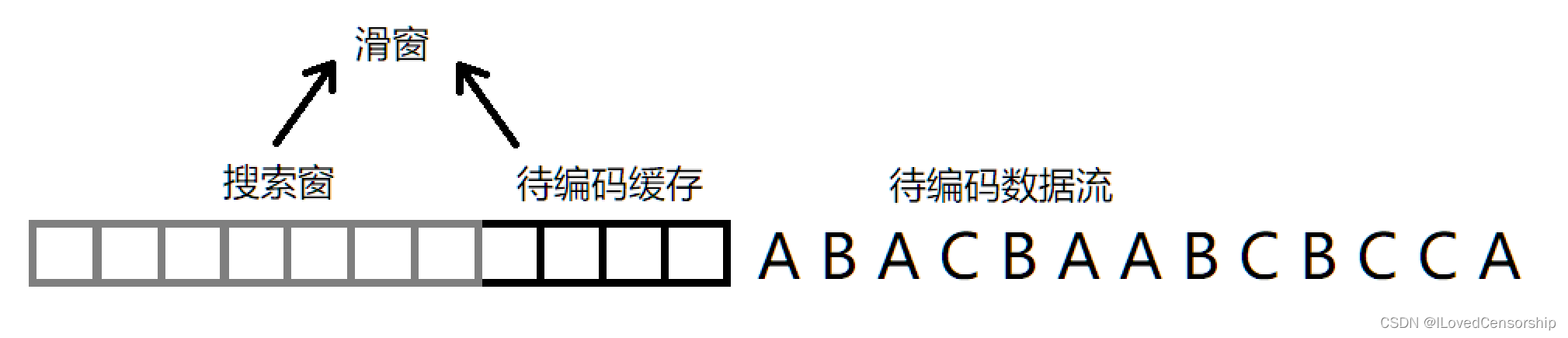
原始码为ABACBAABCBCCA

窗口向右滑动，依次读取数据，下图是编码的起始状态

LZ77编码的输出为长度-距离对（length-distance pairs），记为(D,L)c；D代表偏移量或距离，L代表匹配字符串长度，c代表字符串（char），接下来我将详细解释这三个值是怎么来的。

每完成一次编码，滑窗都向右移动距离L（除了一种情况，下面会解释），从待编码缓存左侧输出的值进入到搜索窗，有时候也把搜索窗称为字典，因为搜索窗的内容起到字典的作用；为了方便，以下简称待编码缓存为LAB（lookahead buffer）。

要产生编码输出，就要在搜索窗内找到与lab内容匹配的字符串。首先从lab中的左起第一个字符开始找，本例中为A；如果搜索窗中有匹配的字符串，则从左起前两个字符串开始找，本例中为AB，依此类推...直到在搜索窗中能找到整个lab内容（本例中为ABAC）为止。一旦搜索窗中找不到更长的匹配字符串了，则输出"DLC"，而现在我们的搜索窗为空，当然找不到任何匹配字符串了。在这种初始状态下，D=0，L=0，c=lab中的第一个字符，本例中为A；即输出为(0,0)A。

完成一次输出后，窗口向右滑动，如下图所示

L实际上是搜索窗与lab的最长匹配字符串的长度，如果没有匹配字符串，L=0，但窗口仍然向右滑动，滑动的距离为1；这就是当没有匹配字符串时，滑动距离的特殊情况。滑动窗口是为了让已经编码过的部分数据进入搜索窗内，而给lab填充还没编码的数据，即”腾出lab的空间“。

现在搜索窗中已经有了一个字符A，但显然在lab中，B、BA、BAC、BACB都与A不匹配；不匹配时的输出和初始状态一样，都是(0,0)c=lab中的第一个字符，这里的输出为(0,0)B。不匹配时，窗口右滑一格，如下图：

现在，搜索窗内的字符串为AB，lab中组合为A、AC、ACB、ACBA，显然lab中的A是可以与搜索窗中左起第一个A匹配的；搜索窗中这个与之匹配的A，距离lab两格；或者说，搜索窗中这个与之匹配的A，是从lab中向左偏移2格得到的；因此D指的是搜索窗中最长匹配字符串左起第一个字符与lab的距离，所以管D叫距离或者偏移量。这里D=2，而最长匹配字符串为A，最长匹配字符串长度L=1，输出为(2,1)，窗口右滑L=1格。注意，如果有匹配字符串，则不需要输出c；实际上，有些地方把c称为explicit bytes。现在，你已经掌握了LZ77的编码了，让我们继续：

输出(0,0)C，窗口右滑一格

此时，搜索窗中的BA与lab中的BA匹配，L=2；D是搜索窗中BA的B到lab的距离，D=3，输出(3,2)，窗口右滑2格

输出(6,2)，右滑2格

输出(5,2)，右滑2格

现在新的问题出现了，lab中的C在搜索窗中有两个位置可以匹配，我们取搜索窗最左边的匹配字符串，因此输出(7,1)，右滑1格。在有多个等长的最长匹配字符串时，选最左边的匹配字符串，即取更大的D值，是因为在实际代码中，靠左侧的匹配字符串是遍历过程中后找到的，此时直接输出效率更高。

输出(3,1)，右滑1格

输出(7,1)，右滑1格

lab中已经空了，编码结束

最终的输出为(0,0)A(0,0)B(2,1)(0,0)C(3,2)(6,2)(5,2)(7,1)(3,1)(7,1)

怎么样，是不是很简单？显然，对同一个字符串而言，选取的搜索窗和待编码缓存的大小不同，编码结果也不同

这里有一个小规律，D和L只要有一个为0，另一个必为0。因此，对于没有匹配字符串的情况，实际存储时还可以更简化，用0A就可以代替(0,0)A。但相信大家马上就发现一个问题了，比如本例的第一个编码(0,0)A，即使简化了，使用LZ77还是需要两个字符0A来表示，而这两个字符表示的实际上就是一个字符A，编码反而让需要存储的内容变得更多了！这还不如不编码。而如果(D,L)pairs表示的匹配字符串为单个字符，也就是L=1，也存在同样的问题；比如本例中最后一个字符A使用编码(7,1)表示反而更复杂。因此在更真实的应用场景中，对于L<3的情况应当不编码。

参考[MS-WUSP]: LZ77 Compression Algorithm | Microsoft Learn

实际上，LZSS正好改进了LZ77的这一缺陷：当编码比原始码占用更多空间时则不编码，直接输出原始码字；当然，由于原始码字有可能和编码输出的格式相同，因此还需要加上用于区分的标记。

总结一下，LZ77的原始编码过程如下

       1.初始化，用待编码数据流填充LAB

　　2.在LAB中查找搜索窗中的最长匹配字符串

　　3.如果找到最长匹配字符串，输出(D, L)， 窗口向右滑动L格

　　4.如果没有找到任何匹配字符串，输出(0,0)c，窗口向右滑动1格

　　5.如果LAB不为空，返回2

伪代码如下

while input is not empty domatch := longest repeated occurrence of input that begins in windowif match exists thend := distance to start of matchl := length of matchc := char following match in inputelsed := 0l := 0c := first char of inputend ifoutput (d, l, c)discard l + 1 chars from front of windows := pop l + 1 chars from front of inputappend s to back of window
repeat

解码

还是以上面的结果为例，编码结果为(0,0)A(0,0)B(2,1)(0,0)C(3,2)(6,2)(5,2)(7,1)(3,1)(7,1)

(0,0)A和(0,0)B这种D和L是0的，直接输出c即可

每输出一次字符，搜索窗就加上刚才的输出字符；搜索窗起始为空，最大长度需要提前知道

(0,0)A输出A，字典（搜索窗）由空变为A

(0,0)B输出B，字典由A变为AB

到了(2,1)，记住D是到待编码缓存（LAB）最左侧，即到字典最右侧的距离，L是最长匹配字符串的长度；此时字典为AB，D=2的位置为A，长度是1，则输出为A，字典变为ABA

(0,0)C输出C，字典由ABA变为ABAC

到了(3,2)，字典中右起第三位是B，L=2，则还要再往左找一位（因为编码时即如此），输出BA，字典由ABAC变为ABACBA

(6,2)，输出为AB，字典本应为ABACBAAB；但字典一共只有7位，所以应当去掉最左边的一位，变成BACBAAB

(5,2)，输出为CB，字典由BACBAAB变为CBAABCB

(7,1)，输出为C，字典由CBAABCB变为BAABCBC

(3,1)，输出为C，字典由BAABCBC变为AABCBCC

(7,1)，输出为A

把输出连起来，最终的解码输出为ABACBAABCBCCA，这和我们编码前的结果完全一致

为了更直观的表达，有时也会通过列表的方式进行编码和解码，例如对

 A    A    B    C    B    B    A    B    C

进行编码和解码，可以列成如下两个表

编码：

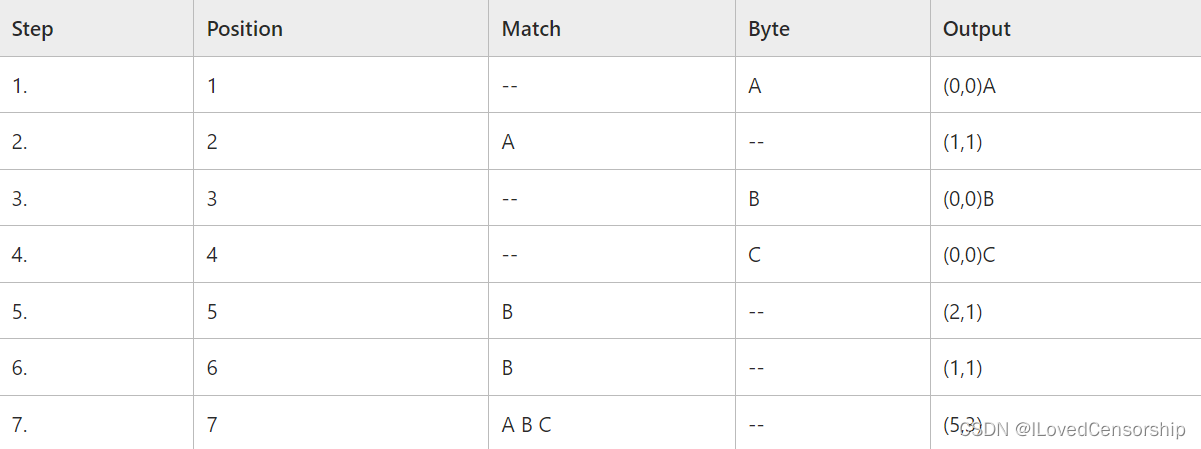
解码：

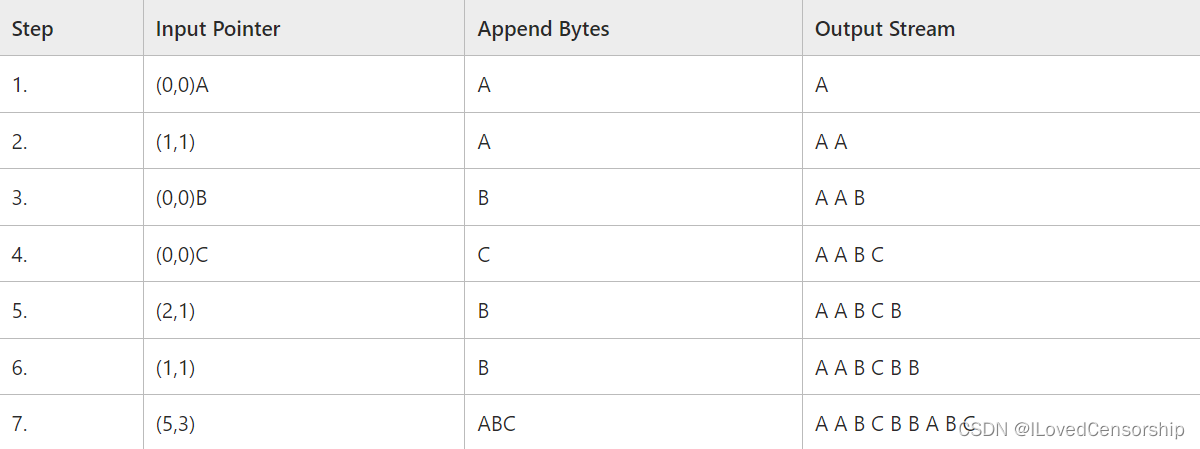
这实际上是Microsoft Learn里面的一个例子，Position是原始码中每个字符的位置；Match代表最长匹配字符串；Byte即为explicit byte（显露字节），实际上就是无匹配字符串时lookahead buffter中的左起第一个字符，我们之前将它记为c。编码的输出与最长匹配字符串的位置有关，因此也把输出编码称为输出指针。

本章节参考资料：

LZ77 and LZ78 - Wikipedia

Lempel–Ziv–Storer–Szymanski - Wikipedia

[MS-WUSP]: LZ77 Compression Algorithm | Microsoft Learn

LZ77压缩算法编码原理详解(结合图片和简单代码) - 转瞬之夏 - 博客园 (cnblogs.com)

详解LZ77字典编码压缩和解压缩流程（典型的压缩算法）_lz77压缩算法_雷恩Layne的博客-CSDN博客

LZ78

和LZ77以及LZW相比，LZ78的名声没那么大；但考虑到LZW是基于LZ78改进而来，因此了解LZ78仍是有意义的。 

编码

LZ77的字典是定长的搜索窗，每次进行查找匹配时只对定长区域进行匹配，如果已经完成的编码超出了搜索窗的范围，超出的部分就没有用了。而LZ78则是在编码过程中生成一个字典，压缩结束后这个字典不需要被保存在压缩文件中，而且随着编码的进行，其效率会越来越高（直到字典满了为止）；按照规范解码时，字典也会同步生成。LZ78的编码输出为(prefix,char)，即缀-符串（string）接下来我将详细解释这两个值是怎么来的。

还是以我们前面用过的字符串ABACBAABCBCCA为例

首先读入A，此时字典为空；因此把A放入字典中，索引（index）为1；在初始状态下，prefix=0，char=读入的第一个字符，也就是A，输出(0,A)

然后读入B，此时字典为A=1；和LZ77一样，在LZ78中我们也需要对读入的字符和字典进行匹配，匹配方式和LZ77也类似，有时也被称为最长匹配：

【

        假如读入字符是ABBA，字典中已有A，AB，ABB；那么按照我们之前LZ77的匹配规则，

        显然应该把字典中的ABB和读入字符进行匹配。

        也就是说，输入的待编码字符，和字典进行匹配时，我们要找的是最长的匹配字符串。

        当字典不能与输入字符完全匹配时，如字典中有XY，而输入字符为XYZW，

        最长匹配字符串被称为prefix（前缀），如这里的XY；

        至于剩下的部分，我们取出其左起第一个字符，作为char，如这里的Z；

        但我们肯定不能直接把XY作为前缀，否则就没有编码的意义了，

        而是把XY对应的索引作为前缀输出，例如XY对应的Index是20，则输出(20,Z)；

        同时，把前缀+char作为一个整体存入字典，并赋予新的索引。

        当字典完全不能与输入字符匹配时，输出prefix=0，char=读入的当前字符；

        并把当前读入的字符存入字典，赋予新的索引

        当字典能完全与输入字符匹配时，则继续输入字符，直到不能匹配为止；

        除非完全匹配的字符是原始数据流的最后一个字符，否则完全匹配时都不输出编码。

】

现在回到读入B这里，字典中的A=1和B不匹配，把B存入字典，索引为2，我们将其记作B=2，输出(0,B)

读入A，A在字典中能找到A=1，继续读入下一个字符C；AC在字典中找不到，只能匹配到A；此时A为前缀，prefix=A的索引=1，char=C，输出(1,C)，把AC=3存入字典

读入B，B在字典中有B=2，继续读入A得到BA，前缀为B，prefix=2，char=A，输出(2,A)，把BA=4存入字典

读入A，能匹配；读入B得AB，前缀为A，prefix=1，char=B，输出(1,B)，AB=5存入字典

读入C，无匹配，输出(0,C)，把C=6存入字典

读入B，能匹配，读入C得BC，前缀为B，prefix=2，char=C，输出(2,C)，BC=7存入字典

读入C，能匹配，读入A得CA，前缀为C，prefix=6，char=A，输出(6,A)，CA=8存入字典

因此，ABACBAABCBCCA在LZ78编码下的输出为(0,A)(0,B)(1,C)(2,A)(1,B)(0,C)(2,C)(6,A)

LZ78下的编码有8组，占用空间比LZ77下更小（不信自己翻回去数），但仍然出现了不少单字符被编码成2个字符导致占用空间变大的情况，这导致LZ78对小文件的效率不高（LZW也一样）

这里还有一个问题，如果在上述原始码的后面加上一个字典中已知的单字符，比如C；这个时候，编码器读入C，直接可以和字典匹配，但后面已经没有多的数据可供继续读入了；此时直接输出该单字符的索引，即(prefix,)；在这里输出的就是C的索引6。

继续考虑上述情况，末尾加上一个C之后整个原始码的输出可以记为0A0B1C2A1B0C2C6A6；在实践中，由于C后面没有东西了，因此给它加上一个文件终止记号（EOF marker）”＄“，此时的输出为0A0B1C2A1B0C2C6A6＄

现在，你已经完全掌握LZ78的编码了！接下来让我们一起学习它的译码

译码

我们用刚才修改过的原始码，即ABACBAABCBCCAC＄对应的编码输出0A0B1C2A1B0C2C6A6＄来译码

写成更好认的形式(0,A)(0,B)(1,C)(2,A)(1,B)(0,C)(2,C)(6,A)6

(0,A)和(0,B)这种prefix为0的可以直接译成单字符：(0,A) = A = 1，(0,B) = B = 2

每译出一个包含char的编码，意味着这个译码结果在目前的字典中是没有的，因此要将该译码结果录入字典并赋予索引

接下来是(1,C)，记住1代表的是索引为1的字符，这里当然是A，因此(1,C) = AC = 3

然后是(2,A) = BA = 4，(1,B) = AB = 5，(0,C) = C = 6，(2,C) = BC = 7，(6,A) = CA = 8；

最后剩一个6 = C，因此译码结果为ABACBAABCBCCAC，和前面的结果完全一致，并且编码字典和译码字典也一定是完全一样的。

提到字典，还有最后一点需要注意：显然我们的字典是不能无限大的，字典的大小必须一开始就指定好。那如果在编码过程中，字典容量已经满了，但字典中仍需生成新内容时又该如何处理呢？

有两种比较好理解的方案：一是停止生成字典，使用旧字典继续编码，缺点是后面有字典匹配不到的内容就无法编码了，只能跳过；二是清除旧字典并从头开始构建新的字典，这相当于把整个文件分成了几块，每块都有一个独立的字典。

本章节参考资料：

LZ77 and LZ78 - Wikipedia

【数据压缩】LZ78算法原理及实现_lz压缩算法_Lucky0928的博客-CSDN博客

数据压缩与LZ系列算法及其改进_weixin_30588907的博客-CSDN博客

LZW

LZW算法相当有名，GIF和TIFF格式就使用了LZW，实际上这也是笔者唯一一个在教科书上学过的LZ编码。和LZ78不同，LZW需要先初始化一个字典，把一些单字符先存入字典，即初始字典；然后再用类似LZ78的方式进行编码：逐个读入字符并与字典进行最长匹配，如果能完全匹配则不输出，而是继续读入字符；如果部分匹配，则输出前缀对应的码字，并把此时的字符串存入字典，剩余不能匹配的部分保留在缓存中，等待读入下一个字符。在实际应用中不会出现完全不能匹配的情况，因为初始字典应当覆盖256个ASCII字符（包括正负），所以至少一个字符串的第一个字符一定是匹配的。不过在我们做演示的时候，通常不会给出这么完整的字典，只会给出A=1，B=2，C=3这种简易的初始字典，因此用于演示的数据流也只会是ABC三个字符的组合。

现在以ABBABCAABCB为例演示LZW的编码和译码，并讨论它相对于LZ78的优势。

编码

首先指定初始字典A=1，B=2，C=3

开始读入字符A，字典中能匹配到A=1，继续读入下一个字符

继续读入B，得AB，在字典中只能匹配到A=1，因此把AB=4存入字典，输出A对应的索引1，剩余字符串为B

继续读入B，得BB，在字典中只能匹配到B=2，因此把BB=5存入字典，输出B对应的索引2，剩余字符串为B

继续读入A，得BA，在字典中只能匹配到B=2，因此把BA=6存入字典，输出B对应的索引2，剩余字符串为A

继续读入B，得AB，在字典中能匹配到AB=4，因此继续读入C，最长匹配字符串为AB，因此把ABC=7存入字典，输出AB对应的索引4，剩余字符串为C

继续读入A，得CA，在字典中只能匹配到C=3，因此把CA=8存入字典，输出C对应的索引3，剩余字符串为A

继续读入A，得AA，在字典中只能匹配到A=1，因此把AA=9存入字典，输出A对应的索引1，剩余字符串为A

继续读入B，得AB，在字典中能匹配到AB=4，因此继续读入C，在字典中能匹配到ABC=7，因此继续读入B，最长匹配字符串为ABC，因此把ABCB=10存入字典，输出ABC对应的索引7，剩余字符串为B

B在字典中有，而后面已经没有新的字符需要输入了，直接输出B对应的索引2

编码结束，输出为12243172

和LZ78相比，LZW相当于只需要输出prefix而不需要输出char，因此在一些场景下占用空间更小；但实际应用中的LZW需要先存储一个初始大字典（虽然只有8Byte），而LZ78不用。

译码

还是用上面的例子，已知初始字典A=1，B=2，C=3，对编码输出12243172进行译码

译码过程中，生成新字典的方式和编码一样：

        编码时，在当前字符串能匹配的情况下，读入下一个字符，与当前字典进行匹配，如果匹配不上，则把当前字符串+下一个字符作为整体录入字典中。

        译码时，在当前密码能被翻译的情况下，把上一个译码结果和当前译码结果的第一个字符作为整体录入字典中。

1在初始字典中就有，译为A

2也在初始字典，译为B；而AB在字典中没有，把AB=4写入字典

2在初始字典中有，译为B；而BB在字典中没有，把BB=5写入字典

4在字典中有，译为AB；而BA在字典中没有，把BA=6写入字典

3在字典中有，译为C；而ABC在字典中没有，把ABC=7写入字典

1在字典中有，译为A；而CA在字典中没有，把CA=8写入字典

7在字典中有，译为ABC，而AA在字典中没有，把AA=9写入字典

2在字典中有，译为B，后面已经没有新字符了，译码结束

最终的译码结果为ABBABCAABCB，和原始的字符串一致，字典也一致

但是在LZW译码的过程中还会出现一种特殊情况，如果编码输出的最后一个码字是字典中的最后一个索引，那么在译码时，因为字典输出比译码要慢，所以会出现无法确定最后一个译码结果（即字典中最后一个单词）的情况。以字符串ABABCBABCCC为例，初始字典依然是A=1，B=2，C=3

读入字符        当前字符串        最大匹配字符串        输出编码        字典更新        剩余字符        

A                        A                        A                                

B                        AB                     A                                1                  AB=4                B

A                        BA                     B                                2                  BA=5                A

B                        AB                     AB

C                        ABC                  AB                              4                  ABC=6             C

B                        CB                    C                                3                  CB=7                B

A                        BA                     BA                                                                           

B                        BAB                  BA                              5                  BAB=8              B

C                        BC                    B                                2                  BC=9                C

C                        CC                    C                                3                  CC=10              C        

C                        CC                    CC                             10

编码输出为1,2,4,3,5,2,3,10

此时，最后一个编码输出恰好是字典中的最后一项，如果我们正常译码：

读入码字        当前译码输出        字典更新

1                        A

2                        B                        AB=4

4                        AB                      BA=5

3                        C                        ABC=6

5                        BA                      CB=7

2                        B                        BAB=8

3                        C                        BC=9

10                      ??     

这时你会发现，字典中还没有索引10；只有当10对应的原码被翻译出来，才能进行字典更新，把??=10添加到字典中，这似乎是一个悖论。但实际上，按照字典构造的规则，10对应的原码一定是C?的形式；因为译码构造字典是把上一个译码输出和当前译码输出的第一个字符作为字典中的新一项 ，而这里上一个译码输出为C，所以，C?=10，且?只能代表单个字符。因此把上表中10对应的译码输出替换成C?，再考虑一遍字典构造规则，既然已经知道当前译码输出的第一个字符是C了，那么字典中新生成的项自然应该是【上一个译码输出的C】加上【当前译码输出的第一个字符】，也就是CC。最终译码结果为ABABCBABCCC，准确无误。

通过这个案例我们可以得知，如果LZW编码的过程中，最后一个编码结果是字典中最后生成的索引；那么在译码时，最后一项的结果一定是在倒数第二项译码输出的末尾加上其第一个字符（如果倒数第二项译码输出是XYZ，那么最后一项译码输出是XYZX）

LZW和LZ78都面临着字典会随着压缩的进行而变满的问题；对于LZW而言，如果字典满了就清空字典（原始字典不清空），那么压缩效率会在字典清空后迅速降低。一种更合理的解决方案是，发现压缩效率降低到某个阈值时才清空字典，这样能减少清空字典的次数，从而在一定程度上提高压缩效率。

本章节参考资料：

Lempel–Ziv–Welch - Wikipedia

Python实现LZW编码与译码_lzw编码 python_我是无殇呀的博客-CSDN博客

《信息论基础教材》第3版（李梅、李亦农等）