True Liars（带权并查集+dp）

题目链接：https://vjudge.net/problem/POJ-1417

题目大意：世界上有两种人，一种是好人，他们说的每句话都是实话；另一种人是坏人，他们说的每句话都是假话。你可以问他们别人（包括他自己）是不是好人，他们会给你"yes"或者"no"的回答。现在给出n次提问，并且告诉你了好人和坏人人数，问你是不是有且只有一种合法的情况。如果是，就顺序输出好人；如果不是就输出"no" 

​​​​​​​思路参考：True Liars （POJ - 1417）带权并查集+dp路径_AC__dream的博客-CSDN博客

思路：

        我们对于他们的回答来分析一下，假设你问A：B是不是好人：如果Ａ的回答是"yes"，那么又可以分为两种情况：1.Ａ是好人：那么Ｂ也是好人；2.A是坏人，那么B也是坏人。如果A的回答是“no”，同样存在两种情况：1.A是好人，那么B就是坏人；2.A是坏人，那么B就是好人。

        我们可以发现：如果回答的是"yes"，那么不论是不是好人，首先A和B必是同一种人；如果回答是“no”，那么A和B必是不同种的人

        那么这就非常类似与带权并查集的处理方式，我们用节点与根节点的距离来代表两者之间的关系，我们假设：如果与根节点的距离是0，那么这个节点和根节点是一种人；如果与根节点的距离是1，那么这个节点和根节点就不是一种人

        那么就会涉及到路径压缩的问题，当我每次merge的时候应该如何更新旧爸爸到新爸爸之间的距离并且不改变代表的含义呢，如下图所示，要将x和ymerge起来，我们要新处理的边是dis:

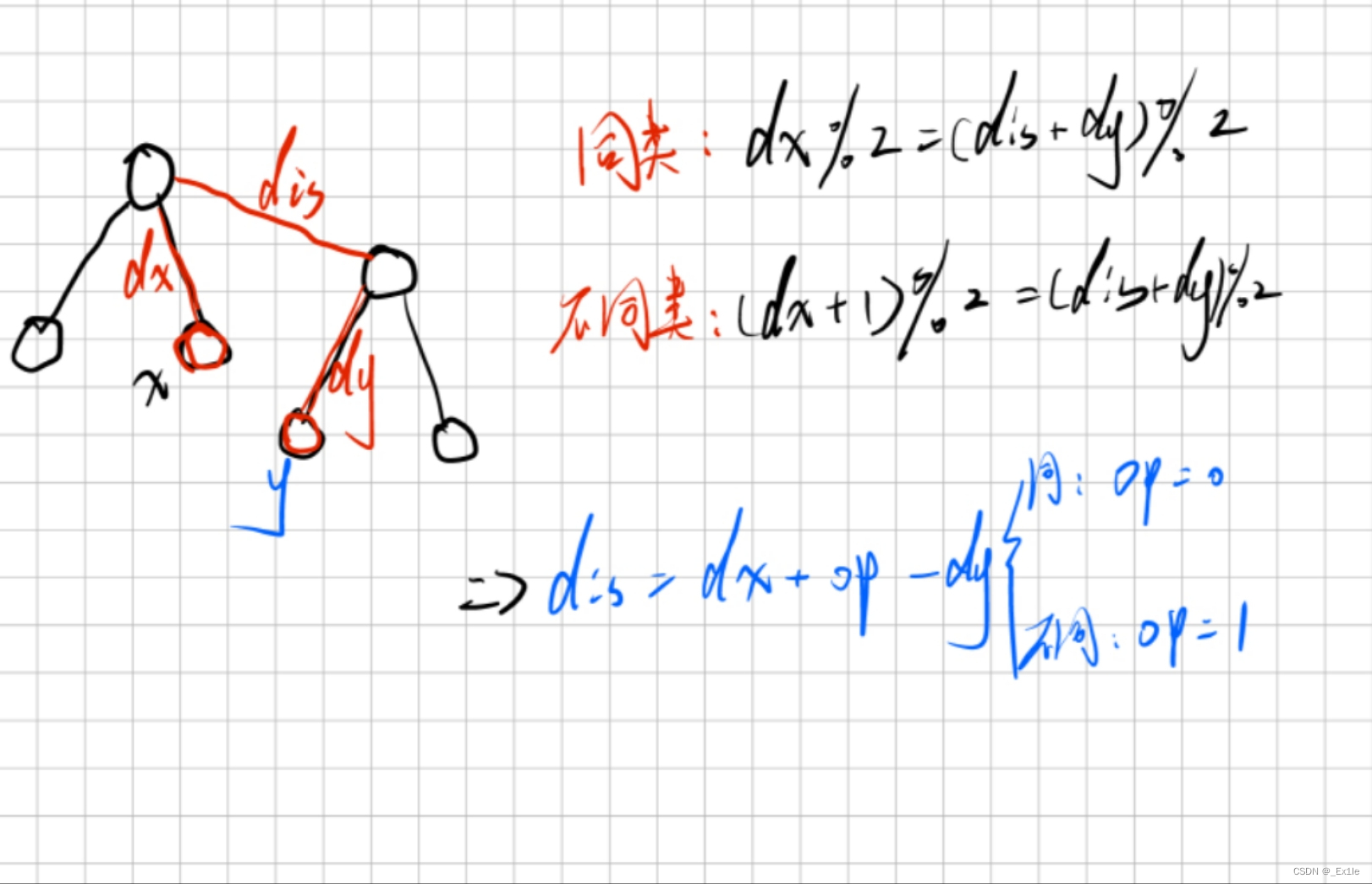
 我们就可以得到压缩路径的公式为，加上的2是一个偏移量为了保证括号内的数为正数。

        那么此时问题就简化为：有若干个集合，每个集合中有两种人，分别从每个集合中选一部分人作为好人，看有没有唯一的一种方式使得好人数是p1的问题。

        例如：集合一有两种人，人数分别为：2，3；集合二有两种人：人数分别为1，5。现在告诉你总共有4个好人，那么显然只能选择集合一中的3和集合二中的1。

        此时问题就是一个背包问题，我们用dp[i][j]来代表从前i个集合中选取j个人作为好人的方案总数。同时如果存在解的情况下我们还要输出具体是哪些人，所以我们还要知道每个集合中两种人具体是哪些人，具体实现代码如下：

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#define pb(x) push_back(x) 
using namespace std ; 
const int N = 1008 ; int prv[N] ;        // father 
int d[N] ;          //到根节点的距离
bool vis[N] ;       //标记这个点有没有用过，用来统计一个集合中有多少元素用的
int cnt[N][2] ;     //cnt[i][0] / cnt[i][1] 分别代表第i个集合中两部分人的个数
std::vector<int> s[N][2] ;  //记录第i个集合中0部分具体是哪些人，1部分具体是哪些人
int dp[N][N] ;      //dp[i][j] 代表从前i个集合中选j个人是好人的方案数
int path[N][N] ;    //path[i][j] 用来记录路径，记录i,j这个状态是由哪个组合传递过来的
int n , p , q ; int find(int x){if(x != prv[x]){int t = prv[x] ;    //带权并查集压缩路径这里一定要先获取fatherprv[x] = find(t) ;  d[x] = (d[x] + d[t]) % 2 ; //压缩路径 }return prv[x] ; 
}void merge(int x , int y , int op){int fx = find(x) , fy = find(y) ; if(fx != fy){prv[fy] = fx ; d[fy] = (d[x] + op - d[y] + 2) % 2 ;    //也是压缩路径,但是要加偏移量保证括号内是正数}
}void init(){for(int i = 1 ; i <= p + q ; i ++){prv[i] = i ; vis[i] = false ; d[i] = cnt[i][0] = cnt[i][1] = 0 ; s[i][0].clear() , s[i][1].clear() ; }
}int main(){while(cin >> n >> p >> q){if(n == 0 && p == 0 && q == 0) break ; init() ; while(n --){int a , b ; string op ; cin >> a >> b >> op ; if(op == "yes"){   //同类merge(a , b , 0) ; }else{merge(a , b , 1) ; }}int count = 0 ; for(int i = 1 ; i <= p + q ; i ++){if(!vis[i]){int t = find(i) ; for(int j = i ; j <= p + q ; j ++){if(t == find(j)){cnt[count + 1][d[j]] ++ ; s[count + 1][d[j]].pb(j) ; vis[j] = true ; }}count ++ ; }}memset(dp , 0 , sizeof dp) ; dp[0][0] = 1 ; for(int i = 1 ; i <= count ; i ++){for(int j = p ; j >= 0 ; j --){if(j >= cnt[i][0] && dp[i - 1][j - cnt[i][0]]){  //如果能选第i个集合的0部分人dp[i][j] += dp[i - 1][j - cnt[i][0]] ; path[i][j] = cnt[i][0] ; }if(j >= cnt[i][1] && dp[i - 1][j - cnt[i][1]]){  //如果能选第i个集合的1部分人dp[i][j] += dp[i - 1][j - cnt[i][1]] ; path[i][j] = cnt[i][1] ; }}}if(dp[count][p] != 1) cout << "no" << '\n' ; else{vector<int>ans ; ans.clear() ; while(count){if(path[count][p] == cnt[count][0]){        //寻找路径p -= cnt[count][0] ; for(int i = 0 ; i < cnt[count][0] ; i ++){ans.pb(s[count][0][i]) ; }}else{p -= cnt[count][1] ; for(int i = 0 ; i < cnt[count][1] ; i ++){ans.pb(s[count][1][i]) ; }}count -- ; }sort(ans.begin() , ans.end()) ; for(int i = 0 ; i < ans.size() ; i ++){cout << ans[i] << '\n' ; }cout << "end" << '\n' ; }}return 0 ; 
}

[水平有限，欢迎指正]