关于十大排序算法联系和递进关系的思考

备战秋招面试，微信搜索公众号【TechGuide】关注更多新鲜好文和互联网大厂的笔经面经。
作者@TechGuide【全网同名】
点赞再看，养成习惯，您动动手指对原创作者意义非凡🤝

前言

小规模的数字排序是一件很容易的事情，学过算数的小盆友都可以轻松应对。但是当数据规模达到一定量级时，如何快速高效的排序就变成了一个富有趣味性的挑战了，往往在大数据量的应用场景中，排序算法才能充分发挥它的威力。

以下内容将会尽全力深入浅出地探讨所有的排序算法。首先，需要明确以下几点：

• 没有任何一种排序算法在所有情况下都是最优的。
• 本文只探讨基于比较的排序，无论是字符或是数字，需要有比较规则。
• 稳定性是指，任意两个相等的数据，排序前后的相对位置不变

排序算法

冒泡排序

每次比较相邻的两个元素，根据比较规则执行交换，每次最大或最小的会换到一边，问题规模由n变为n-1。

以上代码比较简单，这里给出三点说明：

1. flag的作用是为了判断再一趟冒泡排序中是否发生了交换，如果无交换，说明已经排好顺序，就不需要再继续剩下的循环判断了，可以直接结束。
2. 时间复杂度： 最好—O(N) 一开始就已经排好序了，遍历一遍即完成。
   最坏–O(N^2) 完全反序，两次嵌套循环。
3. 优点在于可以适用于链表结构，且稳定。

插入排序

插入排序可以理解为抓牌打牌的过程，对于新到手的牌我们总是一一比较最后找到合适位置，插入即可。同样的道理，插入排序就是这一检验抽象来的排序算法。

时间复杂度和稳定性同冒泡排序。

总结以上两种排序算法，首先给出一个“逆序对”的概念，对于下标i<j,如果A[i] > A[j],则（i,j）即是一对逆序对（inversion）。所以，无论选择排序还是插入排序，都是要消除逆序对的，冒泡排序的一次交换相邻元素刚好消去一个逆序对。插入排序中，如果一个序列基本有序，那么插入排序简单且高效。得出一个重要结论：任何仅以交换两元素来排序的算法，其平均时间复杂度为$\Omega (N^2)$,所以要赶紧算法，每次交换要消除大于一个逆序对。

希尔排序

既然想要一次交换能够消除更多的逆序对，那么我们可以尝试把这个交换的两数的范围增大，这样是可能会一次消除多个逆序对，从而带来更好的算法时间复杂度的，而且保留插入排序的简单性。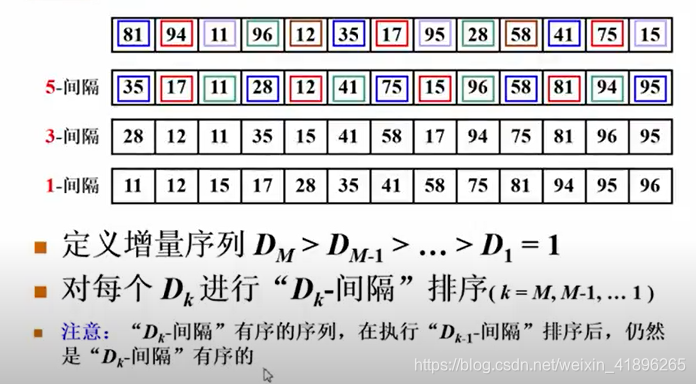
原始希尔排序可以通过以下代码理解。

核心就是对等间隔取的子序列进行插入排序，并且这个间隔会按照增量序列递减直到1为止，这样可以确保完全有效。但是这样的时间复杂度仍然不够理想，如何改进呢？

改进增量序列！

之前一直是取半，这里给出各种（稀奇古怪的增量序列，有兴趣的可以去看看源论文）改进：

选择排序

选择排序的伪代码如下所示，很容易理解：

堆排序

注意，最后一部分代码是把额外空间中的temp值赋回原数组。

归并排序

关于归并排序，要把握住一个核心，即有序子列的归并。

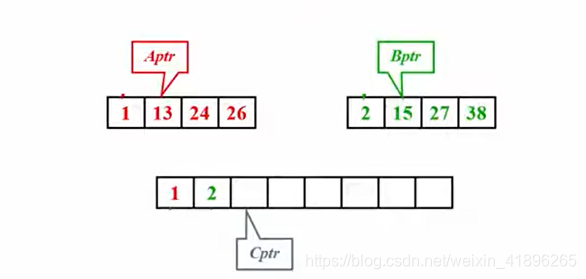
比如上图中A子列和B子列归并为一个大的有序子列，则需要不断移动指针并比较，因为每个元素都要扫一次，所以时间复杂度为$O(N)$。
代码实现思路是，设定两个指针分别指向左右两个待排子序列，比较小的那个可以先移入存放结果的数组，并且指针右移，直到两子序列中有一个全部元素都被扫完，另一个子序列剩余的部分直接移入结果数组即可。注意，最后一步赋值回原数组的小技巧是从右往左赋值，想想为什么不从左往右呢？
伪代码如下：
下面的问题是如何实现上述这种归并思想呢？

1. 不难想到，第一种可以利用分治+递归的算法实现，即把原数组不断切分，处理他的子问题，代码实现如下，注意这里调用了我们上面写好的Merge函数。
   
   时间复杂度可以通过分治经典的递推式推导得到，应该是很符合预期的数字。
   
   可以自己手动推导一下，加深记忆。
   
   注意，任何情况下他在任何情况下都是O(NlgN)，并且是稳定的。（为什么呢？结合上面代码思考一下。）

2. 非递归算法如何实现呢？

思路是每次归并两个长度为length的子序列，length从1开始递增，直到归并成一个结果序列。
请结合下图思考一下他的时间复杂度是多少呢？

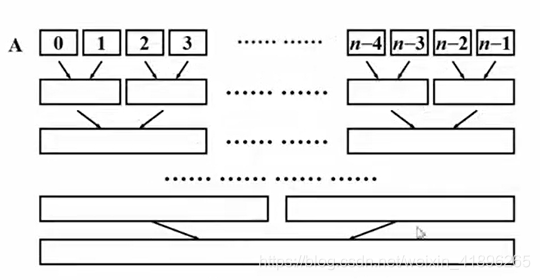
实际这张图有一定的误导性，正确的答案是$O(N)$，因为只需要开出两个长度为N的数组，并且来回赋值即可，仔细思考一下这个过程。
代码实现如下图：

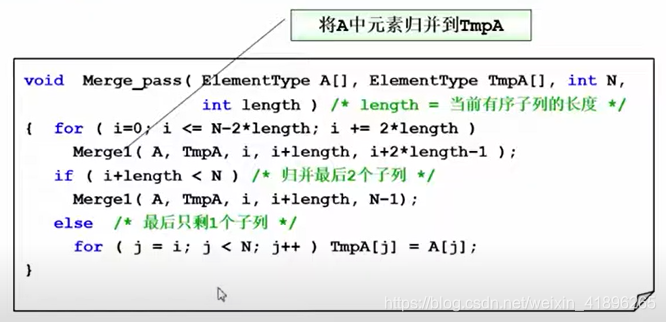
归并排序对外的接口如下：

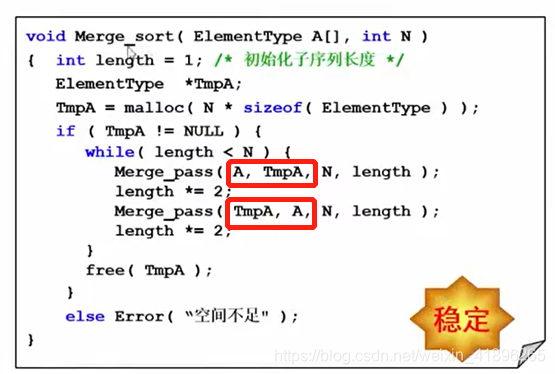
注意红框的部分，实际上就是实现了结果数组的空间和临时数组的空间来回利用的过程。

这里我们就有一个总体感觉了，哎呀，归并不错呀，它的最坏和平均复杂度都是$O(NlgN)$，而且还是稳定的，这不是完美的排序算法吗？但事实是这样吗？对了，他需要一个额外的空间，并且需要数组之间来回复制，所以在内排序中并不常用，多用在外排序。

快速排序

接下来，就是现在最常用、公认最快的排序算法了，没错，就是快排了，关于快速排序，我用对话形式写过一篇比较生动的文章，请大家移步这里。他的思路可以参考下图，这样感觉并不是很复杂，但是他的实现过程中很多值的选取是要十分注意的，一不留神，性能就会大打折扣，具体请看我的那篇关于快排的文章。

这里再总结一下注意点：

1. 这种快排的最好情况是每次正好选到中间的数（中分），时间复杂度为$O(NlgN)$。
2. 如何选主元？可以直接选第一个元素作为pivot吗？这样最坏情况是什么呢？
   不出预料，效果爆炸。如何改进呢？
   没错，这个问题早就有一堆人思考过了，目前最常用的选主元方法是，取头、中、尾三个数的中位数作为主元。代码如下（思考一下，随机取数可以吗？）
   
   思考以上代码最后两行，他的想法是既然知道了中间数比right小了，我何不把它直接放到right的前一位，这样可以省去后续头、尾两个元素比较的开销。
3. 如何做好子集划分呢？

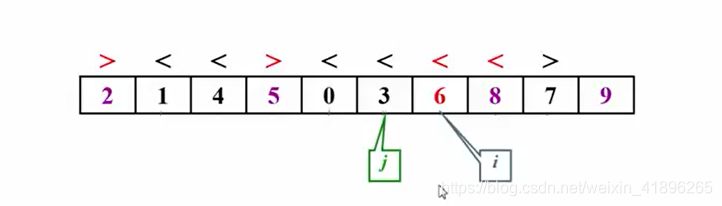
快排的原理这里不再赘述，但是它的核心，也是相较于插入排序的优势就在于，他每次主元每次插入（交换）的位置都是它最终的位置，不需要再移动了，同时，数组被划分为子集。
那么，思考一个细节问题，也是面试官常考察深度的问题。
$$“如果在排序过程中，正好有元素等于主元pivot，应该如何处理呢？”$$
这时候无非两种选择，停下来交换，或者不理睬。
对于第一种方法，考虑极端情况，如果所有数字相等，则会有很多无用的比较交换，但是好处是可以使主元停在中间，时间复杂度可以达到$O(NlgN)$。
对于第二种方法，极端情况避免了无效交换，但是时间复杂度$O(N^2)$.所以，emmm。。你懂的，我们还是选择第一种好了。
快速排序的缺点就在于，他是使用递归的，递归在大规模数据是不够友好的，所以在规模充分小的时候，可以调用简单排序解决问题，比如选择排序。
最后给出代码：

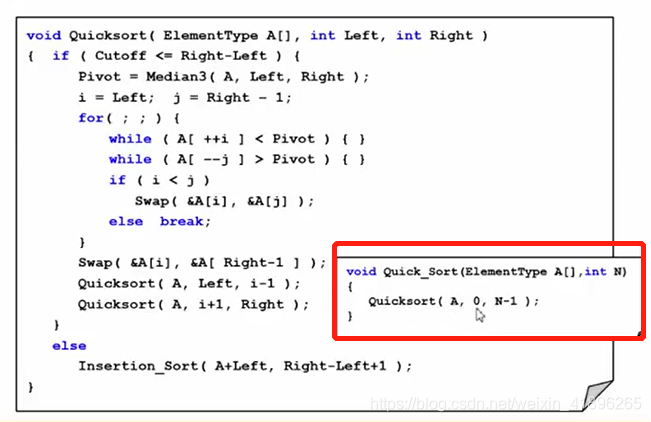
注意，这里的cutoff就是你设置的应该使用选择排序的数据规模阈值，红框中是外部调用的接口。

表排序

思路是，不移动数据（key）本身，而是移动指针（table下标）的排序，是一种间接排序。

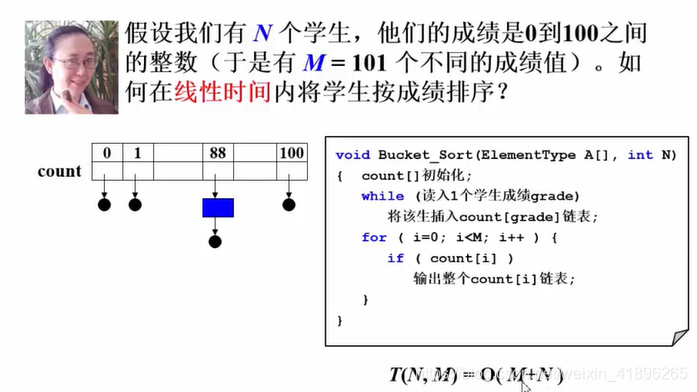
桶排序

仅仅以基于比较大小交换元素的排序，最坏时间复杂度是$O(NlgN)$。所以能不能交换的同时，做点其他的事情呢？（姥姥美颜暴击【笑cry】）

基数排序

基数排序是桶排序的改进版。

P是指扫描次数，为lg（N）级别，如果桶数足够小，可以接近线性时间内排序。

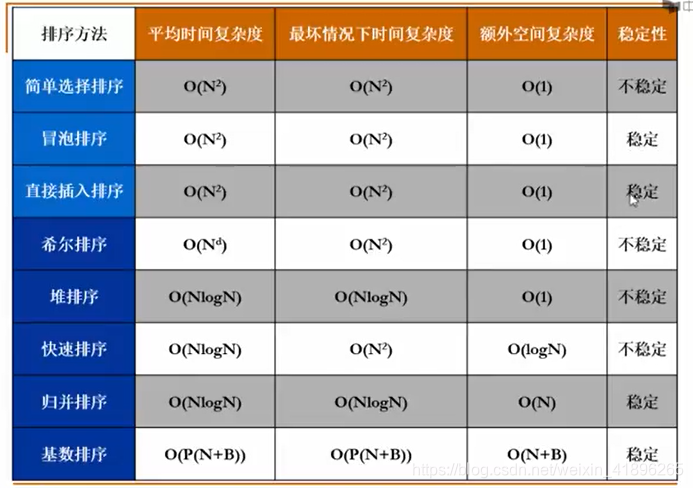
总结

说明：
选择排序不稳定的原因是，跳着交换是可能让相等数序列颠倒的，举个简单的例子,就知道它是否稳定…例如:(7) 2 5 9 3 4 [7] 1…当我们利用直接选择排序算法进行排序时候,(7)和1调换,(7)就跑到了[7]的后面了,原来的次序改变了,这样就不稳定了.。
希尔排序的d取值取决于增量序列的选择。
堆排序和归并排序的平均和最坏都是$O(NlgN)$，但是归并的缺点是需要一个额外的数组空间“倒腾“数组，归并的优点是稳定。
快速排序是不稳定的（跳着交换嘛，不赘述了），但是因为是递归的，所以需要额外的堆栈空间。

说明：
以上所有图片来自于浙大数据结构公开课课件ppt，源地址