他们用深度学习「追星」

文 / Kyle A. Pearson

简介

18 世纪初，物理学家和天文学家急切地想要检验牛顿刚发现的引力定律以及开普勒的行星运动定律。为了检验这些理论的正确性，天文学家 Urbain Le Verrier 和 John Couch Adams 在 18 世纪对天王星展开多次观测。

通过观测，他们发现，天王星的运行轨道与其基于开普勒定律计算得出的结果之间存在偏差。天王星运行时不断加速，然后当其远离木星和土星的引力场时，又会在轨道的某些特定地点减速。两名天文学家提出，天王星所经受的摄动是由太阳系中另一个天体所致。后来发现这个天体是海王星，而在提出此预测之前，人们对海王星一无所知。

检测行星轨道摄动技术也可用于探测新行星或系外行星。然而，匹配数据与摄动模型需要测试数千个 N 体模拟（N-body simulations），方可得出最适合摄动器的参数。现在我们不必使用蛮力法，机器学习可以更高效地估算参数空间中的搜索位置。更广泛的分析（如使用嵌套抽样）可用于生成后验分布，最终获得不确定因素和参数。

此项目是 #PoweredByTF 2.0 Challenge 的一个优胜作品。有关此项目如何使用 TensorFlow 的详细技术描述，请参阅此 论文。下文具体叙述训练数据的过程，并对 TensorFlow 的使用方法进行总结。

注：论文 链接

https://arxiv.org/abs/1907.03377

测量摄动

人们使用地面望远镜与太空望远镜不断搜寻恒星附近的行星（即系外行星），从而寻找宜居行星以及外星文明。

测量系外行星运行轨道的一个方法是凌日法，即长时间观测一颗恒星的亮度，并期冀有行星从其前方经过，从而遮蔽与该行星大小成比例的光亮。其他影响（如旋转恒星上的恒星黑子）也会造成恒星亮度变暗，人们还是认为恒星的周期性亮度变暗源于绕其旋转的行星的遮蔽。

观测勘察器（如开普勒太空望远镜、TESS、WASP）针对数百万颗恒星，搜寻可能表明存在绕其公转行星的周期性信号。 凌日系外行星勘测卫星 (TESS) 展开全宇宙勘察，在太阳系之外寻找与地球大小相似的行星。深度神经网络在筛选这些巨大数据集以寻找行星凌星事件（如 2018 年 Pearson 等人以及 2018 年 Shallue 与 Vanderburg 的发现）方面表现出色。

注：凌日系外行星勘测卫星 链接

https://tess.mit.edu/

发现行星凌星事件后，可从数据中得出一个最佳的光变曲线模型，从而推导 “半程凌星时间 (time of mid-transit)”。“半程凌星” 数值用于推导轨道周期，推导过程中将线性函数拟合至按顺序排列的 “半程凌星” 测量值。根据线性拟合与数据的差异（通常称为是实际观测值与理论计算值差异，O-C），从而测量得出轨道摄动。摄动会造成内部行星加速或减速运转，具体根据摄动天体的位置而定，并且会对运行周期产生几分钟的影响。

注：光变曲线模型 链接

https://ui.adsabs.harvard.edu/abs/2002ApJ...580L.171M/abstract

线性函数 链接

https://github.com/pearsonkyle/Nbody-AI/blob/master/Retrieval.md#linear-ephemeris

训练数据

虽然系外行星勘察任务可在几分钟内测量摄动，但解读测量值则要涉及大量反复的计算工作。计算多行星系统的摄动模型需对时间运动方程求积分。在 N 体模拟中，使用引力计算每个星体的加速情况，然后用于更新每个时间步长 (timestep) 的速度和位置。这种解决方案并非解析函数，并且引力也随位置变化而有所不同，所以需要通过连续时间积分以推导加速变化情况（查看有关特定参数如何影响摄动形状的详情图解）。此项目使用 REBOUND 框架来模拟我们希望通过望远镜而测量的摄动。

注：特定参数如何影响摄动 链接

https://github.com/pearsonkyle/Nbody-AI/blob/master/figures/ttv_parameter_explore_v2.png

当前，探索系外行星是一项热门研究课题，目前已经确认发现 4000 多颗行星，但仅有数百颗行星属于多行星系统，存在能够测量摄动的行星数量则更少。由于现实世界中可用于训练的测量值不够，我们必须基于所预测的结果模拟得出一些示例。可使用下列源代码生成 N 体模拟：

注：源代码 链接

https://github.com/pearsonkyle/Nbody-AI

代码生成如下图所示的输出：

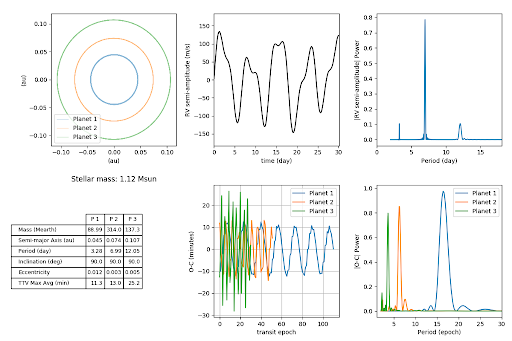
N 体模型需依赖于下列参数：恒星质量 (M*)、内部行星质量 (M1)、内部行星轨道周期 (P1)、外部行星质量 (M2)、外部行星轨道周期 (P2)、外部行星偏心率 (e2) 以及外部行星近星点参数 (w2)。

通常情况下，需要事先已经得知关于恒星和内部行星的参数。因此，使用 TensorFlow 的机器学习算法能够根据给定的已知参数和测量到的摄动（即 O-C 数据）预测得出摄动星体的参数（M2、P2、e2、w2）。此神经网络是一个双重输入、多重输出的回归模型。使用全连接神经网络对独立特征（M*、M1、P1）进行分析，基于时间的特征则需使用卷积神经网络进行分析。每个分支的输出进入全连接神经网络，最终预测出四个参数 （M2、P2、e2、w2）。神经网络架构示例如下所示。

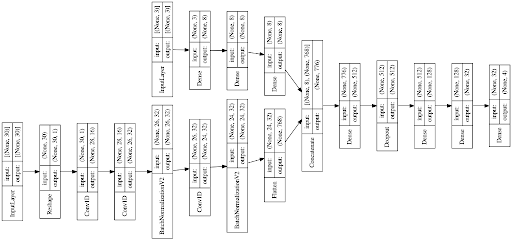
模拟训练数据的目的是优化神经网络，从而处理来自特定望远镜勘察器（如 TESS）的数据。TESS 的使命是展开全宇宙勘察，测量宇宙的部份区域。此过程历时最长为 180 天，最短为 27 天，具体时间则取决于 RA 与 Dec。

注：RA 与 Dec 链接

https://heasarc.gsfc.nasa.gov/docs/tess/operations.html

研究发现，需要至少 20 个凌星测量值才可推导出一个确定的轨道周期。如果我们获得训练数据范围之外的真实数据，就可模拟更多数据并再次进行训练。神经网络经过训练后，误差与敏感度作为轨道周期和相伴行星质量的函数。误差用于估算先验分布，实现更细致的贝叶斯优化，从而推导出行星参数的后验分布（参见图片）。

注：研究 链接

http://adsabs.harvard.edu/abs/2008ApJ...688..636N

图片 链接

https://github.com/pearsonkyle/Nbody-AI/blob/master/Retrieval.md#validation

结论

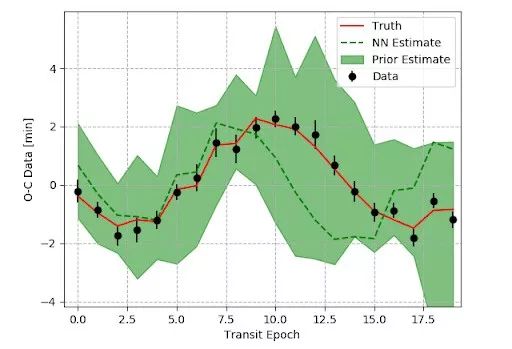
多行星系统中的系外行星由于遭受来自其相伴行星的引力摄动，会引起明显的轨道偏离。这些摄动可用于预测其相伴行星的存在与否和质量大小。分析摄动通过生成数千个 N 体模拟，从而得出与数据最相配的参数集。N 体模型需要对时间运动方程求积分，所以计算量巨大。机器学习用于映射轨道摄动和行星系统参数的相关性，而神经网络预测的不确定因素则被用作贝叶斯检索的先验分布。贝叶斯检索在估算含有另一颗行星的模型与不含其他行星的模型有着重要的意义。如有兴趣研究下源代码，请查看 GitHub (https://github.com/pearsonkyle/Nbody-AI/) 。