拉马努金：我做数学只用三个词，“显然”、“显然”还是“显然”

”拉马努金是整个数学界，甚至可能是整个科学史上最奇怪的人。他如同一颗爆发的超新星，照亮了数学最黑暗、最深刻的角落，然后在 33 岁时不幸被肺结核击倒，就像他的前辈黎曼一样。“

拉马努金被誉为“与神对话”的数学天才。1923 年，数学界发布了一个重要的的消息，有人成功证明了所有足够大的奇数都能写成三个素数之和。而这对于黎曼猜想的破解意义重大，拉马努金对这一方法的发展可谓功不可没。

 黎曼假设，即素数的未解谜题，被视为数学研究的“珠峰”，吸引了一代代数学家投身于数论研究中，其中不乏数学史上大名鼎鼎的人物。拉马努金便是其中之一。

《悠扬的素数：二百年数学绝唱黎曼假设》，[英] 马库斯•杜•索托伊（Marcus du Sautoy）著。

牛津大学数学教授，英国皇家学会研究员马库斯•杜•索托伊科普力作，在黎曼假设这座“数学珠峰”的攀登路上，留下了数学史上大名鼎鼎的人物的足迹。随着计算机的发展和粒子物理学的加入，征服黎曼假设的故事又揭开了新的篇章。

你能解出下面的式子吗？

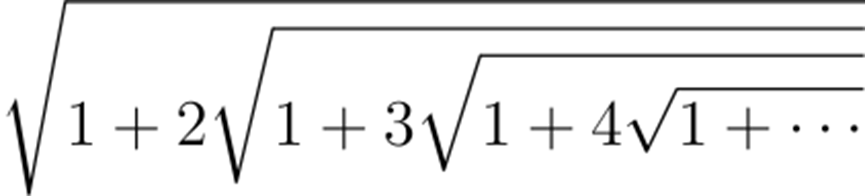
这是1911年拉马努金尚未成名时公开提出的第一个问题。答案会在下面的“数学”章节公布，如果你想试着求一下，记得在滑到那里之前得到答案。

斯里尼瓦萨·拉马努金 (Srinivasa Ramanujan) 是有史以来最伟大的数学家之一。今天的数学家还没能完全理解他的成果。他的工作不仅被应用到数学中，后来还被用到物理学的黑洞和弦论中。

著名数学家小野健（Ken Ono）写道：“拉马努金的智慧甚至比全世界所有顶尖数学家的加起来还要多。”

与拉马努金相识的大数学家林特伍德（J. E. Littlewood）说“所有自然数都是拉马努金的密友”，他仿佛知道每个数字的个性一样。

弗里曼·戴森（Freeman Dyson）这样评价他：“我觉得拉马努金更像莫扎特，在他眼里数学是一门自然而然、显而易见的学问。他的天赋是我们无法理解的奇迹。”

更出名的是这样一则轶事：

著名数学家哈代乘出租车去医院看望拉马努金。为了帮他解闷，哈代告诉拉马努金说，出租车的编号是1729，“一个看起来没什么意思的数字”。拉马努金却说：“不，这是个非常有趣的数字。在所有能用两种方式写成两个自然数立方和的数字中，它是最小的那个。”拉马努金指的是，我们现在把这种数叫做的士数。

尽管拥有非凡的成就，但拉马努金基本上是自学成才，没有接受过正规的数学教育。

他对分析、数论、无限级数和连分数等领域做出了重大贡献，包括解决当时被认为无法解决的数学问题。事实上，人们估计在拉马努金短暂的一生中，他发现了大约3900个有意义的公式！

拉马努金的故事是数学界最伟大的故事之一。通过对薄薄一本书的启发和研究，拉马努金能够提出数千个定理。其中一些是对数学界已经证明和已知的结果的重新发现（他独立推导出了欧拉、高斯等人在他之前发现的许多结果），还有一些是前所未见的新发现。

在这里，我们将尝试了解拉马努金的生平和数学天赋。我们还将看到他的一些惊人成就，直到今天，数学家们还不知道他是如何取得这些成就的。

自学成才的神童

拉马努金小时候就才华出众。

1887年，拉马努金生于印度。全家住在一个传统的小房子里。他的母亲是家庭主妇，有时会去当地寺庙祈诵。大约十岁时，拉马努金以全地区第一的成绩从小学毕业。进入中学后，他第一次接触到了正式的数学。

13岁时，他借到了一本高等三角学的书，掌握了这个领域。这个年纪，他已经独立发现了一些复杂的定理。14岁时，他帮助老师把1200名学生分派给35名老师指导。

在数学考试里，拉马努金只用一半时间就能答完题，并且他对几何和无穷级数也十分熟悉。1902年，拉马努金已经了掌握如何求解三次方程。后来，他发展出了自己独特的四次方程解法。

真正唤醒拉马努金天赋的转折点是在1903年，16岁的拉马努金拿到了一本凯尔（G. S. Carr）的《纯粹和应用数学基本结果概要》。这本书写于1886年，总结了当时已知的绝大多数数学结论。据说拉马努金仔细地研究了这本书里面5000个数学定理。

第二年，拉马努金发现并研究了伯努利数，并将欧拉-马斯切罗尼常数计算到了小数点后15位——这是一项里程碑式的成就。当拉马努金1904年中学毕业时，校长说他是一个应当获得比满分还高的分数的优秀学生。

接下来在大学里，只有数学才能让拉马努金集中注意力。这给他带来了一些麻烦，因为他很难通过其他课程。他最终肄业，也没找到工作。他陷入了极端贫困中，经常食不果腹。然而，他仍然尽一切可能进行独立研究。

当时，拉马努金疾病缠身，到1910年下半年，他已经十分虚弱了。他把笔记本交给一位朋友，并叮嘱朋友，如果自己出现意外，就把笔记本寄给其他数学家。好在拉马努金最终康复并拿回了笔记本。就在同一年，其他数学家逐渐了解了拉马努金的才华。最终，他的一些工作发表在了印度数学会的学报上。

拉马努金与哈代

1913年1月16日，拉马努金向当时第一流的数学家哈代（G. H. Hardy）写了一封信。在信的开头，拉马努金提到自己是自学成才。他写道：“我是一名职员…… 我并未受过大学教育…… 但我正在为自己开辟一条新道路……”

接下来是几页数学推演，其中一些内容之前有人推导过，还有一些不完全正确，但这封信结尾有三个非凡的公式。哈代被这几个公式震惊了，他回信说：

这些公式完全征服了我。我之前从未见过类似的东西……能写下它们的人一定是最顶尖的数学家。这些公式肯定是对的，因为没有人会拥有发明它们的想象力。

——哈代

哈代请同事林特伍德来审读这些论文。林特伍德同样被拉马努金的天才所震惊。在与林特伍德讨论过这些论文后，哈代总结说拉马努金一定是“最优秀的数学家，一个拥有非凡创造力和力量的人”

随后哈代给拉马努金回信，请他来英国学习。但哈代也强调证据的重要性，“很有必要让我看一下你所写断言的证明。”

拉马努金在信中只简单写下了受书启发得到的公式，而完全没有写证明。但对于数学家而言，没有证明的命题并不比猜想更好。他们很快建立了通信联系，拉马努金给哈代寄了更多的数学内容。

仅仅在最初两封信中，拉马努金就给哈代提供了120个定理！哈代不知道的是，拉马努金有厚厚两本记满了漂亮的数学命题的笔记本，其中第二本就有21章。在与林特伍德一起看过笔记本中一部分内容以后，哈代评论说，“只有欧拉和雅克比能与拉马努金并肩。”

拉马努金在剑桥与哈代和林特伍德合作了近五年。尽管拉马努金的天赋肉眼可见，但他们之间的合作并不容易。哈代追求严谨的证明，但拉马努金有着完全不同的信仰，并且十分坚定。他相信女神在梦中赋予他数学直觉。

哈代和拉马努金开始一起证明拉马努金的一些命题。哈代竭尽所能以现代数学的方式教育和指导拉马努金。

一战期间，拉马努金在英国的处境十分困难。他是素食主义者，但几乎买不到蔬菜。作为印度人，他在英国受到了严酷的种族歧视，而且非常孤独（尽管他有无穷多个自然数朋友）。好在，拉马努金最终克服了这些障碍。

1918年5月2日，拉马努金凭借“对椭圆函数及对数论的贡献”当选英国皇家学会会员，他也是皇家学会史上最年轻的会员之一。1918 年 10 月 13 日，他成为第一位当选为剑桥大学三一学院院士的印度人。

拉马努金的数学

每篇介绍拉马努金的文章都会包含一些他的数学成果，所以在这里，我们列出了他的一些发现。但需要强调的是，这篇文章不可能包含他发现的所有公式，因为总共有3900个！

哈代曾说拉马努金的发现异常丰富，而且往往有比最初看上去更丰富的内容。拉马努金的发现还有另一个鲜明的特点，那就是它通常都涉及到很大的数字或者很复杂的表达式，几乎只能用计算机才能计算。当然，在20世纪初，还没有这样的计算机。

事实上，我们并不清楚拉马努金是如何做到的。这是整篇故事里最大的谜团。

拉马努金的π表达式

这部分很有趣，拉马努金发现了1/π的一个新的表达式，这是一个无穷级数。

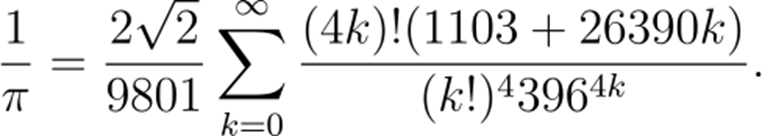
这个级数收敛得极快，现在人们用来计算π的算法就以它为基础。这个级数的第一项就给出了π的前七位有效数字，前两项给出了15位有效数字。事实上，每多计算一项，这个级数就可以多给出8位有效数字！

发散级数

拉马努金研究了无穷发散级数——根据阿贝尔的说法，这是魔鬼的杰作，凡人不可触碰。然而，拉马努金可以给不同的发散求和赋予一些数学意义。其实，一个后来震撼互联网的发散级数就是拉马努金发现的：

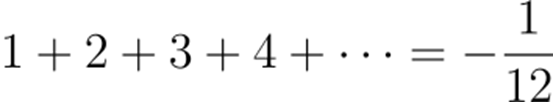
我们可以通过为等号赋予特殊的含义来使这个式子成立。事实上，这样的结果与物理中的一些实验现象吻合，例如两个金属板之间的卡西米尔力。

无穷嵌套平方根

回到印度以后，拉马努金向数学界提出了一项挑战：求出下列无穷嵌套平方根的值。

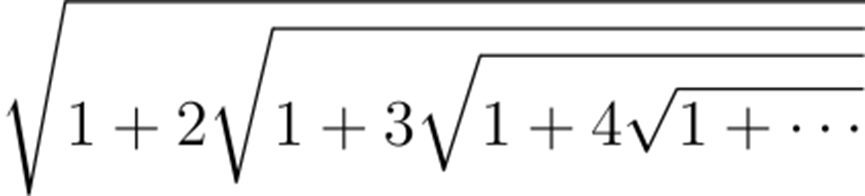
拉马努金等了六个月，但没人能给出答案。于是他直接发表了答案，答案并不复杂，就是3。

几乎是整数

没人知道拉马努金是怎么做到的，但他确实找出了这样几个很接近整数的幂指数：

实际上，上面公式中的平方根通过L函数、椭圆曲线和模形式理论与所谓“类数”相联系。

无限连乘的积分

在寄给哈代的第一封信中，拉马努金在第三页末尾写下了一个逆天的积分：

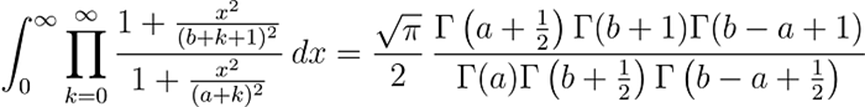
它在0 < a < b + 1/2时成立。

一般来说，把这种倒霉函数连乘再积分，还能得到封闭且美观的解，是一件几乎不可能的事。这实在让人难以相信。

划分数

在集合论中，一个集合分成的一组非空子集叫做划分。对于一个n元集合，不同划分的方式叫做划分数p(n)。

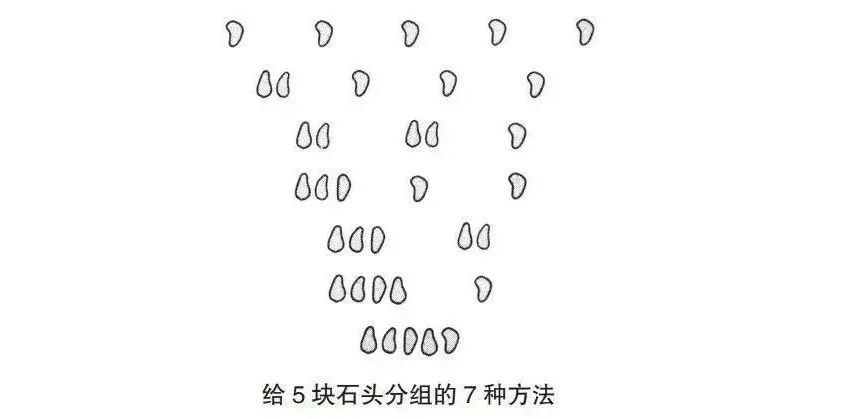
拉马努金推导出了下面这个用于计算划分数的公式

其中，

这个级数的第一项就是p(n)的一个很好的近似，而拉马努金发现

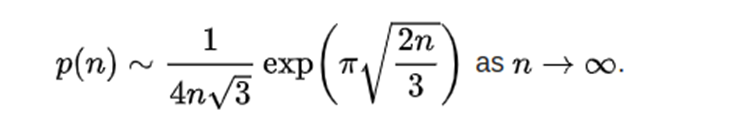
最后的评论

拉马努金的公式优美、巧妙而独特。有些公式如同神迹，直到今天我们仍不知道拉马努金是怎么得到它们的，这是一个巨大的谜团。

拉马努金的成果主要包括：

• 解出了没人觉得有解的上古数学谜题

• 启迪并引领了许多现代数学的研究领域，比如数论中模形式的重要性、韦伊猜想（Weil conjectures）、L函数和朗兰兹纲领（Langlands program）

• 黑洞物理、类θ函数、弦论和量子引力理论等物理理论

拉马努金的身体一直不好，最终不幸病逝于1920年。他临终前的工作后来成为黑洞和弦论等复杂物理理论的数学基础。当然，拉马努金没法想象出黑洞这样的东西，但这洽洽凸显出他强大的直觉和天赋。

著名物理学家加来道雄这样评价拉马努金：“拉马努金是整个数学界，甚至可能是整个科学史上最奇怪的人。他如同一颗爆发的超新星，照亮了数学最黑暗、最深刻的角落，然后在 33 岁时不幸被肺结核击倒，就像他的前辈黎曼一样。”

人们把拉马努金的故事改编成了小说和电影，希望他的故事能继续激励年轻人追求数学——不仅作为一门学科，而且作为一门艺术。

本文经授权转载自微信公众号“中科院物理所”，原文链接：Ramanujan: The Greatest Mathematical。

  推荐阅读

作者：[英] 马库斯•杜•索托伊

译者：柏华元

入围《经济学人》《泰晤士报》《卫报》和《泰晤士报文学增刊》年度好书，知名科普作家卢昌海鼎力推荐 

牛津大学数学教授，英国皇家学会研究员马库斯•杜•索托伊科普力作 

带你一同探索黎曼假设，讲述数学家求知路上的苦与乐