本文主要是介绍10 MIT线性代数-四个基本子空间 four fundamental subspaces,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 四个子空间 Four subspaces (mxn)
列空间 Column space C(A) in
零空间Nullspace N(A) in
行空间Row space = all combs of rows = all combs of columns of AT= C(AT) in
左零空间Left nullspace = Nullspace of AT = N(AT) = left nullspace of A in
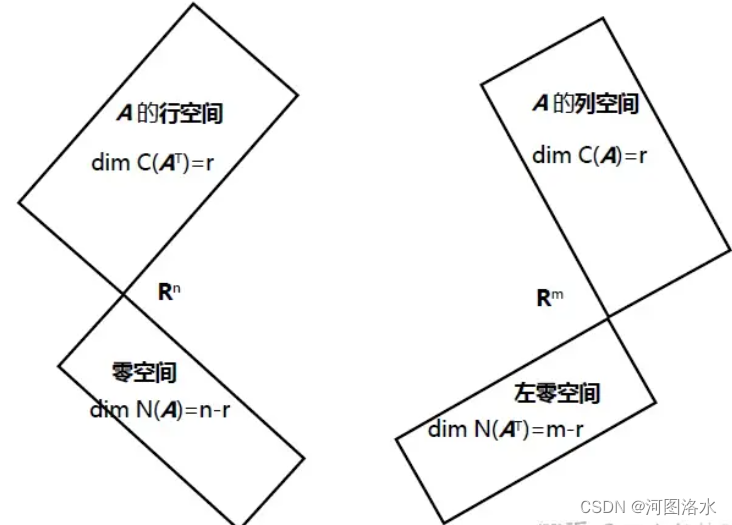
2. 基和维数 Basis& Dimension
列空间 dim C(A)=r
零空间 dim N(A)=n-r
行空间

different col space but same row space
R的前r行阶梯型“行向量”就是矩阵A行空间C( AT )的一组基
Basis for row space is first r rows of R
左零空间 dim N(AT) = m-r

为找到左零空间的基,我们应用增广矩阵 ![]()
EA=R in chap. 2, R was I, Then E was

则矩阵E最下面的m-r个行向量使得矩阵A的行向量线性组合成为0
矩阵E的这m-r个行向量满足yTA=0,它组成了矩阵A左零空间的一组基
3. 新向量空间 New vector space
All 3x3矩阵构成的集合是一个向量空间,符合对于线性运算封闭,称之为M A+B, CA
subspace of M:
upper triangular 上三角阵
symmetric matrices 对称阵
diagonal matrices 对角阵 对角阵是前两个子空间的交集,其维数为3,具有以下一组基

概念延伸
这篇关于10 MIT线性代数-四个基本子空间 four fundamental subspaces的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




