本文主要是介绍每日一题(12)——计算Slim Span(并查集),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
首先总结一下并查集:

其中按秩合并分为:按树的深度和树的大小合并,效果都相同。




问题ID:POJ3522
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 5098 | Accepted: 2671 |
Description
Given an undirected weighted graph G, you should find one of spanning trees specified as follows.
The graph G is an ordered pair (V, E), where V is a set of vertices {v1,v2, …,vn} andE is a set of undirected edges {e1,e2, …,em}. Each edgee ∈ E has its weightw(e).
A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices withn − 1 edges. The slimness of a spanning treeT is defined as the difference between the largest weight and the smallest weight among then − 1 edges ofT.
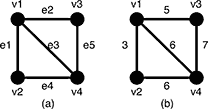
Figure 5: A graph G and the weights of the edges
For example, a graph G in Figure 5(a) has four vertices {v1,v2,v3,v4} and five undirected edges {e1,e2,e3,e4,e5}. The weights of the edges arew(e1) = 3,w(e2) = 5,w(e3) = 6,w(e4) = 6,w(e5) = 7 as shown in Figure 5(b).
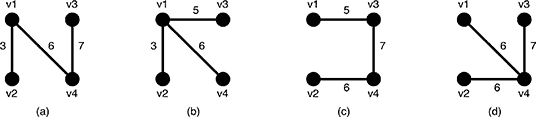
Figure 6: Examples of the spanning trees of G
There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning treeTa in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the treeTa is 4. The slimnesses of spanning treesTb,Tc andTd shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.
Your job is to write a program that computes the smallest slimness.
Input
The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.
| n | m | |
| a1 | b1 | w1 |
| ⋮ | ||
| am | bm | wm |
Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤n ≤ 100 and 0 ≤m ≤n(n − 1)/2.ak andbk (k = 1, …,m) are positive integers less than or equal ton, which represent the two verticesvak andvbk connected by thekth edgeek.wk is a positive integer less than or equal to 10000, which indicates the weight ofek. You can assume that the graphG = (V,E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).
Output
For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters.
Sample Input
4 5 1 2 3 1 3 5 1 4 6 2 4 6 3 4 7 4 6 1 2 10 1 3 100 1 4 90 2 3 20 2 4 80 3 4 40 2 1 1 2 1 3 0 3 1 1 2 1 3 3 1 2 2 2 3 5 1 3 6 5 10 1 2 110 1 3 120 1 4 130 1 5 120 2 3 110 2 4 120 2 5 130 3 4 120 3 5 110 4 5 120 5 10 1 2 9384 1 3 887 1 4 2778 1 5 6916 2 3 7794 2 4 8336 2 5 5387 3 4 493 3 5 6650 4 5 1422 5 8 1 2 1 2 3 100 3 4 100 4 5 100 1 5 50 2 5 50 3 5 50 4 1 150 0 0
Sample Output
1 20 0 -1 -1 1 0 1686 50
此题对kruskal算法做了变形,不是求最小生成树,而是求最大边权值与最小边权值之差最小的生成树,同样可以用kruskal算法的实现方法,采用并查集。如果求最小生成树要将边加入到堆中,并且不需要遍历所有的生成树情况
//此题对kruskal算法做了变形,不是求最小生成树
//而是求最大边权值与最小边权值之差最小的生成树
//同样可以用kruskal算法的实现方法,采用并查集
#include <iostream>
#include <stdlib.h>
#include <algorithm>
#define inf 10000000//边权值的上界;
using namespace std;
int m,n;
//p数组用于记录父节点,r数组用于统计以r为根的子
//树中间有多少个点,其实r数组可以取消,因为
//直接由根节点的绝对值就可以这个集合中的元素个数;
int p[105];
int r[105];
struct edge{
int u;
int v;
int w;
}e[5000];
bool cmp(const edge & e1,const edge & e2){
return e1.w < e2.w;
}
void set_init(){ //并查集初始化;
for (int i = 1;i <= n;i++)
{
p[i] = i;
r[i] = 1;//初始状态每个的根是自己,集合个数为1
}
}
// int set_find(int x){//查找包含x的集合树的根
// while (p[x] >= 0)
// {
// x = p[x];
// }
// return x;
// }
//以上为非递归实现,递归实现如下
int set_find(int x){
if(p[x] == x) return x;
else p[x] = set_find(p[x]);
return p[x];
}
// void set_union(int root1,int root2){//将两个集合合并
// p[root1]+=p[root2];
// p[root2] = root1;//用根root2连接到root1下面
// }
//为防止树的退化,改进版的union操作如下
void set_union(int x,int y){//将两个集合合并
if(r[x] <= r[y]){
p[x] = y;
r[y]+=r[x];//y作为根
}
else {
p[y] = x;
r[x]+=r[y];
}
}
int main(){
int i,j,k,ans,px,py,a,b,temp;
while (cin>>n>>m)
{
if (n == 0 && m == 0)
break;
for (i = 0;i < m;i++)
{
cin>>e[i].u>>e[i].v>>e[i].w;
}
if ( n == 2 && m == 1)
{
cout<<"0"<<endl;//2点1边的情况单独处理
continue;
}
sort(e,e+m,cmp);
ans = inf;
for (i = 0; i<m;i++)
{
k = 0;
set_init();
for (j = i;j<m;j++)
{
px = set_find(e[j].u);
py = set_find(e[j].v);
if (px != py)
{
set_union(px,py);//注意这里只是求生成树,不一定是mst,只要不在同一个集合中就可以选这条边,两个端点变成同一个集合内
k++;
if(k == 1){//这是最小的边
a = e[j].w;
}
else if (k == n-1)//这是最大的边也是最后一条边
{
b = e[j].w;
temp = b - a;
if (temp < ans)
{
ans = temp;
}
break;
}
}
}
}
if (ans == inf)
{
cout<<"-1"<<endl;
}
else cout<<ans<<endl;
}
return 0;
}
这篇关于每日一题(12)——计算Slim Span(并查集)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






