[光学]FP干涉仪的光谱特性及应用

[光学]FP干涉仪的光谱特性及应用研究

（一）基本原理

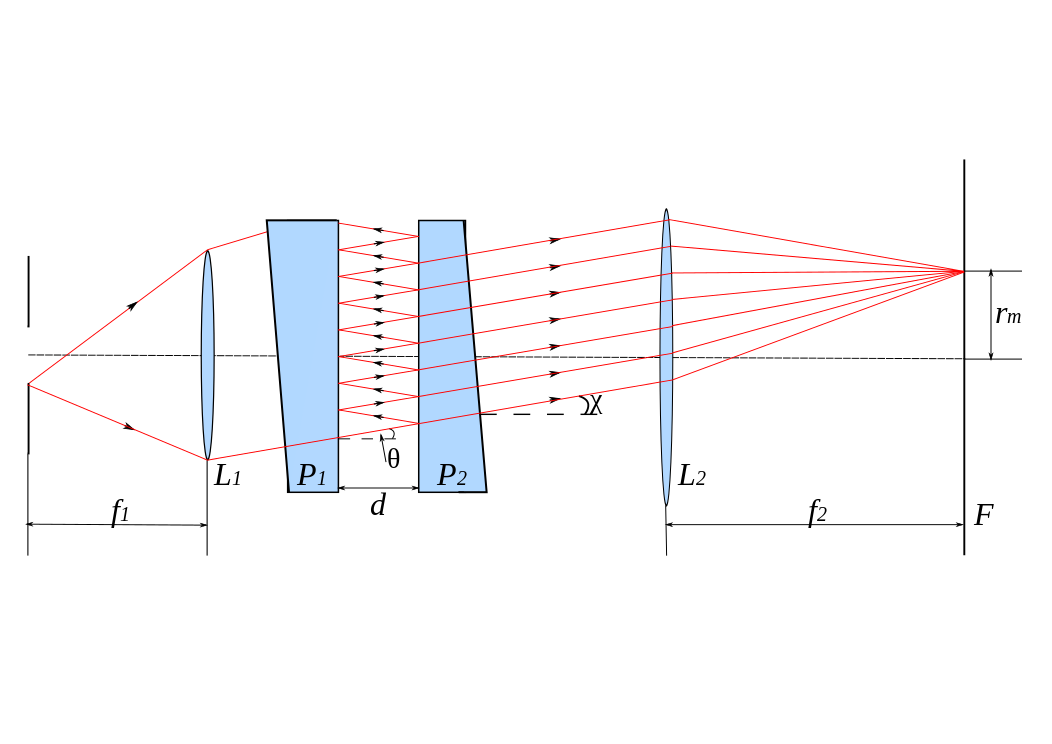
  对称F-P干涉仪原理图
对称F－P干涉仪两侧平板外侧镀有增透膜，可认为透射率为100%。因此，讨论透射光的光振幅变化，各次反射后
透射光光强变化：

ItIi=(1−R)2(1−R)2+4Rsin2δ2

$$\frac{{{I}_{t}}}{{{I}_{i}}}=\frac{{{\left( 1-R \right)}^{2}}}{{{\left( 1-R \right)}^{2}}+4R{{\sin }^{2}}\frac{\delta }{2}}$$

下面通过MATLAB编程研究以上关系

（二）核心代码

%% FP干涉仪-对称
clc,clear
%% 计算式
% delta=4*pi*n*h/lamda;                                         %相位差
syms delta R 
AR=@(delta,R)(1-exp(1i*delta))*sqrt(R)./(1-R*exp(1i*delta));        %反射系数
AT=@(delta,R)(1-R)./(1-R*exp(i*delta));                        %透射系数
F=@(R)4*R./(1-R).^2;                                          %精细度系数
ddelta=@(R)2*(1-R)./sqrt(R);                                    %位相半宽度
S=@(R)pi*sqrt(R)./(1-R);                                        %精细度
%% FP干涉仪参数设定
R1=[0.1,0.3,0.7,0.9];                                           %反射率
R2=0:0.01:1;                                                    %反射率
colors='cmbkryg';                                               %颜色
delta=[1.5*pi:0.001:4.5*pi];                                    %相位差
%% 反射透射光计算绘图
for i=1:4;
Ar=AR(delta,R1(i));
At=AT(delta,R1(i));
Ir=Ar.*conj(Ar);
It=At.*conj(At);
check=Ir+It;
%反射光
figure(1)
subplot(2,1,1)
hold on
plot(delta,Ir,colors(i),'LineWidth',1.5)
subplot(2,1,2)
hold on
plot(delta,angle(Ar),colors(i),'LineWidth',1.5)
if i==4;
subplot(2,1,1)
hold on
title('反射光幅度')
xlabel('位相\delta')
ylabel('Ir/Io')
legend(['R=',num2str(R1(1))],['R=',num2str(R1(2))],['R=',num2str(R1(3))],['R=',num2str(R1(4))]);
axis([1.5*pi,4.5*pi,0,1]);
grid on
subplot(2,1,2)
hold on
title('反射光相位')
xlabel('位相\delta')
ylabel('Ar/Ao')
legend(['R=',num2str(R1(1))],['R=',num2str(R1(2))],['R=',num2str(R1(3))],['R=',num2str(R1(4))]);
axis([1.5*pi,4.5*pi,-1.6,1.6]);
grid on
end
%透射光
figure(2)
subplot(2,1,1)
hold on
plot(delta,It,colors(i),'LineWidth',1.5)
subplot(2,1,2)
hold on
plot(delta,angle(At),colors(i),'LineWidth',1.5)
grid on
if i==4;
subplot(2,1,1)
hold on
title('透射光幅度')
xlabel('位相\delta')
ylabel('It/Io')
legend(['R=',num2str(R1(1))],['R=',num2str(R1(2))],['R=',num2str(R1(3))],['R=',num2str(R1(4))]);
axis([1.5*pi,4.5*pi,0,1]);
grid on
subplot(2,1,2)
hold on
title('透射光相位')
xlabel('位相\delta')
ylabel('At/Ao')
legend(['R=',num2str(R1(1))],['R=',num2str(R1(2))],['R=',num2str(R1(3))],['R=',num2str(R1(4))]);
axis([1.5*pi,4.5*pi,-1.5,1.5]);
grid on
end
end
%% 位相差半宽度精细度系数计算绘图
Fplot=F(R2);
ddeltaplot=ddelta(R2);
Splot=S(R2);
figure
plot(R2,Fplot,'LineWidth',1.5)
title('精细度系数-反射率曲线')
xlabel('反射率R')
ylabel('精细度系数F')
grid on
figure
plot(R2,ddeltaplot,'LineWidth',1.5)
title('位相半宽度-反射率曲线')
xlabel('反射率R')
ylabel('位相半宽度\delta')
grid on
figure
plot(R2,Splot,'LineWidth',1.5)
title('精细度-反射率曲线')
xlabel('反射率R')
ylabel('精细度S')
grid on 

（三）光强随位相变化

  作出透射光强、反射光强变化随位相变化的曲线：

透射光：

• 显然透射光在 对应波长附近时，有明显的透过峰，峰值波长透过率始终为1；
• 其他部分透过率均较小；
• 且随着R的增大，透过峰的锐度越大，允许透过的波长范围越窄不允许透过波长的透过率更小。

反射光：

• 反射光光强变化恰与透射光相反，在 对应波长附近反射光反射率极小，谷值波长透过率始终为0；
• 其他部分有反射光，且随着R的增大，允许反射的波长范围越宽，允许反射波长的透过率更大。