多种群遗传算法的函数寻优算法

多种群遗传算法的介绍

传统的遗传算法是一种借鉴于生物界自然选择和进化机制发展起来的高度并行、随机、自适应的全局优化概率搜索算法。因为优化时不依赖于梯度，具有很强的鲁棒性和全局搜索能力。但是未成熟收敛确实遗传算法中不可忽视的现象，它主要表现为所有个体都区域同一状态而停止进化。

接下来所介绍的多种群遗传算法可以很好地解决这个问题。

多种群遗传算法主要引入了这几个概念。
1.突破SGA仅靠单个种群进行遗传进化的框架，引入多个种群进行全局搜索，不同种群用不同参数，实现不同的搜索目的。2.各种群之间通过移民算子进行联系，实现了多种群协同进化，最优解是多个种群共同进化的结果，3.通过人工算子保留每代中的最优个体，并作为判断收敛的依据。

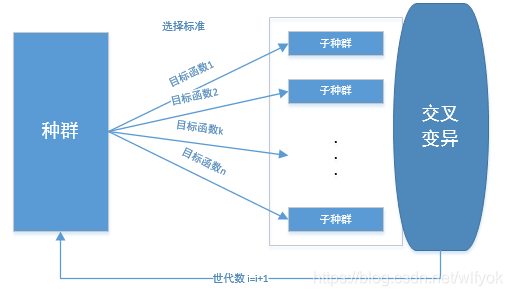
问题与思路

这里是谢尔德工具箱的下载地址，大家可以自行前往gatbx

代码

话不多说，看Matlab代码：

% 多种群遗传算法主函数
clear
clc
nind = 40;
nvar = 1;
preci = 20;
ggap = 0.9;     % 代沟
mp = 10;    % 种群数目
field = [preci;0;1;1;0;1;1];    % 区域描述器
for i = 1:mpchrom{i} = crtbp(nind,nvar*preci);
end
gen = 0;
pc = 0.7 + (0.9-0.7)*rand(mp,1);
pm = 0.001 + (0.05-0.001)*rand(mp,1);
gen0 = 0;
maxgen = 10;
maxy = 0;   % 最优值
% 计算各初始种群的适应度
for i = 1:mpobjv{i} = objf(bs2rv(chrom{i},field));
end
maxobjv = zeros(mp,1);      % 记录精华种群
maxchrom = zeros(mp,preci*nvar);        % 记录精华种群的二进制编码
while gen0 < maxgengen = gen + 1;for i = 1:mp% 各种群的适应度fitnv{i} = ranking(-objv{i});% 选择selch{i} = select('sus',chrom{i},fitnv{i},ggap);% 交叉selch{i} = recombin('xovsp',selch{i},pc(i));% 变异selch{i} = mut(selch{i},pm(i));% 计算子代目标值objvesl = objf(bs2rv(selch{i},field));% 重插入工作[chrom{i},objv{i}] = reins(chrom{i},selch{i},1,1,objv{i},objvesl);end% 移民操作[chrom,objv] = immigrant(chrom,objv);% 人工选择精华种群[maxobjv,maxchrom] = elite(chrom,objv,maxobjv,maxchrom);yy(gen) = max(maxobjv);if yy(gen) > maxymaxy = yy(gen);gen0 = 0;elsegen0 = gen0 + 1;end
end
% 画图
plot(1:gen,yy)
xlabel('进化代数')
ylabel('最优解变化')
title('进化过程')
xlim([1,gen])
% 输出最优解
[y,i] = max(maxobjv);
x = bs2rv(maxchrom(i,:),field);
disp(['最优值为：',num2str(y)])
disp(['对应的自变量取值为：',num2str(x)])function obj = objf(x)
% 目标函数
[row,~] = size(x);
for i = 1:rowobj(i,1) = exp(((x(i,1)-0.1)/0.8)^2)*(sin(5*pi*x(i,1)))^6;
end

这里是谢尔德工具箱的下载地址，大家可以自行前往gatbx

结果显示

可以见到，多种群遗传算法对于函数寻优的效果很好，很快就得到收敛找到最优值。相较于传统的遗传算法，一般问题都需要几十代或几百代来说，效果非常好。