MatLab使用显/隐式Adams求解ODE问题

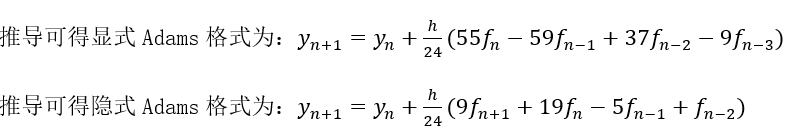
代码：

function example_Adam
T = 1;
h = 0.1;
t = 0:h:T;
N = length(t)-1;
solu = exp(-5.0*t);
u0 = 1;
f = @f1;
u_euler = euler(f,u0,t,h,N);
u_out_Adams = out_Adams(f,u0,t,h,N);
u_in_Adams = in_Adams(f,u0,t,h,N);figure (1)
plot(t,u_out_Adams,'*r',t,solu,t,u_in_Adams,'o');
legend('显示Adams外插','精确解','隐式Adams内插');
end
function u = euler(f,u0,t,h,N)
u    = zeros(N+1,1);
u(1) = u0;
for n = 1:Nfn     = f(t(n),u(n));u(n+1) = u(n)+h*fn;
end end
function u = out_Adams(f, u0, t, h ,N)
u=zeros(N+1,1);
u(1)=u0;
u = euler(f,u0,t,h,4);
for n=4:Nf1 = f(t(n),u(n));f2 = f(t(n-1),u(n-1));f3 = f(t(n-2),u(n-2));f4 = f(t(n-3),u(n-3));u(n+1) = u(n)+(h/24)*(55*f1-59*f2+37*f3-9*f4);
end
end
function u = in_Adams(f, u0, t, h ,N)
u    = zeros(N+1,1);
u(1) = u0;
u = euler(f,u0,t,h,3);
eps_in = 1e-6;K_in = 6;
for n = 3:Ns1 = u(n);du = 1;k  = 1; f2 = f(t(n),u(n));f3 = f(t(n-1),u(n-1));f4 = f(t(n-2),u(n-2));while abs(du)>eps_in && k<K_inf1 = f(t(n+1),s1);s2 = u(n)+(h/24)*(9*f1+19*f2-5*f3+f4);du = s2-s1;s1 = s2;k = k+1; endu(n+1) = s2;
end end
function f =f1(t,u)
f = -5*u;end

结果如下:（采取三种步长)

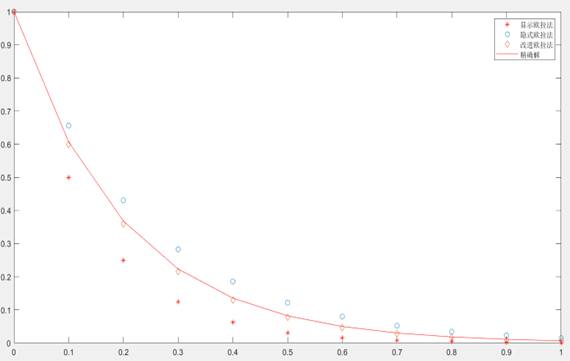
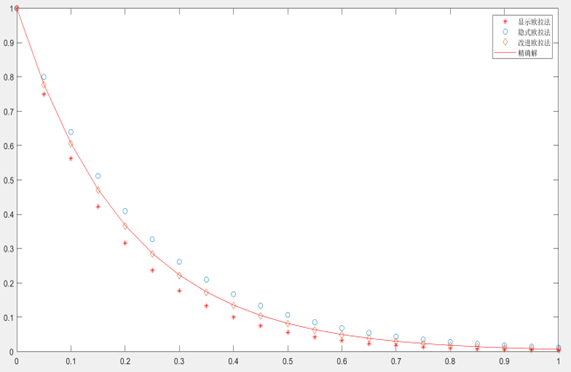
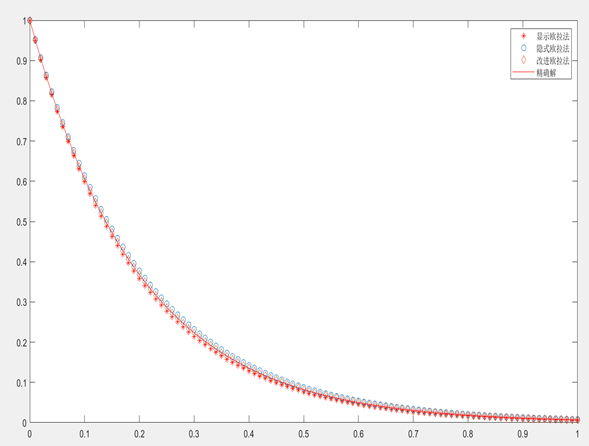
在h变小的过程中，显式Adams算法和隐式Adams算法的精度逐渐升高，接近于精确解。由上图可知隐式Adams法比显式Adams法的更精确，两种算法精度之间的差距随着步长h减小而逐渐减少，注意到在h=0.01时二者结果近乎重合。