本文主要是介绍如果x分钟过去了,我还没有拿到我的行李箱,那么它“上”了飞机的概率是多少?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《The book of why》里的一个问题:
行李箱出现在传送带上有两个因。
第一,它必须一开始就跟随你“上”了飞机上,否则它就肯定不会出现在传送带上。
第二,只要行李箱的确“上”了飞机,那么随着时间的推移,它出现在传送带上的可能性就会越来越大。
同时假设你的行李箱跟随你“上”了飞机的可能性,P(行李箱“上”了飞机=真)为50%。
如果你的行李箱确实“上”了飞机,那么它在第一分钟被卸下来的概率是10%,在第二分钟被卸下来的概率也是10%,以此类推。因此在等待了5分钟后,你的行李箱有50%的概率已被卸下来,也就是P(行李箱在传送带上=真|行李箱“上”了飞机=真,等待时间=5)为50%。10分钟后,所有的行李箱都被卸下来了,所以P(行李箱在传送带上=真|行李箱“上”了飞机=真,等待时间=10)为100%
问题详情可以看webppl概率编程系列(二)
根据多变量条件概率公式的推导(多变量贝叶斯公式)得到公式
P ( X ∣ Y ) = P ( X Y ) P ( Y ) = P ( Y ∣ X ) × P ( X ) P ( Y ) 令 X = A , Y = B C 得到 P ( A ∣ B C ) = P ( B C ∣ A ) × P ( A ) P ( B C ) P(X \mid Y)=\frac{P(XY)}{P(Y)}=\frac{P(Y \mid X) × P(X)}{P(Y)}\\ \text{令}X = A,Y=BC\\ \text{得到}P(A \mid BC)=\frac{P(BC \mid A) × P(A)}{P(BC)} P(X∣Y)=P(Y)P(XY)=P(Y)P(Y∣X)×P(X)令X=A,Y=BC得到P(A∣BC)=P(BC)P(BC∣A)×P(A)
以求如果1分钟过去了,我还没有拿到我的行李箱,那么它“上”了飞机的概率是多少?为例,则
A = 行李上飞机 B = 1分钟 C = 行李没出现在传送带上 A = \text{行李上飞机}\\ B = \text{1分钟}\\ C = \text{行李没出现在传送带上} A=行李上飞机B=1分钟C=行李没出现在传送带上
而 P ( A ) = 0.5 , P ( B C ) P(A)=0.5,P(BC) P(A)=0.5,P(BC)代表行李没在1分钟出现在传送带上的概率,表现为表格的两行:
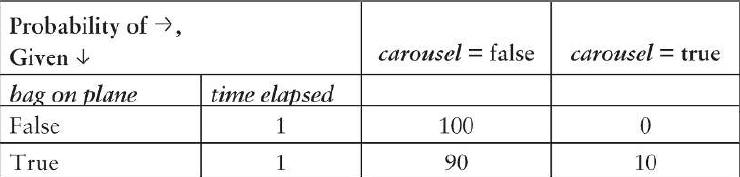
求得 P ( B C ) = 100 + 90 100 + 100 = 0.95 P(BC)=\frac{100+90}{100+100}=0.95 P(BC)=100+100100+90=0.95 .而 P ( B C ∣ A ) P(BC \mid A) P(BC∣A)代表行李上了飞机但没在1分钟出现在传送带上的概率,表现为表格的一行,得到 P ( B C ∣ A ) = 0.9 P(BC \mid A)=0.9 P(BC∣A)=0.9
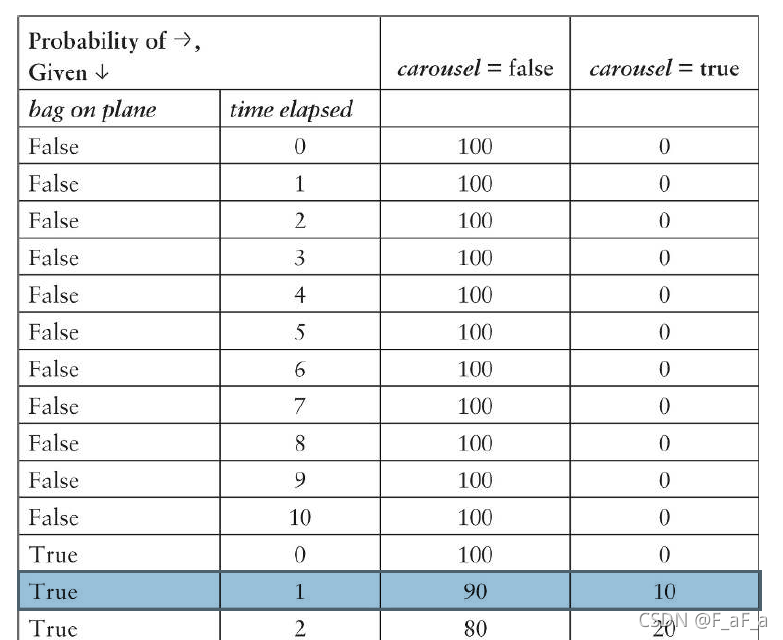
所以最终结果为
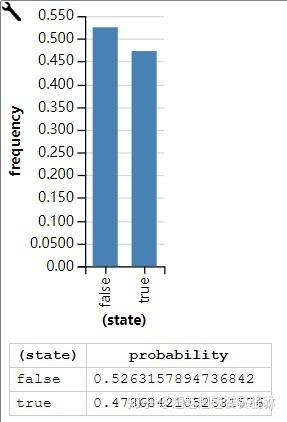
P ( A ∣ B C ) = P ( B C ∣ A ) × P ( A ) P ( B C ) = 0.9 × 0.5 0.95 = 0.4736842105263158 P(A \mid BC)=\frac{P(BC \mid A) × P(A)}{P(BC)}=\frac{0.9× 0.5}{0.95}=0.4736842105263158 P(A∣BC)=P(BC)P(BC∣A)×P(A)=0.950.9×0.5=0.4736842105263158
和图片结果一致
这篇关于如果x分钟过去了,我还没有拿到我的行李箱,那么它“上”了飞机的概率是多少?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






