站在巨人的肩膀上——计算导论

计算导论

计算机的基本原理

从数学危机到图灵机：

• 第一次数学危机：毕达哥拉斯学派认为，“一切数均可表示为整数或整数之比”，但是发现存在一些数，它不是整数，也不可用整数之比表示，希帕索斯提出：边长为1的正方形其对角线是多长呢？这一问题引发了第一次数学危机(希帕索斯悖论)
• 第一次数学危机的解决：实数理论建立后
• 第二次数学危机：牛顿和莱布尼茨发现了微积分，其理论建立在无穷小的分析之上。贝克莱悖论（无穷小时而为0，时而不为0）。
• 第二次数学危机的缓解：在实数理论的基础上重建了极限论
• 第三次数学危机：康托尔创立了集合论，罗素提出理发师悖论。引起思考：是否存在一个完备的系统，从而建立整个数学大厦？哥德尔提出不完备性定理，该定理结束了关于数学基础的争论，宣告了把数学彻底形式化的愿望是不可能实现的。虽然不存在完备的系统，但是，可证真问题和既不可证真也不可证伪的边界在哪呢？这便是可计算问题，那么，如何判断一个问题是可计算问题还是不可计算问题呢？一个研究思路是：模型法。图灵提出了这样一个模型（图灵机）

关于图灵机:

图灵机的构成：存储带、控制器（包含读写头）
图灵机的工作机理：初始化，反复执行下列操作直到停机（读出存储带上的字符，根据当前状态和读取到的字符，找到相应的程序语句，根据相应程序语句，做三个动作，写入、改变状态、移动）
图灵机的意义：对于一个问题A，如果能找到一个图灵机，得出对应的符号序列B，那么从A到B就是可计算的，否则，该问题不可计算。
图灵机的理论意义：给出了一个通用的计算模型，引入了通过“读写符合-改变状态”进行计算的思想

计算机为什么能计算？

回答这个问题，需要解决三个问题：

• 数在计算机中是如何表示的？

  二进制（十进制转二进制：除2取余法）

• 逻辑上数是如何计算的？

  布尔代数。对于加法，本位可由异或产生，进位由与运算产生。

• 物理上数的计算是如何实习的？

  因为参与运算的数可以转换位二进制数，二进制数运算可以运用基本的布尔运算实现，基本的布尔运算都可以由电路实现，因此，电路能算数

计算机的发展趋势

略

程序运行的基本原理

计算机为什么能计算？用二进制表示数据、用布尔代数进行运算、用电路实现布尔运算，故电路可进行计算

冯诺依曼式计算机

冯诺依曼的思路：通过指令控制计算机
冯诺依曼式计算机组成：控制器、运算器、存储器、输入设备、输出设备

存储器种类及特点

• 寄存器

  CPU内部，用于存放待操作数和结果。工作速度与CPU运算部件节拍一致

• 高速缓存（Cache）

  通常在CPU内部，用做数据缓冲区。CPU内部的叫内部高速缓存，主板上的缓存叫外部高速缓存

• 内存

  CPU里想放但放不下的部分

• 外存

以上，形成分层次存储体系。CPU读取数据时，先从缓存中查找，找到则立即读取，否则从内存中读取并送到CPU处理，同时把这个数据所在的数据块调入缓存

CPU对数据的访问：局部性原理（时间局部性和空间局部性）

存储器的原理与类型

存储一位的电路：静态RAM的六管基本存储单元

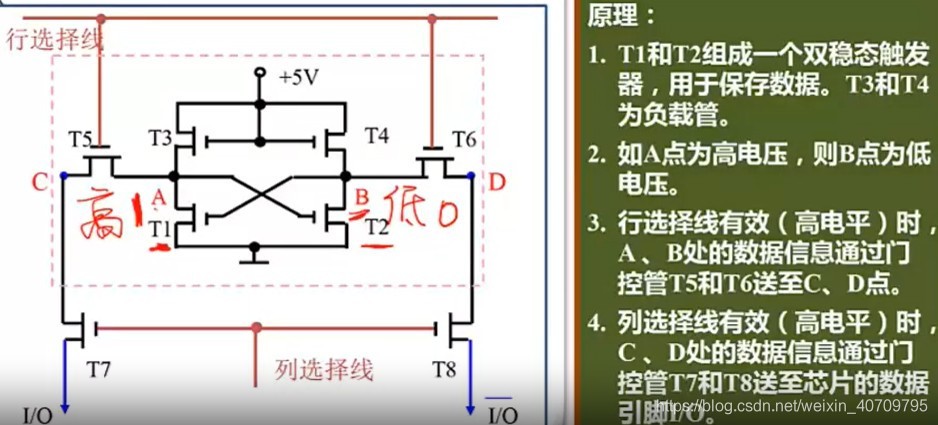
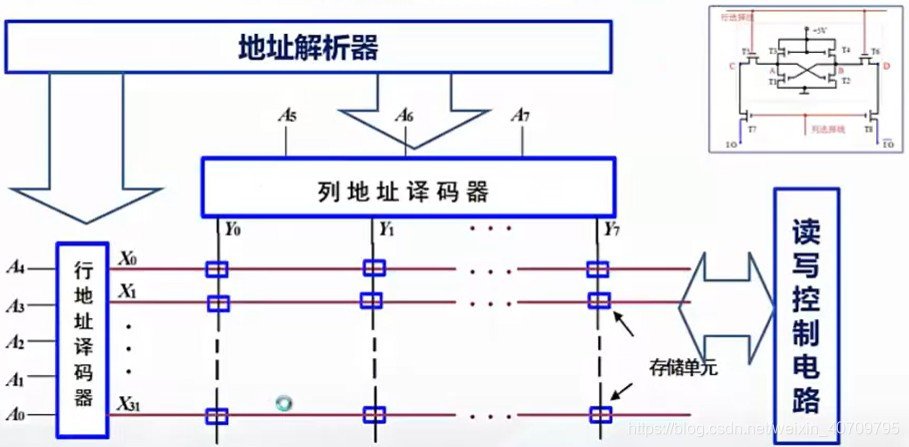
存储器的类型：

• RAM
  • DRAM(Dynamic RAM)(可随机存器，但必须周期性的刷新以保持存储内容，可用于制造内存)
  • SRAM(Static RAM)(可随机存取，不需要周期性刷新的存储器)
• ROM
  • ROM(掩膜ROM)
  • PROM(熔丝PROM)
  • EPROM(紫外线EPROM)
  • EEPROM(电可擦除ROM)
  • Flash EPROM(快速可编程只读存储器)

地址与数据单元：引入（为什么32G的CPU最大只能管理4G内存？）

2^32 = 4G

CPU指令的执行

CPU可以执行哪些指令？

CPU只能执行指令集中的指令。指令：表现为二进制码，长度随CPU类型而不同，包含1个或多个字节，分为指令码和操作数

程序的执行

源程序->编译->汇编->机器码