基于MATLAB计算相对论条件下碳14原子的半衰期

我们知道，在同一参考系下，观测者测得碳原子的半衰期为5730年。

如果物体运动的速率远小于光速，则适用经典物理学，否则就必须使用相对论条件，相对论条件下，洛伦兹变换系数公式为，其中c为光速，u为物体的运动速度。

本次使用MATLAB运行计算过程不需要生成曲线图形，但需要生成表格，而生成的表格只需要看右侧的工作区就可以了。

相对论一直是大学物理的重难点，我们需要弄明白一些事情：

第一，在同一参考系下，原子核的结构是不会改变的，也就是说，通常情况下放射性元素的半衰期是不受影响的，那么我们在同意惯性系下测得的碳14半衰期就都是5730年。

第二，物体运动速度越快，它所在的参考系时间流速就会越慢，不知道大家有没有看过《熊出没：重返地球》，六耳猫人阿布（莱尔特族）交代过，200万年前他来自地球，但由于自然环境的事故被迫在太空中漂泊blablabla之类……

废话少说！是这样的：阿布交代他在太空中漂泊了几年（设年数小于10），但是受黑洞周围时间流速的影响，地球已经过去几百万年了！（设地球过去的年数大于10的6次方）

这踏马差了好几个数量级！不会吧？差距这么大？

但这是真的，真真实实的。

因为：距离黑洞越远，时间的流速越快，距离黑洞越近，时间的流速越慢，黑洞处时间不流动，是静止的。

好了，那么正确的运算结果是：

如果地球上的时间流速更快，那么外星人看到地球上碳14经历完一个半衰期，他们星球经过的时间小于5730年；

如果地外行星上的时间流速更快，那么外星人看到地球上碳14经历完一个半衰期，他们星球经过的时间大于5730年；

我们打开MATLAB，编写程序，其中我们要让物体运动的相对论速度u能够根据程序手动代入，搭建程序完成后要编译无误才能运行。

参考代码如下：

clear;
%在同一惯性系下，观测者观察到碳14原子的衰变时间是5730年
prompt='请输入物体速度';
u=input(prompt);
A=sqrt(1-(u*3e8)^2/(3e8)^2);
Gama=1/A;
Time=5730;
%地球上时间的流速更快
%我们比地外行星先经历完一个碳14的半衰期
%地外行星观测者观察到地球上碳14原子衰变的时间小于5730年
Time1=5730/Gama;
%地外行星上时间的流速更快
%我们比地外行星后经历完一个碳14的半衰期
%地外行星观测者观察到地球上碳14原子衰变的时间大于5730年
Time2=5730*Gama;

编译无误后，命令行窗口处出现prompt对应的提示语句：

代入u=0.8（也就是光速的80%），按下Enter键，在工作区就能够看到相应的计算结果了：

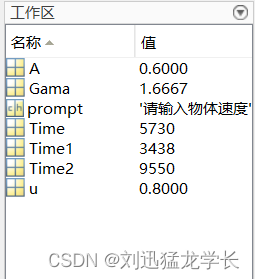
计算结果显示：当我们和某地外行星的相对运动速度为光速的80%时，如果地球时间流速更快，那么外星人目测过了3438年，我们经历完一个碳14的半衰期，如果地外行星时间流速更快，那么外星人目测过了9550年，我们才经历完一个碳14的半衰期。