
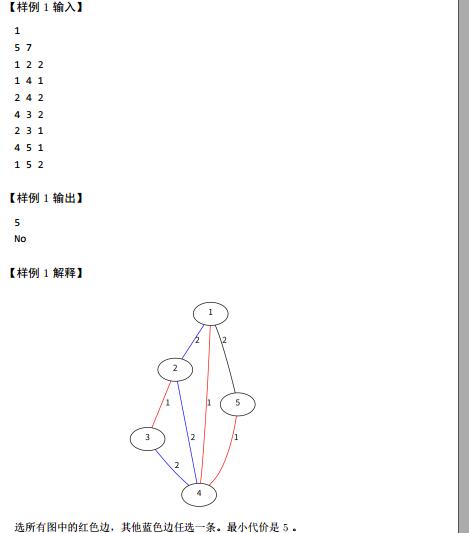
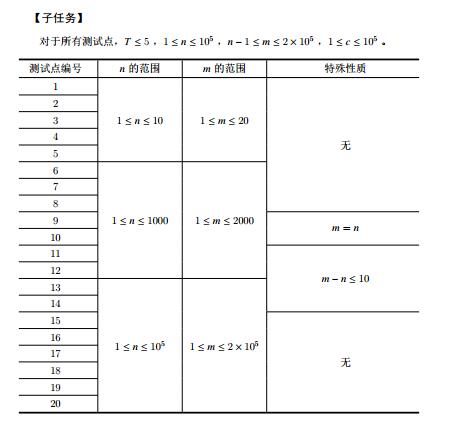
分析:第一问还是很好做的,关键是怎么做第二问.我们可以每次删掉最小生成树上的一条边,然后再求一次最小生成树,看边权和大小和原来的是不是一样的,不过这个做法效率很低.
考虑Kruskal算法的原理,每次加边权最小的边,如果边上的两个点不连通.如果在最小生成树的基础上把不是上面的边给加上去,就会形成环,在环上找除了这条边之外的最大边权,如果等于新加入的这条边,那么就有多个最小生成树.为什么这样呢?我们把最大边拿掉,添加进这条边,两个点还是连通的,边权和一定,只是在Kruskal的时候先考虑了那条最大边而已.
接下来只需要求出若干对点路径上的最大边权就可以了,我们可以用倍增算法来求.
写这道题的时候把w数组写成了e[i].w,挂惨了......以后要对同名数组多留意.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm>using namespace std;const int maxn = 400010;int T, n, m, head[maxn], nextt[maxn], to[maxn], w[maxn], tot = 1,fa[maxn],d[maxn],f[maxn][20],dmax[maxn][20]; long long ans; bool flag = false;struct node {int u, v, w,use; }e[maxn];void add(int x, int y, int z) {w[tot] = z;to[tot] = y;nextt[tot] = head[x];head[x] = tot++; }bool cmp(node a, node b) {return a.w < b.w; }int find(int x) {if (x == fa[x])return x;return fa[x] = find(fa[x]); }void dfs(int u, int depth,int from) {d[u] = depth;f[u][0] = from;for (int i = head[u]; i; i = nextt[i]){int v = to[i];if (v != from){dmax[v][0] = w[i];dfs(v, depth + 1, u);}} }int LCA(int x, int y) {if (x == y)return 0;if (d[x] < d[y])swap(x, y);int maxx = 0;for (int i = 19; i >= 0; i--)if (d[f[x][i]] >= d[y]){maxx = max(maxx, dmax[x][i]); x = f[x][i];}if (x == y)return maxx;for (int i = 19; i >= 0; i--)if (f[x][i] != f[y][i]){maxx = max(maxx, max(dmax[x][i], dmax[y][i]));x = f[x][i];y = f[y][i];}maxx = max(maxx, max(dmax[x][0], dmax[y][0]));return maxx; }int main() {scanf("%d", &T);while (T--){memset(head, 0, sizeof(head));tot = 1;ans = 0;flag = false;scanf("%d%d", &n, &m);memset(d, 0, sizeof(d));memset(f, 0, sizeof(f));memset(dmax, 0, sizeof(dmax));for (int i = 1; i <= n; i++)fa[i] = i;for (int i = 1; i <= m; i++){int a, b, c;scanf("%d%d%d", &a, &b, &c);e[i].u = a;e[i].v = b;e[i].w = c;e[i].use = 0;}sort(e + 1, e + 1 + m, cmp);for (int i = 1; i <= m; i++){int fx = find(e[i].u), fy = find(e[i].v);if (fx != fy){add(e[i].u, e[i].v, e[i].w);add(e[i].v, e[i].u, e[i].w);fa[fx] = fy;ans += e[i].w;e[i].use = 1;}}printf("%lld\n", ans);dfs(1, 1,0);for (int j = 1; j <= 19; j++)for (int i = 1; i <= n; i++){f[i][j] = f[f[i][j - 1]][j - 1];dmax[i][j] = max(dmax[i][j - 1], dmax[f[i][j - 1]][j - 1]);}for (int i = 1; i <= m; i++)if (!e[i].use && LCA(e[i].u, e[i].v) == e[i].w){flag = 1;break;}if (flag)puts("No");elseputs("Yes");}return 0; }









