冒泡排序及冒泡排序的优化-＞鸡尾酒排序

2023-10-28 16:10
文章标签 优化 排序 冒泡排序 鸡尾酒

本文主要是介绍冒泡排序及冒泡排序的优化-＞鸡尾酒排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

什么是冒泡排序

冒泡排序的英文Bubble Sort，是一种最基础的交换排序。
大家一定都喝过汽水，汽水中常常有许多小小的气泡，哗啦哗啦飘到上面来。这是因为组成小气泡的二氧化碳比水要轻，所以小气泡可以一点一点向上浮动。
冒泡排序（Bubble Sorting）的基本思想是：通过对待排序序列从前向后（从下标较小的元素开始）,依次比较 相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就象水底下的气泡一样逐渐向上冒。

演示冒泡过程的例子(图解)

在这里插入图片描述

小结上面的图解过程:
(1) 一共进行 数组的大小-1 次大的循环
(2)每一趟排序的次数在逐渐的减少
(3) 如果我们发现在某趟排序中，没有发生一次交换， 可以提前结束冒泡排序。这个就是优化

冒泡排序第一版

#include <iostream>
#include <string>
using namespace std;
/*数组遍历*/
void ListShow(int list[], int length){for (int i = 0; i < length; i++){cout << list[i] << "  ";}cout << endl;
}
/*==================冒泡排序==========================*/
void BubbleSort(int *list, int length)
{int temp; //定义中间变量cout << "====冒泡排序=====" << endl;for (int i = 0; i < length - 1; i++){ //数组长度为n，冒泡排序比较n-1趟//每趟中，数据两两比较，大的往后移for (int j = 0; j < length - i - 1; j++){if (list[j] > list[j + 1]){ //交换,从小往大,若>从大往小temp = list[j];list[j] = list[j + 1];list[j + 1] = temp;}}cout << "第" << i + 1 << "趟: ";ListShow(list, length);}
}
int main()
{int list[9] = {9, 3, 1, 4, 2, 7, 8, 6, 5};int length = sizeof(list) / sizeof(list[0]); //求数组的长度，C++固定方式cout << "排序前" << endl;ListShow(list, length);BubbleSort(list, length);cout << "排序后" << endl;ListShow(list, length);return 0;
}

冒泡排序第二版

这一版代码做了小小的改动，利用布尔变量flag作为标记。如果在本轮排序中，元素有交换，则说明数列无序；如果没有元素交换，说明数列已然有序，直接跳出大循环。

#include <iostream> //冒泡优化第二版，解决整体有序还在排问题
#include <string>
using namespace std;
void listshow(int list[], int length)
{for (int i = 0; i < length; i++){cout << list[i] << "  ";}cout << endl;
}
void bubblesort(int array[], int length)
{int temp;for (int i = 0; i < length - 1; i++){bool flage = true;for (int j = 0; j < length - i - 1; j++){if (array[j] > array[j + 1]){temp = array[j];array[j] = array[j + 1];array[j + 1] = temp;flage = false;}}if (flage){break;}else{cout << "第" << i + 1 << "次" << endl;listshow(array, length);}}
}int main()
{int a[7] = {3, 4, 1, 5, 6, 7, 8};int b = sizeof(a) / sizeof(a[0]);cout << "排序前" << endl;listshow(a, b);bubblesort(a, b);cout << "排序后" << endl;listshow(a, b);
}

冒泡排序第三版

为了说明这个问题，我们重新选择一个新的数列：
3 4 2 1 5 6 7 8
这个数列的特点是前半部分（3，4，2，1）无序，后半部分（5，6，7，8）升序，并且后半部分
的元素已经是数列最大值。
让我们按照冒泡排序的思路来进行排序，看一看具体效果：
第一轮
元素3和4比较，发现3小于4，所以位置不变。
元素4和2比较，发现4大于2，所以4和2交换。
元素4和1比较，发现4大于1，所以4和1交换。
元素4和5比较，发现4小于5，所以位置不变。
元素5和6比较，发现5小于6，所以位置不变。
元素6和7比较，发现6小于7，所以位置不变。
元素6和7比较，发现6小于7，所以位置不变。
第一轮结束，数列有序区包含一个元素：3 2 1 4 5 6 7 8
第二轮
元素3和2比较，发现3大于2，所以3和2交换。
元素3和4比较，发现3小于4，所以位置不变。
元素4和5比较，发现4小于5，所以位置不变。
元素5和6比较，发现5小于6，所以位置不变。
元素6和7比较，发现6小于7，所以位置不变。
元素7和8比较，发现7小于8，所以位置不变。
第二轮结束，数列有序区包含一个元素：2 1 3 4 5 6 7 8

这个问题的关键点在哪里呢？关键在于对数列有序区的界定。
按照现有的逻辑，有序区的长度和排序的轮数是相等的。比如第一轮排序过后的有序区长度是1，第二轮排序过后的有序区长度是2 …
实际上，数列真正的有序区可能会大于这个长度，比如例子中仅仅第二轮，后面5个元素实际都已经属于有序区。因此后面的许多次元素比较是没有意义的。
如何避免这种情况呢？我们可以在每一轮排序的最后，记录下最后一次元素交换的位置，那个位置也就是无序数列的边界，再往后就是有序区了。

#include <iostream> //冒泡优化第三版,后面部分已经有序
#include <string>
using namespace std;
void ListShow(int list[], int length)
{for (int i = 0; i < length; i++){cout << list[i] << "  ";}cout << endl;
}
void BubbleSort(int array[], int length)
{int t;int lastchange = 0; //记录最后一次交换的位置for (int i = 0; i < length - 1; i++){bool flage = true;				//有序标记，每一轮的初始是trueint sortbuder = length - i - 1; //无序数列的边界，每次比较只需要比到这里为止for (int j = 0; j < sortbuder; j++){if (array[j] > array[j + 1]){t = array[j];array[j] = array[j + 1];array[j + 1] = t;flage = false;		//有元素交换，所以不是有序，标记变为falselastchange = j + 1; //把无序数列的边界更新为最后一次交换元素的位置}}if (flage){break;}else{cout << "第" << i + 1 << "次" << endl;sortbuder = lastchange;ListShow(array, length);}}
}
int main()
{int a[] = {1, 44, 4, 5, 64, 34, 35, 36, 39};int b = sizeof(a) / sizeof(a[0]);cout<<"排序前"<<endl;ListShow(a, b);BubbleSort(a, b);cout<<"排序后"<<endl;ListShow(a, b);
}

这一版代码中，sortBorder就是无序数列的边界。每一轮排序过程中，sortBorder之后的元素就完全不需要比较了，肯定是有序的。

冒泡排序第四版（鸡尾酒排序）

鸡尾酒排序的元素比较和交换过程是双向的。
让我们来举一个栗子：
在这里插入图片描述
有8个数组成一个无序数列：2，3，4，5，6，7，8，1，希望从小到大排序
如果按照冒泡排序的思想，排序的过程是什么样呢？
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

可以看到从2到8已经是有序的了，只有1元素的位置不对，缺还要进行7轮排序，这也太憋屈了吧？
鸡尾酒排序正是解决这种问题

鸡尾酒的详细过程

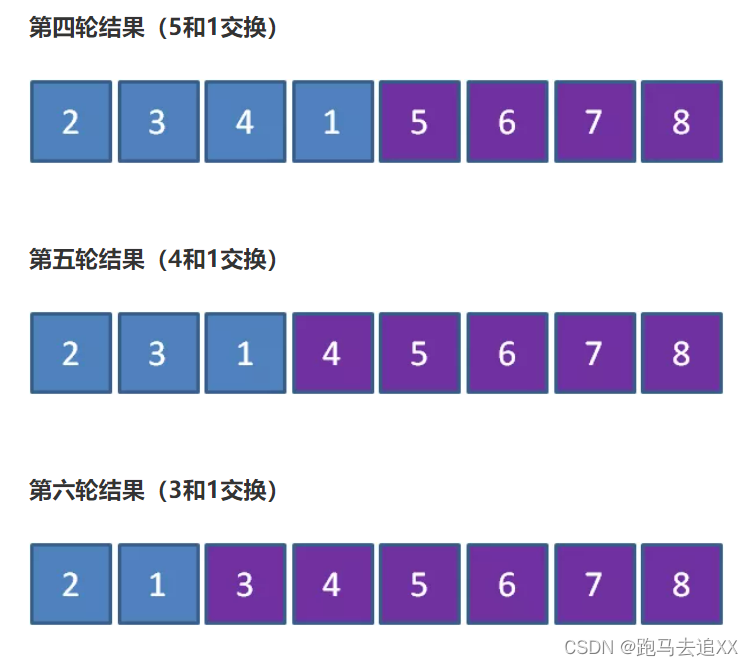
第一轮（和冒泡排序一样，8和1交换）
在这里插入图片描述
第二轮
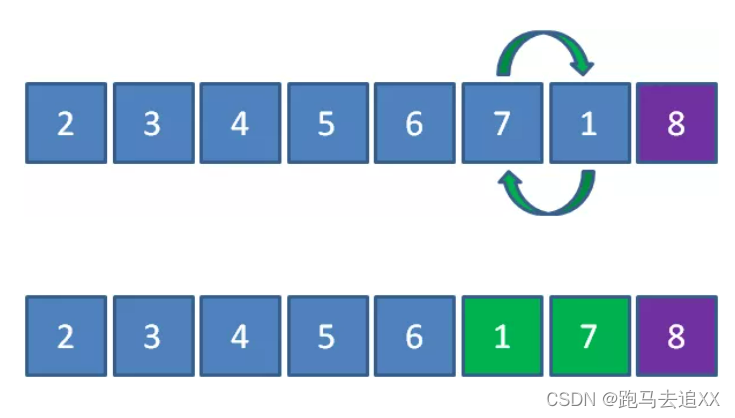
此时开始不一样了，我们反过来从右往左比较和交换：
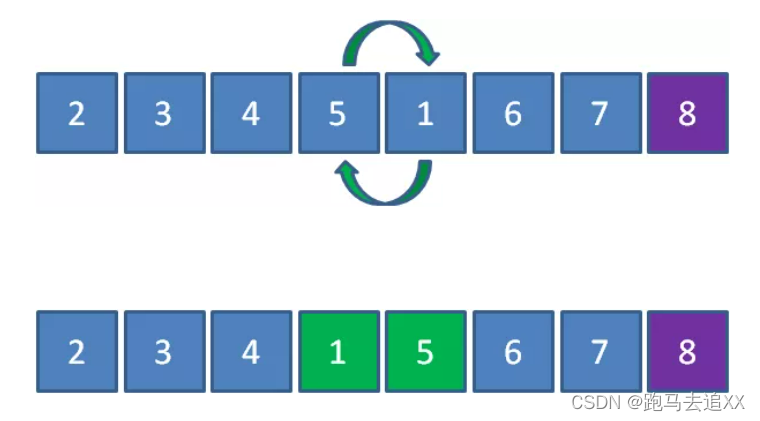
8已经处于有序区，我们忽略掉8，让1和7比较。元素1小于7，所以1和7交换位置：
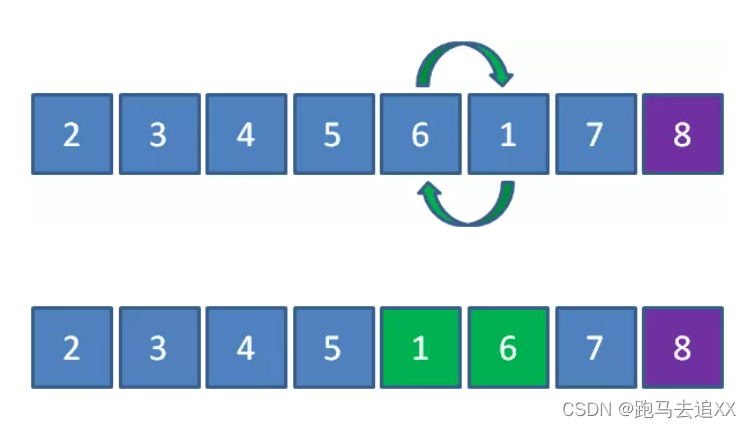
在这里插入图片描述
接下来1和6比较，元素1小于6，所以1和6交换位置
在这里插入图片描述
接下来1和5比较，元素1小于5，所以1和5交换位置：
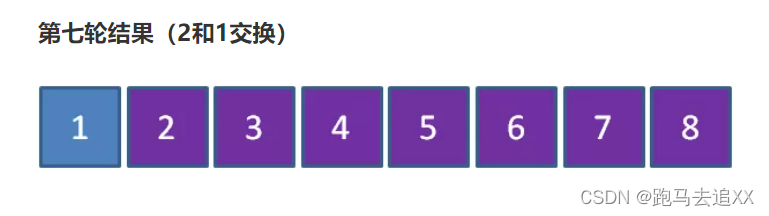
在这里插入图片描述
接下来1和4交换，1和3交换，1和2交换，最终成为了下面的结果：
在这里插入图片描述
第三轮（虽然已经有序，但是流程并没有结束）
鸡尾酒排序的第三轮，需要重新从左向右比较和交换：
1和2比较，位置不变；2和3比较，位置不变；3和4比较，位置不变…6和7比较，位置不变。
没有元素位置交换，证明已经有序，排序结束。

这就是鸡尾酒排序的思路。排序过程就像钟摆一样，第一轮从左到右，第二轮从右到左，第三轮再从左到右…

#include <iostream> //鸡尾酒排序,先从左向右，后从右向左
#include <string>
using namespace std;
void ListShow(int list[], int length)
{for (int i = 0; i < length; i++){cout << list[i] << "  ";}cout << endl;
}
void BubbleSort(int array[], int length)
{int t;for (int i = 0; i < length / 2; i++) //因为左右排序所以只需进行一半排序就可以了{cout << "第" << i + 1 << "趟" << endl;//奇数轮，从左向右比较和交换bool flage = true;for (int j = 0; j < length - i - 1; j++){if (array[j] > array[j + 1]){t = array[j];array[j] = array[j + 1];array[j + 1] = t;flage = false;}}if (flage){break;}else{cout << "从左到右第" << i + 1 << "次" << endl;ListShow(array, length);}//偶数轮之前，重新标记为trueflage = true;//偶数轮，从右向左比较和交换for (int j = length - i - 1; j > i; j--){if (array[j] < array[j - 1]){t = array[j];array[j] = array[j - 1];array[j - 1] = t;flage = false;}}if (flage){break;}else{cout << "从右到左第" << i + 1 << "次" << endl;ListShow(array, length);}}
}
int main()
{int a[] = {2, 3, 4, 5, 6, 7, 1, 8};int b = sizeof(a) / sizeof(a[0]);cout << "排序前" << endl;ListShow(a, b);BubbleSort(a, b);cout << "排序后" << endl;ListShow(a, b);
}

这段代码是鸡尾酒排序的原始实现。代码外层的大循环控制着所有排序回合，大循环内包含两个小循环，第一个循环从左向右比较并交换元素，第二个循环从右向左比较并交换元素。

冒泡排序第五版

鸡尾酒排序的优化

对于单向的冒泡排序，我们需要设置一个边界值，对于双向的鸡尾酒排序，我们需要设置两个边界值。请看代码：

#include <iostream> //鸡尾酒排序优化,先从左向右，后从右向左,优化
using namespace std;
void ListShow(int list[], int length)
{for (int i = 0; i < length; i++){cout << list[i] << "  ";}cout << endl;
}
void BubbleSort(int array[], int length)
{int LastRightExchange = 0; //记录右侧最后一次交换的位置int LastLeftExchange = 0;  //记录左侧最后一次交换的位置int LeftSortBorder = 0;	   //无序数列的左边界，每次比较只需要比到这里为止int RightSortBorder;	   //无序数列的右边界，每次比较只需要比到这里为止int t;for (int i = 0; i < length / 2; i++) //因为左右排序所以只需进行一半排序就可以了{cout << "第" << i + 1 << "趟" << endl;bool flage = true; //有序标记，每一轮的初始是trueRightSortBorder = length - i - 1;//奇数轮，从左向右比较和交换for (int j = LeftSortBorder; j < RightSortBorder; j++){if (array[j] > array[j + 1]){t = array[j];array[j] = array[j + 1];array[j + 1] = t;flage = false;LastRightExchange = j + 1;}}RightSortBorder = LastRightExchange;if (flage){break;}else{cout << "从左到右第" << i + 1 << "次" << endl;ListShow(array, length);}//偶数轮之前，重新标记为trueflage = true;//偶数轮，从右向左比较和交换for (int j = RightSortBorder; j > LeftSortBorder; j--){if (array[j] < array[j - 1]){t = array[j];array[j] = array[j - 1];array[j - 1] = t;flage = false;LastLeftExchange = j - 1;}}LeftSortBorder = LastLeftExchange;if (flage){break;}else{cout << "从右到左第" << i + 1 << "次" << endl;ListShow(array, length);}}
}
int main()
{int a[] = {2, 3, 4, 5, 6, 7, 1, 8};int b = sizeof(a) / sizeof(a[0]);cout << "排序前" << endl;ListShow(a, b);BubbleSort(a, b);cout << "排序后" << endl;ListShow(a, b);
}

这篇关于冒泡排序及冒泡排序的优化-＞鸡尾酒排序的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/294371。

相关文章

Python如何使用__slots__实现节省内存和性能优化

Python如何使用__slots__实现节省内存和性能优化

《Python如何使用__slots__实现节省内存和性能优化》你有想过,一个小小的__slots__能让你的Python类内存消耗直接减半吗,没错,今天咱们要聊的就是这个让人眼前一亮的技巧,感兴趣的... 目录背景：内存吃得满满的类__slots__：你的内存管理小助手举个大概的例子：看看效果如何？1.
阅读更多...
一文详解SpringBoot响应压缩功能的配置与优化

一文详解SpringBoot响应压缩功能的配置与优化

《一文详解SpringBoot响应压缩功能的配置与优化》SpringBoot的响应压缩功能基于智能协商机制,需同时满足很多条件,本文主要为大家详细介绍了SpringBoot响应压缩功能的配置与优化,需... 目录一、核心工作机制1.1 自动协商触发条件1.2 压缩处理流程二、配置方案详解2.1 基础YAML
阅读更多...
MySQL中慢SQL优化的不同方式介绍

MySQL中慢SQL优化的不同方式介绍

《MySQL中慢SQL优化的不同方式介绍》慢SQL的优化,主要从两个方面考虑,SQL语句本身的优化,以及数据库设计的优化,下面小编就来给大家介绍一下有哪些方式可以优化慢SQL吧... 目录避免不必要的列分页优化索引优化JOIN 的优化排序优化UNION 优化慢 SQL 的优化，主要从两个方面考虑，SQL 语
阅读更多...
MySQL中慢SQL优化方法的完整指南

MySQL中慢SQL优化方法的完整指南

《MySQL中慢SQL优化方法的完整指南》当数据库响应时间超过500ms时,系统将面临三大灾难链式反应,所以本文将为大家介绍一下MySQL中慢SQL优化的常用方法,有需要的小伙伴可以了解下... 目录一、慢SQL的致命影响二、精准定位问题SQL1. 启用慢查询日志2. 诊断黄金三件套三、六大核心优化方案方案
阅读更多...
Redis中高并发读写性能的深度解析与优化

Redis中高并发读写性能的深度解析与优化

《Redis中高并发读写性能的深度解析与优化》Redis作为一款高性能的内存数据库,广泛应用于缓存、消息队列、实时统计等场景,本文将深入探讨Redis的读写并发能力,感兴趣的小伙伴可以了解下... 目录引言一、Redis 并发能力概述1.1 Redis 的读写性能1.2 影响 Redis 并发能力的因素二、
阅读更多...
C++快速排序超详细讲解

C++快速排序超详细讲解

《C++快速排序超详细讲解》快速排序是一种高效的排序算法,通过分治法将数组划分为两部分,递归排序,直到整个数组有序,通过代码解析和示例,详细解释了快速排序的工作原理和实现过程,需要的朋友可以参考下... 目录一、快速排序原理二、快速排序标准代码三、代码解析四、使用while循环的快速排序1.代码代码1.由快
阅读更多...
使用国内镜像源优化pip install下载的方法步骤

使用国内镜像源优化pip install下载的方法步骤

《使用国内镜像源优化pipinstall下载的方法步骤》在Python开发中,pip是一个不可或缺的工具,用于安装和管理Python包,然而,由于默认的PyPI服务器位于国外,国内用户在安装依赖时可... 目录引言1. 为什么需要国内镜像源？2. 常用的国内镜像源3. 临时使用国内镜像源4. 永久配置国内镜
阅读更多...
C#原型模式之如何通过克隆对象来优化创建过程

C#原型模式之如何通过克隆对象来优化创建过程

《C#原型模式之如何通过克隆对象来优化创建过程》原型模式是一种创建型设计模式,通过克隆现有对象来创建新对象,避免重复的创建成本和复杂的初始化过程,它适用于对象创建过程复杂、需要大量相似对象或避免重复初... 目录什么是原型模式？原型模式的工作原理C#中如何实现原型模式？1. 定义原型接口2. 实现原型接口3
阅读更多...
Java嵌套for循环优化方案分享

Java嵌套for循环优化方案分享

《Java嵌套for循环优化方案分享》介绍了Java中嵌套for循环的优化方法,包括减少循环次数、合并循环、使用更高效的数据结构、并行处理、预处理和缓存、算法优化、尽量减少对象创建以及本地变量优化,通... 目录Java 嵌套 for 循环优化方案1. 减少循环次数2. 合并循环3. 使用更高效的数据结构4
阅读更多...
Spring排序机制之接口与注解的使用方法

Spring排序机制之接口与注解的使用方法

《Spring排序机制之接口与注解的使用方法》本文介绍了Spring中多种排序机制,包括Ordered接口、PriorityOrdered接口、@Order注解和@Priority注解,提供了详细示例... 目录一、Spring 排序的需求场景二、Spring 中的排序机制1、Ordered 接口2、Pri
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2