本文主要是介绍数值分析作业：圆周上n个点连成的线将圆分割成多少区域，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
参考视频：【官方中配】分圆问题，诡异的数列规律：解答篇_哔哩哔哩_bilibili
已知圆上任取n点，使得连接所有点得到的弦把圆盘分割成最多的片数是n的某个多项式（次数不炒股5次）
首先，为了使得直线将圆盘分割成最多片数，任意三条直线不能相交于同一点。
由组合公式可知，圆上取n个点，那能够形成的直线条数就是：
接下来寻找这些直线构成的交点数量，如果直接从直线相交角度考虑，那么很难寻找到全部的交点数量（有的直线会在圆外形成交点，这不在我们的考虑范围内），因此从另外一个角度考虑：圆上的任意四个点能够形成一个交点
那么，这些直线在圆内构成的交点数量就是：
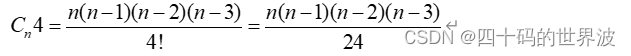
根据欧拉示性数公式（Euler’s Characteristic Formula）：
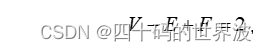
因此要求的最终分割片数就是：
由于是圆上的点以及直线相交的点共同分割区域，因此实际上点的数量：
条直线被 个点分割成的直线数加上圆周上的分割的圆的数量就是边的数量：
忽略圆外的区域，需要在原来基础上减一去除圆外区域，所以最终得到的区域数：
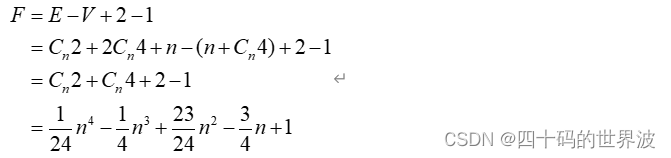
这就是最终得到的分割块数，是一个四次多项式。
要求给定13个点时，能够分割的最大块数只需要带入13
求得分割的区域数为794
这篇关于数值分析作业：圆周上n个点连成的线将圆分割成多少区域的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
