本文主要是介绍Expressing Arbitrary Reward Functions as Potential-Based Advice将任意奖励函数表示为基于势能的建议,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要
------有效地吸纳外部建议是强化学习中的一个重要问题,尤其是在它进入现实世界的时候。基于势能的奖励塑形是在保证策略不变性的前提下,为agent提供特定形式的额外奖励的一种方式。本文提出了一种新的方法,通过隐含地将任意一个具有相同保证的奖励函数转化为动态建议势能的特定形式,使其保持为一个同时学习的辅助值函数。我们证明了这种方式提供的建议捕获了期望中的输入奖励函数,并通过实证证明了其有效性。
1. Introduction
------实验心理学中的“塑形”一词(至少可以追溯到(Skinner 1938))指的是奖励所有导致期望行为的行为,而不是等待agent自发地表现出来(对于复杂的任务,这可能需要过长的时间)。例如,斯金纳发现,为了训练一只老鼠推动杠杆,任何朝杠杆方向移动的动作都必须得到奖励。强化学习(RL)是一个框架,agent从与环境的交互中学习,通常以白板式的方式,保证最终学习所需的行为。与斯金纳的老鼠一样,RL agent可能需要很长时间才能偶然发现目标杠杆,如果它得到的唯一强化(或奖励)是在这个事实之后,并通过提供额外的奖励来加快学习过程。
------RL 中的塑形从很早就与奖励函数有关; Mataric (1994)将塑形解释为设计一个更复杂的奖励函数,Drigo 和 Colombetti (1997)在一个真实的机器人上使用塑形来将专家指令转化为agent执行任务时的奖励,Randløv 和 Alstrøm (1998)提出学习 RL 信号的层次结构,试图将额外的强化函数从基本任务中分离出来。正是在同一篇论文中,他们揭示了以一种不受约束的方式修改奖励信号的问题:当教一名agent骑自行车,并鼓励他们朝着目标前进时,agent会“分心”,相反,他会学会骑车循环,永远获得积极的奖励。Ng,Harada和Russell(1999)解决了正向奖励循环的问题,他们设计了基于势能的奖励塑形(PBRS)框架,该框架将塑形奖励约束为过渡状态的势能函数差的形式。事实上,他们证明了一个更有力的主张,即这种形式对于保持原始任务不变是必要的。这一优雅且可实施的框架引发了奖励塑形研究的爆炸式发展,并被证明非常有效(Asmuth、Littman和Zinkov 2008)、(Devlin、Kudenko和Grzes 2011)、(Brys等人2014)、(Snel和Whiteson 2014)。Wiewiora、Cottorell和Elkan(2003)将PBRS扩展到陈述行动建议势能,Devlin和Kudenko(2012)最近将PBRS推广到处理动态势能,允许agent学习时在线改变势能函数。
------早期 RS 研究的附加奖励函数虽然对策略保留有危险,但能够直接传递行为知识(例如专家指令)。势能函数需要额外的抽象,限制了额外有效奖励的形式,但提供了至关重要的理论保证。我们试图在可获得的行为知识和有效的基于势能的奖励之间架起一座桥梁。本文给出了一种新的方法,直接通过任意的奖励函数来指定有效的塑形奖励,同时隐式地保持策略不变性所必需的势能基础。为此,我们首先将Wiewiora的建议框架扩展到动态建议势能。然后,我们建议并行学习一个二阶价值函数,它是我们任意奖励函数的一个变体,并使用其连续估计作为我们的dynamic advice potentials。我们表明,有效的塑形奖励然后反映了期望中的输入奖励函数。(研究表明,有效的塑形奖励反映了期望中的输入奖励函数。)。经验上,我们首先演示了我们的方法,以避免在网格世界任务中出现正向奖励循环的问题,同时给出了与骑自行车者相同的行为知识(Randløv和Alstrøm 1998)。然后,我们展示了一个应用程序,其中我们的动态(PB)价值函数建议优于编码相同知识的其他奖励塑造方法,以及一种不同的流行启发式的塑形方法。
2. Background
------我们假设通常的强化学习框架(Sutton和Barto 1998),在该框架中,agent以离散时间步长 t = 1 , 2 , … … t=1,2,…… t=1,2,……与马尔可夫环境交互。形式上,马尔可夫决策过程(MDP)(Puterman 1994)是一个元组 M = < S , A , γ , T , R > M=<S,A,γ,T,R> M=<S,A,γ,T,R>,其中:S是一组状态,A是一组动作, γ ∈ [ 0 , 1 ] γ∈[0,1] γ∈[0,1]是贴现因子, T = P s a ( ⋅ ) ∣ s ∈ S , a ∈ A T={Psa (·)|s∈S,a∈A} T=Psa(⋅)∣s∈S,a∈A是下一个状态转移概率, P s a ( s ′ ) P_{sa}(s') Psa(s′)指定从状态s采取动作a时发生状态s’的概率, R : S × A → R R: S×A→ \mathbb{R} R:S×A→R是期望的奖励函数,其中 R ( s , a ) R(s,a) R(s,a)给出了在状态s中获取a时将接收的奖励的期望(相对于T)值。
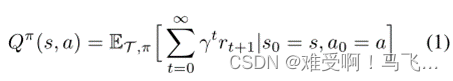
------从现在起,我们将省略 E E E上的下标,并暗示所有关于 T T T, π π π的期望。通过在每个状态下选取最大值的动作,可以获得(确定性)贪婪策略:
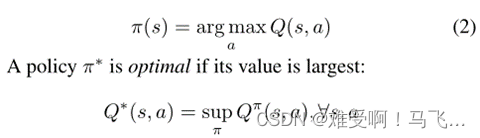
当 Q Q Q 值对给定的策略 π π π 是精确的时候,它们满足以下递归关系(Bellman 1957) :

通过以下更新可以逐步了解这些值:
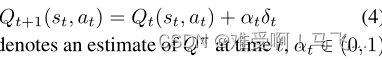
其中 Q t Q_t Qt 表示时间 t t t 的 Q π Q_π Qπ 估计, α t ∈ ( 0 , 1 ) α_t∈(0,1) αt∈(0,1)是时间 t t t 的学习速率,并且
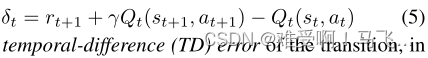
是转换的时间差(TD)误差,其中 a t a_t at和 a t + 1 a_{t+1} at+1都是根据 π π π选择的。在标准近似条件下(Jaakkola、Jordan和Singh 1994),该过程收敛于极限的正确值估计(TD不动点)。
3. Reward Shaping
RL 中最一般的奖励形式可以给出为修改势能 MDP 的奖励函数:
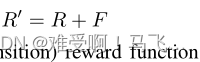
------其中 R R R是基本问题的奖励函数, F F F是塑形奖励函数,其中 F ( s , a , s ′ ) F(s,a,s') F(s,a,s′)在过渡 ( s , a , s ′ ) (s,a,s') (s,a,s′)上给出附加奖励得到新的过度 ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′),并且 f t f_t ft的定义与 r t r_t rt类似。我们将始终将框架称为奖励塑形,将辅助奖励(auxiliary reward)本身称为塑形奖励。
------PBRS (Ng,Harada,and Russell 1999)保持了一个势能函数 Φ : S → R Φ: S→\mathbb{R} Φ:S→R,并将塑形奖励函数 F F F 约束为以下形式:
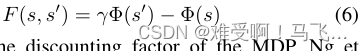
------其中 γ γ γ 是 MDP 的折现因子。Ng 等人(1999)证明了这种形式对于策略不变性是必要且充分的。
Wiewiora等人(2003)将PBRS扩展到建议在联合状态-动作空间上定义的势能函数。请注意,这个扩展添加了 F F F对所遵循的策略的依赖性(除了执行的转换)。作者考虑了两种类型的建议:向前看和向后看,为前者提供了理论框架:
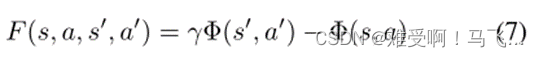
Devlin和Kudenko(2012)通过包括时间参数,将等式(6)中的形式推广到动态势能,并表明PBRS的所有理论性质都成立。
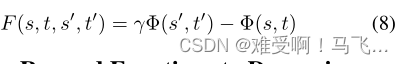
4. 从奖励函数到动态势能
------PBRS 存在两个(相互关联的)问题: 有效性和规范性。前者与设计最佳的势能函数有关,即那些提供最快和最流畅指导的函数。后者是指以最简单和最有效的方式将可用的领域知识捕获到一种势能的形式。这项工作主要处理后一个问题。
------以势能的形式锁定知识是一种方便的理论范式,但在考虑所有类型的领域知识时,可能会受到限制,尤其是行为知识,这些知识可能会以动作的形式具体化。例如,假设一位专家希望在一个状态s中鼓励一个动作 a a a。
------如果按照建议框架,它将 Φ ( s , a ) Φ(s,a) Φ(s,a)设置为1,而 Φ Φ Φ在其他位置的值为零,则与转换 ( s , a , s ′ ) (s,a,s') (s,a,s′)相关的塑形奖励将为 F ( s , a , s ′ , a ′ ) = Φ ( s ′ , a ′ ) − Φ ( s , a ) = 0 − 1 = − 1 F(s,a,s',a')=Φ(s',a')−Φ(s,a)=0−1=−1 F(s,a,s′,a′)=Φ(s′,a′)−Φ(s,a)=0−1=−1,只要状态-动作对 ( s ′ , a ′ ) (s',a') (s′,a′)不同于 ( s , a ) (s,a) (s,a)。有利的行为(behavior) ( s , a ) (s,a) (s,a)将实际上被劝阻。它可以通过进一步指定从状态 s s s通过动作 a a a可到达的状态-动作 Φ Φ Φ来避免这种情况,但这需要了解MDP。因此,它想做的是能够直接指定期望的有效塑形奖励 F F F,但不牺牲基于势能的框架提供的最佳性。
------这项工作制定了一个框架来实现这一点。给定任意奖励函数 R † R^† R†,我们希望实现 F ≈ R † F≈R^† F≈R†(约等于),同时保持策略不变。这个问题相当于根据 R † R^† R†求一个势能函数 Φ Φ Φ,服从 F Φ ≈ R † F_Φ≈R^† FΦ≈R†,其中(以及未来),我们用 F Φ F_Φ FΦ表示相对于 Φ Φ Φ的基于势能的塑形奖励。
------我们方法的核心思想是引入一个二级(状态-动作)价值函数 Φ Φ Φ,它与主要过程同时学习专家提供的奖励 R † R^† R† 的负数 R Φ R^Φ RΦ,并使用 Φ t Φ_t Φt 的连续更新值作为动态势能函数,从而使转化为隐式势能。正式地:
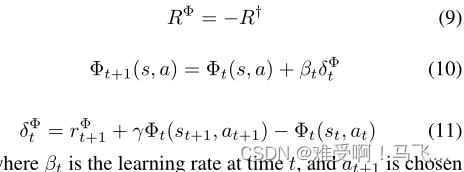
其中, β t β_t βt是时间t时的学习速率,根据策略 π π π相对于主要任务的值函数 Q Q Q选择 a t + 1 a_{t+1} at+1。塑形奖励的形式如下:
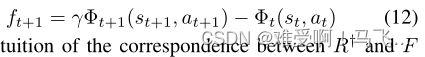
R † R^† R†和 F F F之间对应关系的直觉在于Bellman方程(对于 Φ Φ Φ)之间的关系:
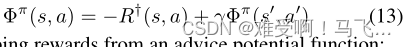
并通过建议势能函数来塑形奖励(shaping rewards):
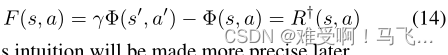
这种直觉将在以后更加精确。
5. Theory
------本节组织如下。首先,我们将基于势能的建议框架扩展到基于动态势能的建议,并确保所需的保证有效。(我们的动态(基于势能的)价值函数建议就是基于势能的动态建议的一个实例。)然后我们转向 R † R^† R†和 F F F之间的对应关系问题,表明F在预期中捕获了 R † R^† R†。最后,我们通过论证趋同来确保这些期望是有意义的。
5.1 基于动态势能的建议
------类似于(Devlin和Kudenko 2012),我们用一个时间参数来增强Wiewiora的前瞻性建议函数(等式(7)),以获得我们基于动态势能的建议: F ( s , a , t , s ′ , a ′ , t ′ ) = γ Φ ( s ′ , a ′ , t ′ ) − Φ ( s , a , t ) F(s,a,t,s',a',t')=γΦ(s',a',t')−Φ(s,a,t) F(s,a,t,s′,a′,t′)=γΦ(s′,a′,t′)−Φ(s,a,t),其中 t / t ′ t/t' t/t′是agent访问状态 s / s ′ s/s' s/s′并采取动作 a / a ′ a/a' a/a′的时间。为了表示简洁,我们将形式改写为:
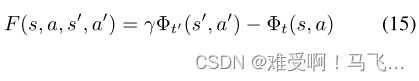
其中我们隐式地将 s s s与 s t s_t st关联,将 s ′ s' s′与 s t ′ s_{t'} st′关联,将 F ( s , a , s ′ , a ′ ) F(s,a,s',a') F(s,a,s′,a′)与 F ( s , a , t , s ′ , a ′ , t ′ ) F(s,a,t,s',a',t') F(s,a,t,s′,a′,t′)关联。与Wiewiora的框架一样, F F F现在不仅是转换 ( s , a , s ′ ) (s,a,s') (s,a,s′)的函数,而且是下面的动作 a ′ a' a′,这增加了对agent当前正在评估的策略的依赖性。
我们研究了原始 MDP 的最佳 Q 值的变化,这是由于在基本奖励函数 R 中加入 F 而导致的。

因此,一旦学习了 R + F R+F R+F最优策略,为了揭示 R + F R+F R+F的最优策略,可以使用有偏见的贪婪行为选择(Wiewiora,Cottrell,和Elkan 2003)来计算动态建议函数的初始值。
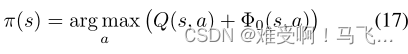
注意,当建议(advice)函数被初始化为0时,上面的有偏贪婪动作选择(action-selection)减少为基本贪婪策略(等式2),允许对简单的状态势能同样无缝地使用动态建议。
5.2 期望的塑形
设 R † R^† R†为任意奖励函数,设 Φ Φ Φ为在 R Φ = − R † R_Φ=−R^† RΦ=−R†,同时遵循一些固定策略 π π π。作为动态建议函数,在时间步长t相对于 Φ Φ Φ的塑形奖励由下式给出:

现在假设这个过程已经收敛到 TD 不动点 Φ π Φ_π Φπ,然后:

------因此,我们得出,相对于收敛值 Φ π Φ_π Φπ,塑形奖励F反映了预期设计者奖励 R † ( s , a ) R^†(s,a) R†(s,a)加上偏置项,该偏置项测量采样的下一状态-动作值与预期下一状态行动值的差。这种偏置项将在每次转变中进一步鼓励“比预期更好”(反之亦然)的转变,类似地,例如,在R-learning中,向“比平均更好”(反过来亦然)奖励的转变(Schwartz 1993)。
------为了获得预期的塑形奖励 F ( s , a ) F(s,a) F(s,a),我们将期望值与转移矩阵 t t t和选择 a ′ a' a′的策略 π π π相比较。
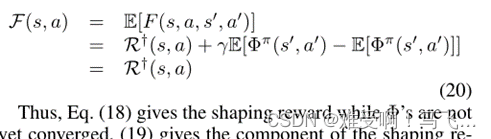
因此,等式(18)给出了 Φ Φ Φ尚未收敛时的塑形奖励,(19)给出了在 Φ π Φ_π Φπ正确后的转变上的成形奖励的分量,(20)建立了 F F F和 R † R^† R†的期望等价性。
5.3 Φ 的收敛性
------如果策略 π π π是固定的,并且 Q π Q_π Qπ-估计是正确的,那么上一节中的预期是明确的, Φ Φ Φ收敛于TD不动点。然而, Φ Φ Φ与 Q Q Q同时学习。通过在两个时间尺度上制定框架(Borkar 1997),并使用Borkar和Meyn(2000)的ODE方法,可以证明该过程收敛。因此,我们要求步长调度{ α t α_t αt}和{ β t β_t βt}满足以下条件:

------ Q Q Q和 Φ Φ Φ分别对应较慢和较快的时间尺度。考虑到步长调度差异,我们可以将迭代(对于 Q Q Q和 Φ Φ Φ)改写为一次迭代,使用组合参数向量,并表明Borkar和Meyn(2000)的假设(A1)-(A2)得到满足,这允许应用他们的定理2.2。该分析类似于带梯度校正的TD收敛((Sutton等人,2009)中的定理2),并且为了说明清楚而省略。
------请注意,需要这种收敛来确保 Φ Φ Φ确实捕获了专家奖励函数 R † R^† R†。来自等式(15)的一般动态建议的形式本身对 Φ Φ Φ的收敛性质没有任何要求,以保证策略不变性。
这篇关于Expressing Arbitrary Reward Functions as Potential-Based Advice将任意奖励函数表示为基于势能的建议的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





