Reids—HyperLogLog解决统计问题

HyperLogLog简介

HyperLogLog 是最早由 Philippe Flajolet及其同事在 2007 年提出的一种 估算基数的近似最优算法，Redis在 2.8.9 版本才添加了 HyperLogLog，HyperLogLog算法是用于基数统计的算法，每个 HyperLogLog 键只需要花费 12 KB 内存，就可以计算接近 2^64 个不同元素的基数。HyperLogLog适用于大数据量的统计，因为成本相对来说是更低的，最多也就占用12kb内存。

HyperLogLog只能统计基数的大小（也就是数据集的大小，集合的个数），他不能存储元素的本身，不能向set集合那样存储元素本身，也就是说无法返回元素。

HyperLogLog指令都是pf(PF)开头，这是因为HyperLogLog的发明人是Philippe Flajolet，pf是他的名字的首字母缩写。

基数统计(Cardinality Counting) 通常是用来统计一个集合中不重复的元素个数。

什么是基数?

比如数据集 {1, 3, 5, 7, 5, 7, 8}， 那么这个数据集的基数集为 {1, 3, 5 ,7, 8}, 基数(不重复元素)为5。 基数估计就是在误差可接受的范围内。

业务场景

HyperLogLog常用于大数据量的统计，比如页面访问量统计或者用户访问量统计，有两种不同的场景：

• UV（Unique Visitor）：独立访客，每个用户每天只记录一次
• PV（Page View）：浏览量，用户没点一次记录一次

如果统计PV，我们会想到使用Redis的incr、incrby指令，给每个网页配置一个独立Redis计数器就可以了，把这个计数器的 key 后缀加上当天的日期，这样一个请求过来，就执行incr incrby指令一次，最终就可以统计出所有的 PV 数据了。

但是UV和PV不同，UV需要根据用户的 ID 去重，同一个用户一天之内的多次访问请求只能计数一次。这就要求了每一个网页请求都需要带上用户的 ID，无论是登录用户还是未登录的用户，都需要一个唯一 ID 来标识
​
此时你可能会想到用如下方案解决这个问题：

• 存储在MySQL数据库表中，使用distinct count计算不重复的个数
• 使用Redis的set、hash、bitmaps等数据结构来存储，比如使用set，为每一个页面设置一个独立的 set 集合来存储所有当天访问过此页面的用户 ID

但是这么做会有以下两个比较大的问题：

• 随着数据量的增加，存储数据的空间占用越来越大，对于非常大的页面的UV统计，基本不符合实际操作
• 统计的性能比较慢，虽然可以通过异步方式统计，但是性能并不理想

Redis 中提供的 HyperLogLog 就是专门用来解决这个问题的，HyperLogLog 提供了一套不是很精确但是够用的去重方案，会有误差，官方给出的误差数据是 0.81%，这个精确度，对于UV这种统计来说这样的误差范围是被允许的。

因此针对UV的统计，我们将会考虑使用Redis的新数据类型HyperLogLog来实现。

HyperLogLog操作指令

pfadd key element [element …]：

将指定的元素添加到 HyperLogLog 中，每添加一个元素的复杂度为 O(1) 。如果 HyperLogLog 估计的近似基数在命令执行之后出现了变化， 那么命令返回 1 ， 否则返回 0 。 如果命令执行时给定的键不存在， 那么程序将先创建一个空的 HyperLogLog 结构， 然后再执行命令。

返回值：
如果HyperLogLog数据结构内部存储的数据被修改了，那么返回1，否则返回0

案例：

# 如果给定的键不存在，那么命令会创建一个空的 HyperLogLog，并向客户端返回 1
127.0.0.1:6379> pfadd name "pfadd1.0" "pfadd2.0"
(integer) 1
# 元素估计数量没有变化，返回 0（因为已经存在）
127.0.0.1:6379> pfadd name "pfadd1.0"
(integer) 0
# 添加一个不存在的元素，返回 1。注意，此时 HyperLogLog 内部存储会被更新，因为要记录新元素
127.0.0.1:6379> pfadd name "pfadd3.0"
(integer) 1

pfcount key [key …]

当 pfcount key [key …] 命令作用于单个键时，返回储存在给定键的 HyperLogLog 的近似基数，如果键不存在，那么返回 0，复杂度为 O(1)，并且具有非常低的平均常数时间；

当 pfcount key [key …] 命令作用于多个键时，返回所有给定 HyperLogLog 的并集的近似基数，这个近似基数是通过将所有给定 HyperLogLog 合并至一个临时 HyperLogLog 来计算得出的，复杂度为 O(N)，常数时间也比处理单个 HyperLogLog 时要大得多。

返回值：
返回给定HyperLogLog包含的唯一元素的近似数量的整数值

案例：

# 返回 name 包含的唯一元素的近似数量
127.0.0.1:6379> pfcount name
(integer) 3
127.0.0.1:6379> pfadd name "pfadd4.0"
(integer) 1
127.0.0.1:6379> pfcount ip_20190301
(integer) 4
127.0.0.1:6379> pfadd name2 "pfadd5.0" "pfadd6.0" "pfadd7.0"
(integer) 1
# 返回 name 和 name2 包含的唯一元素的近似数量
127.0.0.1:6379> pfcount name name2
(integer) 7

pfmerge destkey sourcekey [sourcekey …]

将多个 HyperLogLog 合并（merge）为一个 HyperLogLog，合并后的 HyperLogLog 的基数接近于所有输入 HyperLogLog 的可见集合（observed set）的并集。时间复杂度是 O(N)，其中 N 为被合并的 HyperLogLog 数量，不过这个命令的常数复杂度比较高。

命令格式：PFMERGE destkey sourcekey [sourcekey …]，合并得出的 HyperLogLog 会被储存在 destkey 键里面，如果该键并不存在，那么命令在执行之前，会先为该键创建一个空的 HyperLogLog。

返回值：
字符串回复，返回OK

案例

# mergeName 是 name  与 name2 并集
127.0.0.1:6379> pfmerge mergeName name name2
OK
127.0.0.1:6379> pfcount mergeName 
(integer) 7

HyperLoglog适用的场景

这里以日期统计1天、7天、一个月的数据为例。

我们上面说过如果把用户信息放到集合中（HashSet），如果数量不是很多还好，假如每天访问的用户有几百万，会占用大量的存储空间，且计算月活时，还需要将一个整月的数据放到一个 Set 中，这随时可能导致我们的程序 OOM。

而有了 HyperLogLog，就让事情变得简单了，因为存储日活数据所需要的内存只有 12K，例如：

1001_20211206
1002_20211207
1003_20211208
1004_20211209
...
1005_202112010

上面说过Redis使用incr 或者incrby执行，把计算器的可以后缀加上当天的日期,HyperLogLog也是可以这么使用的，比如：计算某一天的日活，只需要执行 pfcount 用户id_20211206XX 就可以了。每个月的第一天，执行 pfmerge 将上一个月的所有数据合并成一个 HyperLogLog，例如：用户id_20211206。再去执行 pfcount 用户id_20211206，就得到了 3 月的月活。

java中使用HyperLogLog

	private final RedisTemplate redisTemplate;public void hyperLogLog() throws ParseException {HyperLogLogOperations operations = redisTemplate.opsForHyperLogLog();// add 方法对应 pfadd 命令operations.add("user_20211206", "1001", "1002", "1003");// size 方法对应 pfcount 命令System.out.println(operations.size("user_20211206"));     // 3operations.add("user_20211206", "1001", "1004");System.out.println(operations.size("user_20211206"));     // 4operations.add("user_20211207", "1001", "1005");System.out.println(operations.size("user_20211207"));     // 2// union 方法对应 pfmerge 命令operations.union("user_20211208", "user_20211206", "user_20211207");System.out.println(operations.size("ip_201903"));       // 5}

HyperLogLog 原理

伯努利试验

HyperLogLog的算法设计只需要12k的内存就能统计2^64个数据（标准误差为0.81%），这个和伯努利试验有很大的关系，因此在探究HyperLogLog原理之前，需要先了解一下伯努利试验。

以下的图是百度百科的解释：

而它算法的最本源则是伯努利过程。伯努利过程就是一个抛硬币实验的过程。

硬币有正反两面，每次抛硬币出现正反面的概率都是50%。假设一直抛硬币，直到它出现正面为止，我们记录为一次完整的试验，可能抛了一次就出现了正面，也可能抛了4次才出现正面。无论抛了多少次，只要出现了正面，就记录为一次试验。这个试验就是伯努利试验。

那么对于多次的伯努利试验，假设这个多次为n次。就意味着出现了n次的正面。假设每次伯努利试验所经历了的抛掷次数为k。第一次伯努利试验，次数设为k1，以此类推，第n次对应的是kn。

其中，对于这n次伯努利试验中，必然会有一个最大的抛掷次数k，例如抛了12次才出现正面，那么称这个为k_max，代表抛了最多的次数。

伯努利试验容易得出有以下结论：

• n 次伯努利过程的投掷次数都不大于 k_max
• n 次伯努利过程，至少有一次投掷次数等于 k_max

最终结合极大似然估算的方法，发现在n和k_max中存在估算关联：n = 2^(k_max) 。这种通过局部信息预估整体数据流特性的方法似乎有些超出我们的基本认知，需要用概率和统计的方法才能推导和验证这种关联关系。

例如下面的样子：

• 第一次试验: 抛了3次才出现正面，此时 k=3，n=1
• 第二次试验: 抛了2次才出现正面，此时 k=2，n=2
• 第三次试验: 抛了6次才出现正面，此时 k=6，n=3
• 第n 次试验：抛了12次才出现正面，此时我们估算， n = 2^12

假设上面例子中实验组数共3组，那么 k_max = 6，最终 n=3，我们放进估算公式中去，明显： 3 ≠ 2^6 。也即是说，当试验次数很小的时候，这种估算方法的误差是很大的。

估值优化

在上面的3组例子中，我们称为一轮的估算。如果只是进行一轮的话，当 n 足够大的时候，估算的误差率会相对减少，但仍然不够小。

那么是否可以进行多轮呢？例如进行 100 轮或者更多轮次的试验，然后再取每轮的 k_max，再取平均数，即: k_mx/100。最终再估算出 n。下面是LogLog的估算公式：

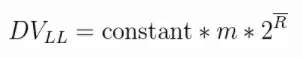
上面公式的DVLL对应的就是n，constant是修正因子，它的具体值是不定的，可以根据实际情况而分支设置。m代表的是试验的轮数。头上有一横的R就是平均数：(k_max_1 + … + k_max_m)/m。

这种通过增加试验轮次，再取k_max平均数的算法优化就是LogLog的做法。而 HyperLogLog和LogLog的区别就是，它采用的不是平均数，而是调和平均数。调和平均数比平均数的好处就是不容易受到大的数值的影响。下面举个例子：

求平均工资:
假如小明工资是1000/月，小红的工资是30000/月。

• 使用平均数的方式就是： (1000 + 30000) / 2 = 15500
• 使用调和平均数的方式就是： 2/(1/1000 + 1/30000) ≈ 1935.484

明显地，调和平均数比平均数的效果是要更好的。

下面是调和平均数的计算方式，∑ 是累加符号。

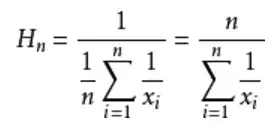
HyperLogLog的实现

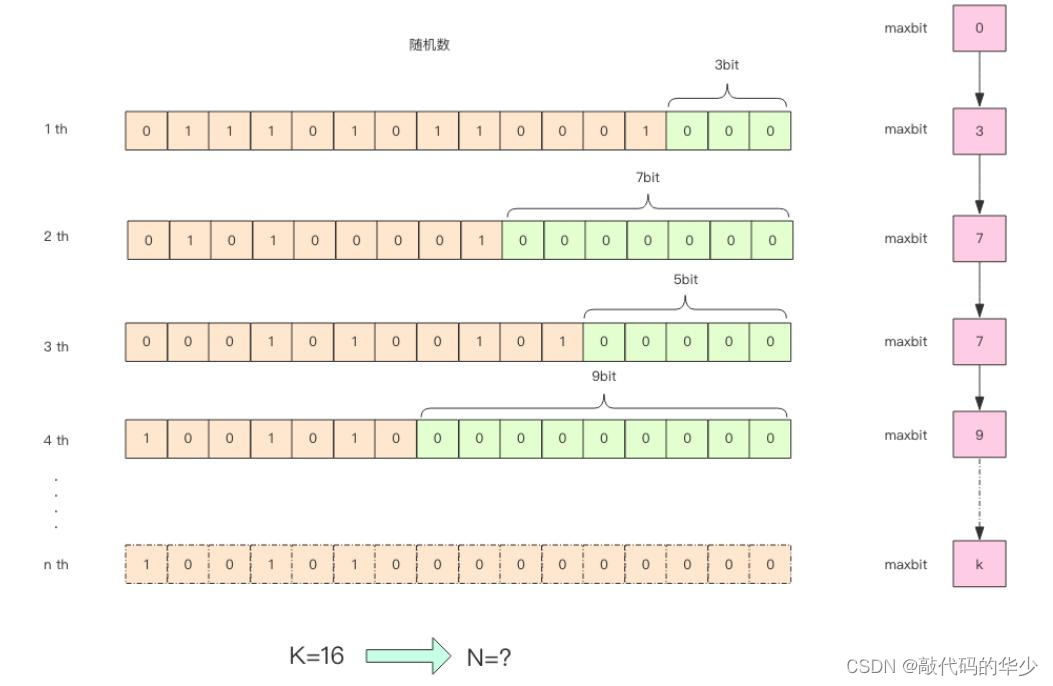
这张图的意思是，我们给定一系列的随机整数，记录下低位连续零位的最大长度 K，即为图中的 maxbit，通过这个 K 值我们就可以估算出随机数的数量 N。

任何值在计算机中我们都可以将其转换为比特串，也就是0和1组成的bit数组，我们从这个bit串的低位开始计算，直到出现第一个1为止，这就好比上面的伯努利试验抛硬币，一直抛硬币直到出现第一个正面为止（只是这里是数字0和1，伯努利试验中使用的硬币的正与反，并没有区别）。而HyperLogLog估算的随机数的数量，比如我们统计的UV，就好比伯努利试验中试验的次数。

那么估算方法是如何和下面的问题联系上的呢？

统计页面每天有多少用户点击的次数。同一个用户的反复点击进入记为 1 次

HyperLogLog的实现主要分为以下几个步骤：

1、转为比特串

通过hash函数，将输入的数据转换为比特串，例如输入5，便转为：101。那么为什么要这样转化呢？

是因为要和抛硬币对应上，比特串中，0 代表了反面，1 代表了正面，如果一个数据最终被转化了 10010000，那么从右往左，从低位往高位看，我们可以认为，首次出现 1 的时候，就是正面。

那么基于上面的估算结论，我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验，同样也就可以根据存入数据中，转化后的出现了 1 的最大的位置 k_max 来估算存入了多少数据。

2、分桶
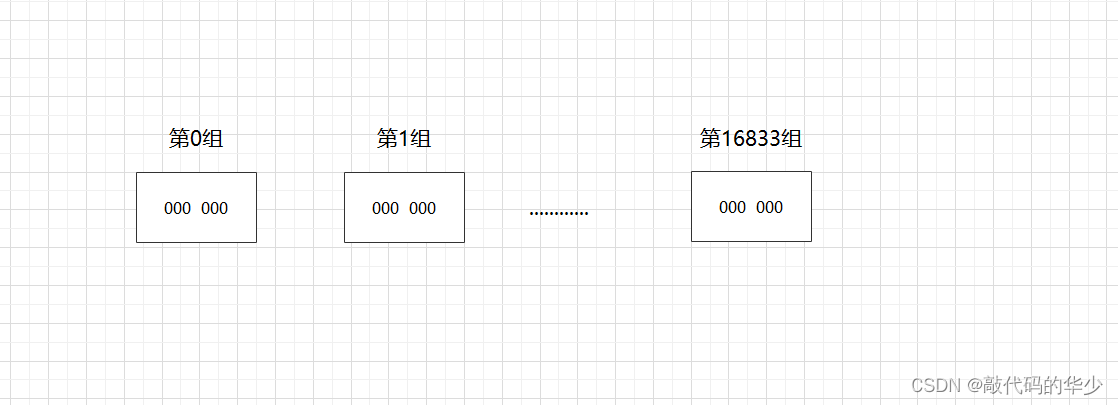
分桶就是分多少轮。抽象到计算机存储中去，这样做的的好处可以使估值更加准确，分桶通过一个单位是bit，长度为 L 的大数组 S ，将 数组 S 平均分为 m 组，注意这个 m 组，就是对应多少轮，然后每组所占有的比特个数是平均的，设为 P。得出如下关系：

• L = S.length
• L = m * p
• 以 K 为单位，S 占用的内存 = L / 8 / 1024

在 HyperLogLog中，HyperLogLog设置为：m=16834，p=6，L=16834 * 6。占用内存为=16834 * 6 / 8 / 1024 = 12K，那么这里为何是6位来存储kmax，因为6位可以存储的最大值为64，现在计算机都是64位或32位操作系统，因此6位最节省内存，又能满足需求。

形象化为：

3、对应
每个用户对应了一个id，不同的用户 id 标识了一个用户，那么我们可以把用户的 id 作为被hash的输入，如下：

hash(id) = 比特串

不同的用户 id，必然拥有不同的比特串。每一个比特串，也必然会至少出现一次 1 的位置。我们类比每一个比特串为一次伯努利试验。

现在要分轮，也就是分桶。所以我们可以设定，每个比特串的前多少位转为10进制后，其值就对应于所在桶的标号。假设比特串的低两位用来计算桶下标志，此时有一个用户的id的比特串是：1001011000011。它的所在桶下标为：11(2) = 12^1 + 12^0 = 3，处于第3个桶，即第3轮中。

上面例子中，计算出桶号后，剩下的比特串是：10010110000，从低位到高位看，第一次出现 1 的位置是 5 。也就是说，此时第3个桶，第3轮的试验中，k_max = 5。5 对应的二进制是：101，又因为每个桶有 p 个比特位。当 p>=3 时，便可以将 101 存进去。

模仿上面的流程，多个不同的用户 id，就被分散到不同的桶中去了，且每个桶有其 k_max。然后当要统计出 mian 页面有多少用户点击量的时候，就是一次估算。最终结合所有桶中的 k_max，代入估算公式，便能得出估算值。

代码实现-伯努利试验

简单编写代码做一个实验，来探究一下 K 和 N 之间的关系：

/*** <p>*      伯努利试验 中基数n与kmax之间的关系  n = 2^kmax* </p>** @Author: Why*/
public class PfHyperLogLogTest {staticclass BitKeeper {//记录最大的低位0的长度private int maxbit;//该方法生成随机数public void random() {long value = ThreadLocalRandom.current().nextLong(2L << 32);int bit = lowZeros(value);if (bit > this.maxbit) {this.maxbit= bit;}}//value >> i 表示将value右移i,  1<= i <32 ， 低位会被移出//value << i 表示将value左移i,  1<= i <32 ， 低位补0private int lowZeros(long value) {int i = 0;for (; i < 32; i++) {if (value >> i << i != value) {break;}}return i - 1;}}staticclass Experiment {//测试次数Nprivate int n;private BitKeeper keeper;public Experiment(int n) {this.n = n;this.keeper = new BitKeeper();}public void work() {for (int i = 0; i < n; i++) {this.keeper.random();}}//输出每一轮测试次数n//输出 logn / log2 = k 得 2^k = n，这里的k即我们估计的kmax//输出 kmax，低位最大0位长度值public void debug() {System.out.printf("%d %.2f %d\n", this.n, Math.log(this.n) / Math.log(2), this.keeper.maxbit);}}public static void main(String[] args) {for (int i = 1000; i < 100000; i += 100) {Experiment exp = new Experiment(i);exp.work();exp.debug();}}
}

截取部分数据查看：

3400015.0513
3500015.1013
3600015.1416
3700015.1817
3800015.2114
3900015.2516
4000015.2914
4100015.3216
4200015.3618

可以发现 K 和 N 的对数之间存在显著的线性相关性：N 约等于 2k

代码实现-HyperLogLog

根据HyperLogLog中采用调和平均数+分桶的方式来做代码优化，真实的 HyperLogLog 要比上面的示例代码更加复杂一些，也更加精确一些，这里做简单点的HyperLogLog算法的实现，代码如下：

publicclass PfTest {staticclass BitKeeper {// 无变化, 代码省略}staticclass Experiment {privateint n;privateint k;private BitKeeper[] keepers;public Experiment(int n) {this(n, 1024);}public Experiment(int n, int k) {this.n = n;this.k = k;this.keepers = new BitKeeper[k];for (int i = 0; i < k; i++) {this.keepers[i] = new BitKeeper();}}public void work() {for (int i = 0; i < this.n; i++) {long m = ThreadLocalRandom.current().nextLong(1L << 32);BitKeeper keeper = keepers[(int) (((m & 0xfff0000) >> 16) % keepers.length)];keeper.random();}}//估算 ，求倒数的平均数，调和平均数public double estimate() {double sumbitsInverse = 0.0;for (BitKeeper keeper : keepers) {sumbitsInverse += 1.0 / (float) keeper.maxbit;}double avgBits = (float) keepers.length / sumbitsInverse;return Math.pow(2, avgBits) * this.k;}}public static void main(String[] args) {for (int i = 100000; i < 1000000; i += 100000) {Experiment exp = new Experiment(i);exp.work();double est = exp.estimate();System.out.printf("%d %.2f %.2f\n", i, est, Math.abs(est - i) / i);}}
}

观察打印日志输出，误差率百分比控制在个位数：

10000094274.940.06
200000194092.620.03
300000277329.920.08
400000373281.660.07
500000501551.600.00
600000596078.400.01
700000687265.720.02
800000828778.960.04
900000944683.530.05

真实的 HyperLogLog

这里有个网站可以动态地让你看到 HyperLogLog 的算法到底是怎么执行的。

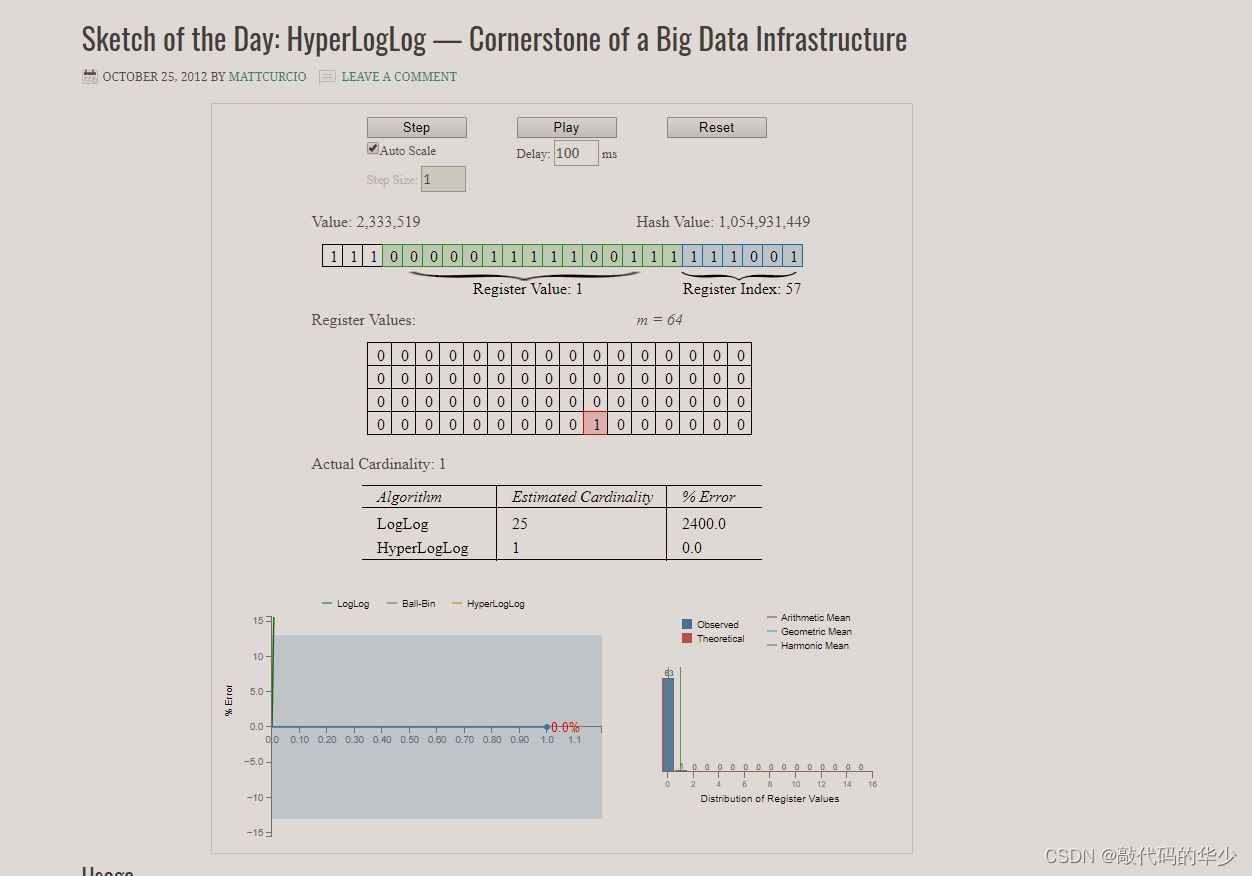
这里解释一下几个概念：

• m 表示分桶个数： 从图中可以看到，这里分成了 64 个桶
• 蓝色的 bit 表示在桶中的位置： 例如图中的 101110 实则表示二进制的 46，所以该元素被统计在中间大表格 Register Values 中标红的第 46 个桶之中
• 绿色的 bit 表示第一个 1 出现的位置：从图中可以看到标绿的 bit 中，从右往左数，第一位就是 1，所以在 Register Values 第 46 个桶中写入 1
• 红色 bit 表示绿色 bit 的值的累加： 下一个出现在第 46 个桶的元素值会被累加

为什么要统计 Hash 值中第一个 1 出现的位置？

因为第一个 1 出现的位置可以同我们抛硬币的游戏中第一次抛到正面的抛掷次数对应起来，根据上面掷硬币实验的结论，记录每个数据的第一个出现的位置 K，就可以通过其中最大值 Kmax 来推导出数据集合中的基数：N = 2Kmax

PF 的内存占用为什么是 12 KB？

我们上面的算法中使用了 1024 个桶，网站演示也只有 64 个桶，不过在 Redis 的 HyperLogLog 实现中，用的是 16384 个桶，即：214，也就是说，就像上面网站中间那个 Register Values 大表格有 16384 格。

而Redis 最大能够统计的数据量是 264，即每个桶的 maxbit 需要 6 个 bit 来存储，最大可以表示 maxbit = 63，于是总共占用内存就是：(214) x 6 / 8 (每个桶 6 bit，而这么多桶本身要占用 16384 bit，再除以 8 转换成 KB),算出来的结果就是 12 KB。

Redis 中的 HyperLogLog 实现

从上面我们算是对 HyperLogLog 的算法和思想有了一定的了解,我们知道一个HyperLogLog实际占用的空间大约是 13684 * 6bit / 8 = 12k 字节。但是在计数比较小的时候，大多数桶的计数值都是零。如果 12k 字节里面太多的字节都是零，那么这个空间是可以适当节约一下的。Redis 在计数值比较小的情况下采用了稀疏存储，稀疏存储的空间占用远远小于 12k 字节。相对于稀疏存储的就是密集存储，密集存储会恒定占用 12k 字节。

密集存储结构

不论是稀疏存储还是密集存储，Redis 内部都是使用字符串位图来存储 HyperLogLog 所有桶的计数值。密集存储的结构非常简单，就是连续 16384 个 6bit 串成的字符串位图。

那么给定一个桶编号，如何获取它的 6bit 计数值呢？这 6bit 可能在一个字节内部，也可能会跨越字节边界。我们需要对这一个或者两个字节进行适当的移位拼接才可以得到计数值。

假设桶的编号为idx，这个 6bit 计数值的起始字节位置偏移用 offset_bytes表示，它在这个字节的起始比特位置偏移用 offset_bits 表示。我们有:

offset_bytes = (index * 6) / 8
offset_bits = (index * 6) % 8

前者是商，后者是余数。比如 bucket 2 的字节偏移是 1，也就是第 2 个字节。它的位偏移是4，也就是第 2 个字节的第 5 个位开始是 bucket 2 的计数值。需要注意的是字节位序是左边低位右边高位，而通常我们使用的字节都是左边高位右边低位，我们需要在脑海中进行倒置。

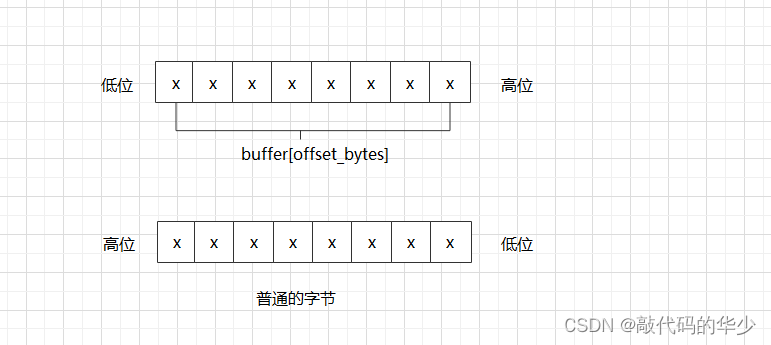
这里就涉及到两种情况，如果 offset_bits 小于等于 2，说明这 6 bit 在一个字节的内部，可以直接使用下面的表达式得到计数值 val：

val = buffer[offset_bytes] >> offset_bits # 向右移位

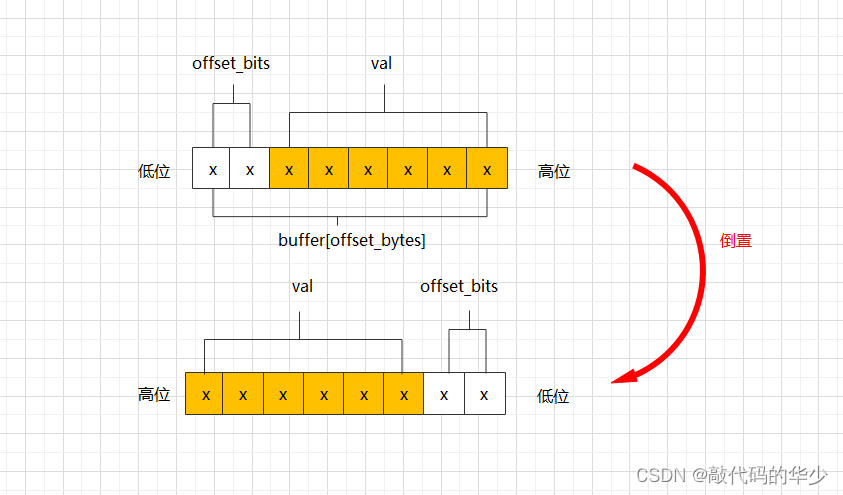
如果 offset_bits 大于 2，那么就会跨越字节边界，这时需要拼接两个字节的位片段。

# 低位值
low_val = buffer[offset_bytes] >> offset_bits
# 低位个数
low_bits = 8 - offset_bits
# 拼接，保留低6位
val = (high_val << low_bits | low_val) & 0b111111

不过下面 Redis 的源码要晦涩一点，看形式它似乎只考虑了跨越字节边界的情况。这是因为如果 6bit 在单个字节内，上面代码中的 high_val 的值是零，所以这一份代码可以同时照顾单字节和双字节。

// 获取指定桶的计数值
#define HLL_DENSE_GET_REGISTER(target,p,regnum) do { \uint8_t *_p = (uint8_t*) p; \unsigned long _byte = regnum*HLL_BITS/8; \unsignedlong _fb = regnum*HLL_BITS&7; \  # %8 = &7unsignedlong _fb8 = 8 - _fb; \unsignedlong b0 = _p[_byte]; \unsignedlong b1 = _p[_byte+1]; \target = ((b0 >> _fb) | (b1 << _fb8)) & HLL_REGISTER_MAX; \
} while(0)// 设置指定桶的计数值
#define HLL_DENSE_SET_REGISTER(p,regnum,val) do { \uint8_t *_p = (uint8_t*) p; \unsigned long _byte = regnum*HLL_BITS/8; \unsigned long _fb = regnum*HLL_BITS&7; \unsigned long _fb8 = 8 - _fb; \unsigned long _v = val; \_p[_byte] &= ~(HLL_REGISTER_MAX << _fb); \_p[_byte] |= _v << _fb; \_p[_byte+1] &= ~(HLL_REGISTER_MAX >> _fb8); \_p[_byte+1] |= _v >> _fb8; \
} while(0)

稀疏存储结构

Redis真的会用16384个6bit存储每一个HyperLogLog对象？，显然不会，虽然它只占用了12K内存，但是Redis对于内存的节约已经到了丧心病狂的地步了。因此，如果比较多的计数值都是0，那么就会采用稀疏存储的结构。

当多个连续桶的计数值都是零时，Redis 使用了一个字节来表示接下来有多少个桶的计数值都是零：00xxxxxx。前缀两个零表示接下来的 6bit 整数值加 1 就是零值计数器的数量，注意这里要加 1 是因为数量如果为零是没有意义的。比如 00010101表示连续 22 个零值计数器。6bit 最多只能表示连续 64 个零值计数器，所以 Redis 又设计了连续多个多于 64 个的连续零值计数器，它使用两个字节来表示：01xxxxxx yyyyyyyy，后面的 14bit 可以表示最多连续 16384 个零值计数器。这意味着 HyperLogLog 数据结构中 16384 个桶的初始状态，所有的计数器都是零值，可以直接使用 2 个字节来表示。

如果连续几个桶的计数值非零，那就使用形如 1vvvvvxx 这样的一个字节来表示。中间 5bit 表示计数值，尾部 2bit 表示连续几个桶。它的意思是连续 （xx +1） 个计数值都是 （vvvvv + 1）。比如 10101011 表示连续 4 个计数值都是 11。注意这两个值都需要加 1，因为任意一个是零都意味着这个计数值为零，那就应该使用零计数值的形式来表示。注意计数值最大只能表示到32，而 HyperLogLog 的密集存储单个计数值用 6bit 表示，最大可以表示到 63。当稀疏存储的某个计数值需要调整到大于 32 时，Redis 就会立即转换 HyperLogLog 的存储结构，将稀疏存储转换成密集存储。

Redis用三条指令来表达稀疏存储的方式：

• ZERO:len 单个字节表示 00[len-1]，连续最多64个零计数值
• VAL:value,len 单个字节表示 1[value-1][len-1]，连续 len 个值为 value 的计数值
• XZERO:len 双字节表示 01[len-1]，连续最多16384个零计数值

#define HLL_SPARSE_XZERO_BIT 0x40 /* 01xxxxxx */
#define HLL_SPARSE_VAL_BIT 0x80 /* 1vvvvvxx */
#define HLL_SPARSE_IS_ZERO(p) (((*(p)) & 0xc0) == 0) /* 00xxxxxx */
#define HLL_SPARSE_IS_XZERO(p) (((*(p)) & 0xc0) == HLL_SPARSE_XZERO_BIT)
#define HLL_SPARSE_IS_VAL(p) ((*(p)) & HLL_SPARSE_VAL_BIT)
#define HLL_SPARSE_ZERO_LEN(p) (((*(p)) & 0x3f)+1)
#define HLL_SPARSE_XZERO_LEN(p) (((((*(p)) & 0x3f) << 8) | (*((p)+1)))+1)
#define HLL_SPARSE_VAL_VALUE(p) ((((*(p)) >> 2) & 0x1f)+1)
#define HLL_SPARSE_VAL_LEN(p) (((*(p)) & 0x3)+1)
#define HLL_SPARSE_VAL_MAX_VALUE 32
#define HLL_SPARSE_VAL_MAX_LEN 4
#define HLL_SPARSE_ZERO_MAX_LEN 64
#define HLL_SPARSE_XZERO_MAX_LEN 16384

上图使用指令形式表示如下：

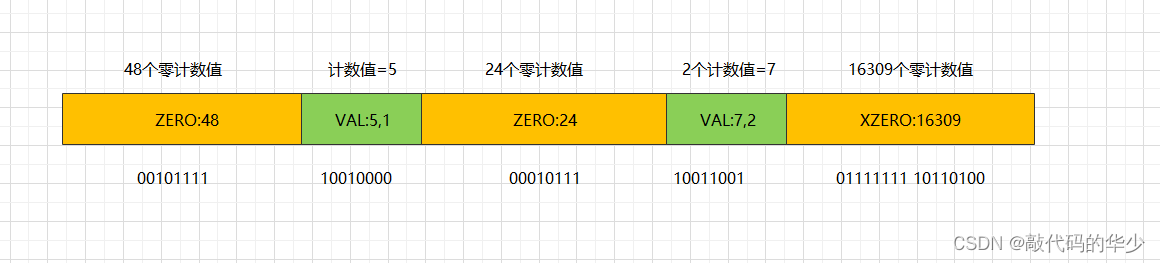
存储转换

• 任意一个计数值从 32 变成 33，因为VAL指令已经无法容纳，它能表示的计数值最大为 32
• 稀疏存储占用的总字节数超过 3000 字节，这个阈值可以通过 hll_sparse_max_bytes 参数进行调整

对象头

HyperLogLog 除了需要存储 16384 个桶的计数值之外，它还有一些附加的字段需要存储，比如总计数缓存、存储类型。所以它使用了一个额外的对象头来表示。

struct hllhdr {char magic[4];      /* 魔术字符串"HYLL" */uint8_t encoding;   /* 存储类型 HLL_DENSE or HLL_SPARSE. */uint8_t notused[3]; /* 保留三个字节未来可能会使用 */uint8_t card[8];    /* 总计数缓存 */uint8_t registers[]; /* 所有桶的计数器 */
};

所以 HyperLogLog 整体的内部结构就是 HLL 对象头 加上 16384 个桶的计数值位图。它在 Redis 的内部结构表现就是一个字符串位图。你可以把 HyperLogLog 对象当成普通的字符串来进行处理。

127.0.0.1:6379> pfadd codehole python java golang
(integer) 1
127.0.0.1:6379> get codehole
"HYLL\x01\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x80C\x03\x84MK\x80P\xb8\x80^\xf3"
但是不可以使用 HyperLogLog 指令来操纵普通的字符串，因为它需要检查对象头魔术字符串是否是 "HYLL"。127.0.0.1:6379> set codehole python
OK
127.0.0.1:6379> pfadd codehole java golang
(error) WRONGTYPE Key is not a valid HyperLogLog string value.

但是如果字符串以 “HYLL\x00” 或者 “HYLL\x01” 开头，那么就可以使用 HyperLogLog 的指令。

127.0.0.1:6379> set codehole "HYLL\x01whatmagicthing"
OK
127.0.0.1:6379> get codehole
"HYLL\x01whatmagicthing"
127.0.0.1:6379> pfadd codehole python java golang
(integer) 1

也许你会感觉非常奇怪，这是因为 HyperLogLog 在执行指令前需要对内容进行格式检查，这个检查就是查看对象头的 magic 魔术字符串是否是 “HYLL” 以及 encoding 字段是否是 HLL_SPARSE=0 或者 HLL_DENSE=1 来判断当前的字符串是否是 HyperLogLog 计数器。如果是密集存储，还需要判断字符串的长度是否恰好等于密集计数器存储的长度。

int isHLLObjectOrReply(client *c, robj *o) {.../* Magic should be "HYLL". */if (hdr->magic[0] != 'H' || hdr->magic[1] != 'Y' ||hdr->magic[2] != 'L' || hdr->magic[3] != 'L') goto invalid;if (hdr->encoding > HLL_MAX_ENCODING) goto invalid;if (hdr->encoding == HLL_DENSE &&stringObjectLen(o) != HLL_DENSE_SIZE) goto invalid;return C_OK;invalid:addReplySds(c,sdsnew("-WRONGTYPE Key is not a valid ""HyperLogLog string value.\r\n"));return C_ERR;
}