3、电路综合原理与实践---单双端口理想微带线（伪）手算S参数与时域波形

本文主要是介绍3、电路综合原理与实践---单双端口理想微带线（伪）手算S参数与时域波形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

电路综合原理与实践—单双端口理想微带线（伪）手算S参数与时域波形与时域波形

1、单理想微带线（UE）的S参数理论推导

参考：Design of Ultra Wideband Power Transfer Networks的第四章，之后总结推导过程

自己总结的参考过程推导理论：
单微带线手算S参数理论

2、推导模型

在此举一个简单的示例，其中源阻抗为30欧姆，微带线阻抗为10欧姆，负载阻抗为50欧姆：
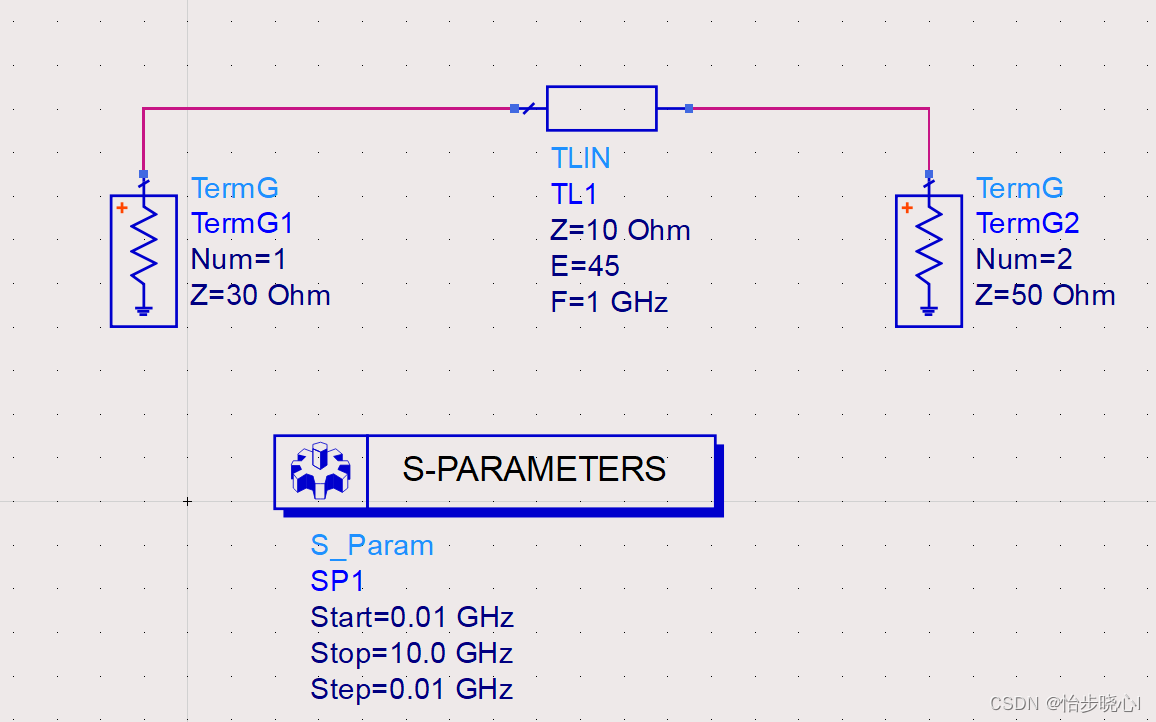
在这里插入图片描述

3、频域散射参数推导计算公式

所有用到的公式都在Design of Ultra Wideband Power Transfer Networks的第四章中有完整的推导：

clear
close all
%微带线电长度
ele_l=45;
%微带线电长度所在的频率
f=1e9;
%源阻抗
R1=30;
%负载阻抗
R2=50;
%微带线特性阻抗
Z0=10;
%求解频率范围，单位GHz
f_start=0.01;
f_stop=10;
f_step=0.01;%光速
c=299792458;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度，单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);C1=Z0*(R1+R2);
D1=Z0*Z0+R1*R2;
S11=(Z0*(R2-R1)+(Z0*Z0-R1*R2)*lamda)./(C1+D1*lamda);
S21=sqrt(R1)/sqrt(R2)*Z0*(R2+Z0)*(1+(R2-Z0)/(R2+Z0))*sqrt(1-lamda.*lamda)./(C1+D1*lamda);figure
plot(freq_solve/1e9,20*log10(abs(S11)))
xlabel('Frequency(GHz)')
ylabel('dB(S11)')
title('S11')figure
plot(freq_solve/1e9,20*log10(abs(S21)))
xlabel('Frequency(GHz)')
ylabel('dB(S21)')
title('S21')

Matlab的理论运行结果如下所示：
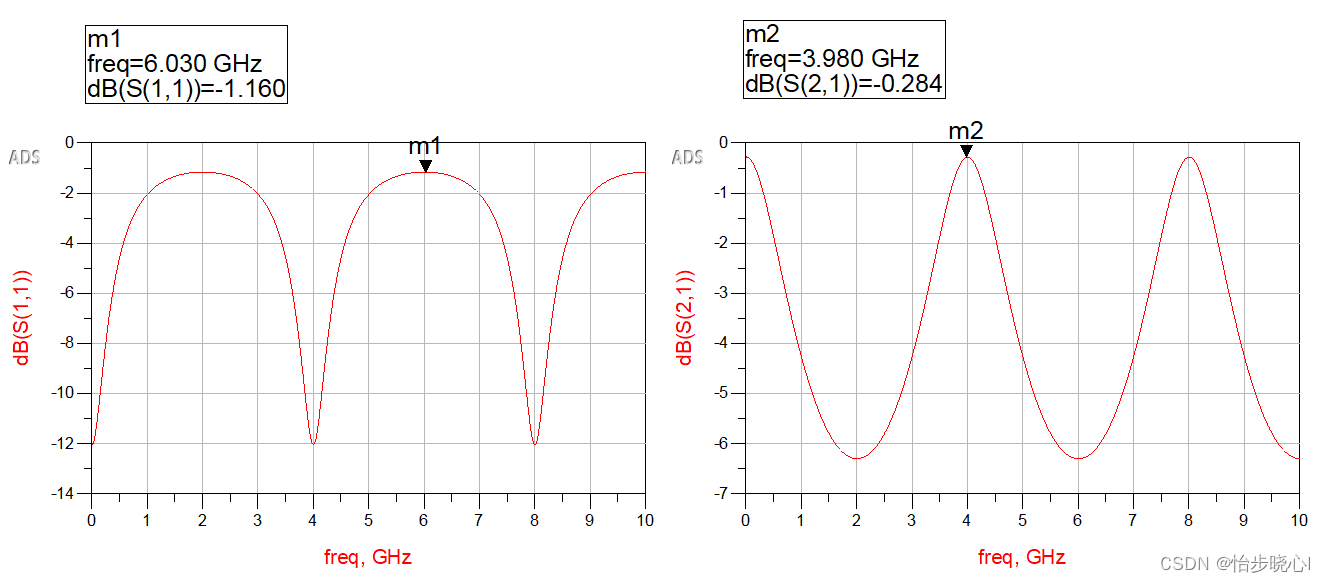
在这里插入图片描述
ADS仿真的对比结果如下所示，可见完全一致：

4、时域波形推导计算公式

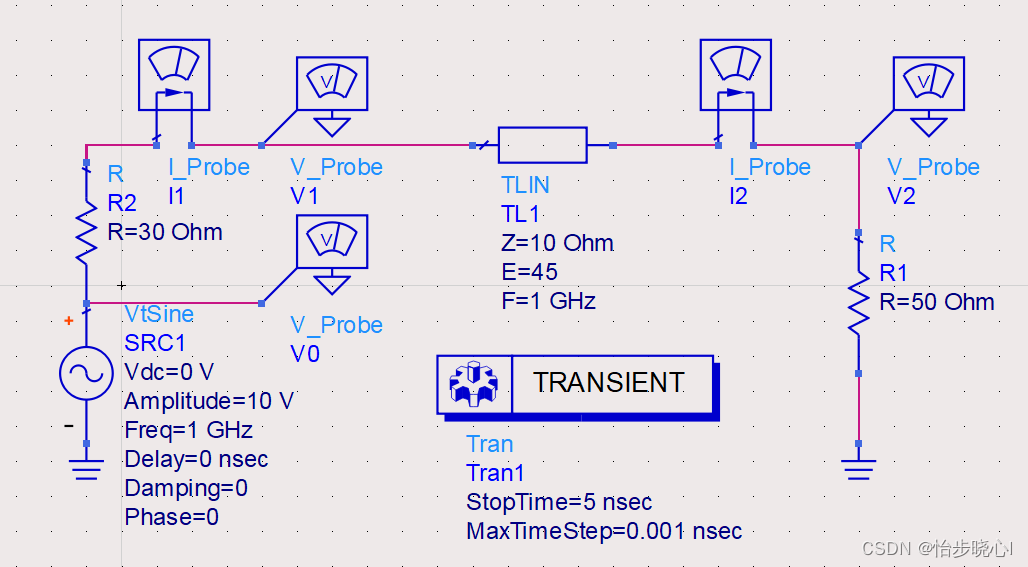
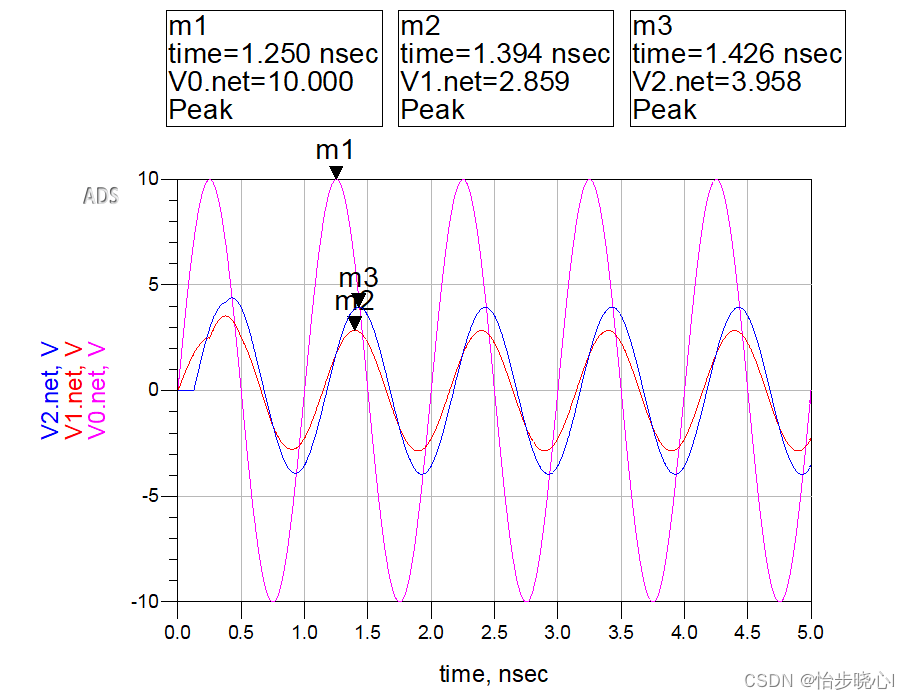
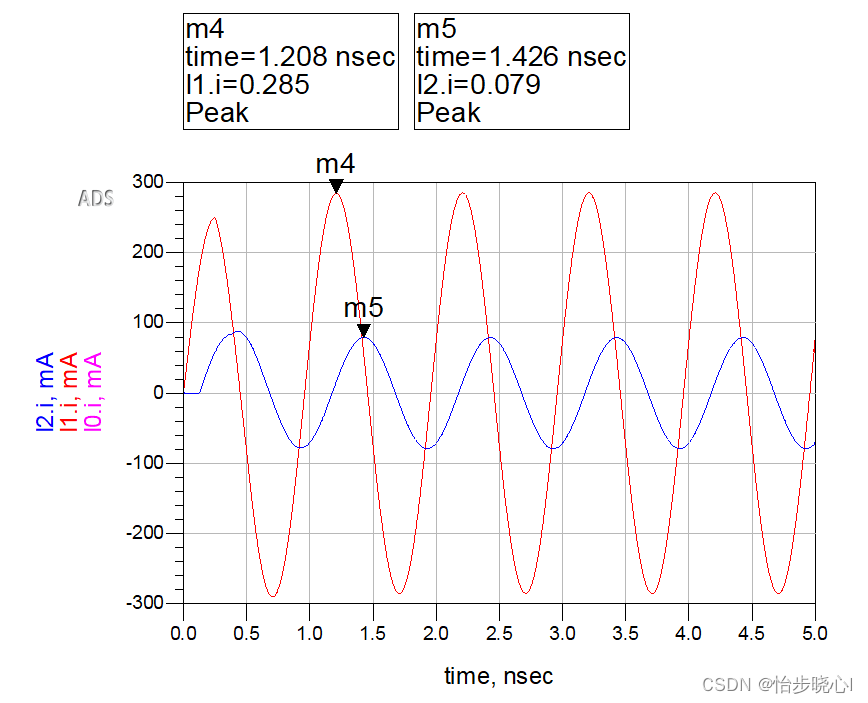
推导所使用的ADS模型，其中输入的正弦波激励的峰峰值为10V，V1和I1为输入电压电流，V2和I2为输出电压电流：
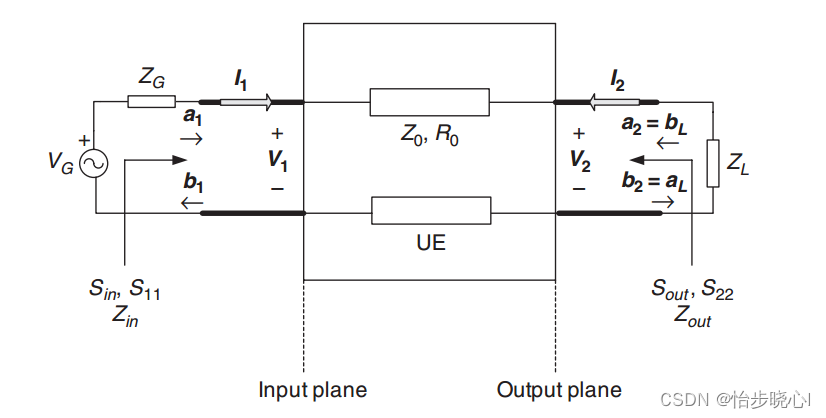
在这里插入图片描述
对应的理论模型如下所示：

所有用到的公式都在Design of Ultra Wideband Power Transfer Networks的第四章中有完整的推导：

clear
close all
clc
%微带线电长度
ele_l=45;
%微带线电长度所在的频率
f=1e9;
%源阻抗
R1=30;
%负载阻抗
R2=50;
%微带线特性阻抗
Z0=10;
%求解频率范围，单位GHz
f_start=1;
f_stop=1;
f_step=0.01;%光速
c=299792458;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度，单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);C1=Z0*(R1+R2);
D1=Z0*Z0+R1*R2;
S11=(Z0*(R2-R1)+(Z0*Z0-R1*R2)*lamda)./(C1+D1*lamda);
S21=sqrt(R1)/sqrt(R2)*Z0*(R2+Z0)*(1+(R2-Z0)/(R2+Z0))*sqrt(1-lamda.*lamda)./(C1+D1*lamda);%激励信号幅度
VG=10;
%入射波A和反射波B
A=VG/2*Z0*(R2+Z0)*sqrt(1-lamda.*lamda)./(C1+D1*lamda);
B=VG/2*Z0*(R2-Z0)*sqrt(1-lamda.*lamda)./(C1+D1*lamda);
%计算1端口的电压电流
I1=VG*(Z0+R2*lamda)./(C1+D1*lamda);
V1=VG*(Z0*R2+Z0*Z0*lamda)./(C1+D1*lamda);
a1=VG/sqrt(R1);
b1=VG/sqrt(R1)*(Z0*(R2-R1)+(Z0*Z0-R1*R2)*lamda)./(C1+D1*lamda);
%计算2端口的电压电流
b2=VG/sqrt(R2)*Z0*(R2+Z0)*(1+(R2-Z0)/(R2+Z0))*sqrt(1-lamda.*lamda)./(C1+D1*lamda);
V2=b2/2*sqrt(R2);
I2=-V2/R2;
a2=V2/sqrt(R2)+sqrt(R2)*I2;disp(['端口1电压幅值为',num2str(abs(V1)),',端口1电压相位为',num2str(phase(V1)),',与激励信号相比相差',num2str(1e9*(phase(V1)/(2*pi)*1/freq_solve)),'ns'])
disp(['端口1电流幅值为',num2str(abs(I1)),',端口1电流相位为',num2str(phase(I1)),',与激励信号相比相差',num2str(1e9*(phase(I1)/(2*pi)*1/freq_solve)),'ns'])disp(['端口2电压幅值为',num2str(abs(V2)),',端口1电压相位为',num2str(phase(V2)),',与激励信号相比相差',num2str(1e9*(phase(V2)/(2*pi)*1/freq_solve)),'ns'])
disp(['端口2电流幅值为',num2str(abs(I2)),',端口1电流相位为',num2str(phase(I2)),',与激励信号相比相差',num2str(1e9*(phase(V2)/(2*pi)*1/freq_solve)),'ns'])

运行结果如下所示（都是和输入电压的相位作为比较）：
在这里插入图片描述
对比一下ADS仿真结果（值得注意的是，此处Matlab求解得到的只是稳态解，然而ADS仿真得到的1ns内电路还没有进入到稳态，或许可以理解为电磁波还没有传输到终端或者入射波和反射波还没有叠加上，但是我还没有研究这种时域分析是如何进行的）：
在这里插入图片描述