潜在结果框架(Potential outcomes)与工具变量(Instrumental variable)介绍

本文主要是介绍潜在结果框架(Potential outcomes)与工具变量(Instrumental variable)介绍，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Potential outcomes framework

什么是potential outcome呢？考虑在医学中，X=0表示不吃药，X=1表示吃药，那么很显然，一个人是没有办法同时吃药与不吃药的，所以我们只能够观测到其中的一个结果，即 $\displaystyle Y( 0)$ 或 $\displaystyle Y( 1)$ ，而X只是用于选择观测的结果。

在这里插入图片描述

然而每个人对于吃药的结果是有可能不同的，比如有的人不管吃不吃都没法变好，有的人吃了就能恢复了，有的人吃了反而更难受了，还有的不管吃不吃都能恢复，对应着以下四类。

在这里插入图片描述

可记为

$NR)\\ P( Y( 0) =0,Y( 1) =1) =P( HE)\\ P( Y( 0) =1,Y( 1) =0) =P( HU)\\ P( Y( 0) =1,Y( 1) =1) =P( AR)$

基于上面的各种情况，我们用Average Causal Effect(ACE)计算的因果效应将是：

$\begin{aligned} ACE\left( X\rightarrow Y\right) & \equiv E[ Y( 1) -Y( 0)]\\ & =0*P( NR) +1*P( HE) +0*P( HU) +1*P( AR)\\ & -( 0*P( NR) +0*P( HE) +1*P( HU) +1*P( AR))\\ & =P( HE) +P( AR) -P( HU) -P( AR)\\ & =P( HE) -P( HU) \in [ -1,1] \end{aligned}$

从随机试验估计ACE

那么ACE能不能从样本总估计呢？当满足ignorebility的时候就可以：

$X\bot Y( 0) ,\ X\bot Y( 1)$

于是

$Y=y|X=0)\\ P( Y( 1) =y) =P( Y( 1) =y|X=1) =P( Y=y|X=1)$

此外
$\begin{aligned} P( Y( 0) =0) =\sum _{y} P( Y( 0) =0,Y( 1) =y) =P( NR) +P( HE) =P( Y=0|X=0) \\ P( Y( 0) =1) =\sum _{y} P( Y( 0) =1,Y( 1) =y) =P( HU) +P( AR) =P( Y=1|X=0)\\ P( Y( 1) =0) =\sum _{y} P( Y( 0) =y,Y( 1) =0) =P( NR) +P( HU) =P( Y=0|X=1) \\ P( Y( 1) =1) =\sum _{y} P( Y( 0) =y,Y( 1) =1) =P( HE) +P( AR) =P( Y=1|X=1) \end{aligned} \tag{1}$
注意上述等式，只有在满足ignorebility的时候才成立的，此时ACE可以用

$P (Y = 1 ∣ X = 1) - P (Y = 1 ∣ X = 0) = P (H E) - P (H U)$

得到。

反事实与随机试验

从上面的分析我们可以发现，我们只能从实验数据中得到4类人群比例的两两组合，却没有办法得到精确的 $\displaystyle P( NR) ,P( HE) ,P( HU) ,P( AR)$ 的值。

为什么我们需要在意他们每个人群的比例呢？直接算ACE不就好了？其实，ACE是一个“不太完善”的指标，因为ACE只是考虑的人群中的平均有效性，但忽略了那些会因为吃药而因此受伤的人，如果要正确的评价药效，那么我们应该用以下“完善”的指标：

$AR)\\ 不吃药收益=eP( NR) +fP( HE) +gP( HU) +hP( AR)$

其中a,b,c,d对应了每个不同人群下，吃药的收益，而e,f,g,h则是每一类人不吃药的收益，我们的目标是看看上述那个收益较大。显然，通过设置不同的收益，我们会有不同的决策。

但可惜的是，这是一个counterfatual问题，你是无法知道每一类人的比例的，为什么？不妨想想自己属于哪类人？你肯定无法给出答案，毕竟你无法同时知道自己吃药与不吃药后的状态，你只能观测其中一个。

所以我们观测的只是反事实的一小部分而已。

反事实与非随机试验（纯观测数据）

如果没有随机试验，这意味着ignobility是无法满足的，此时，我们没有办法从纯观测数据中得到正确的ACE了，那么我们能不能找到ACE的一个范围呢？考虑以下例子，

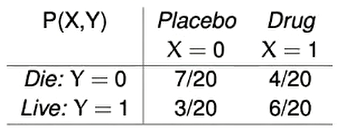
在这里插入图片描述

有的人使用了安慰剂，有的人使用了药，但是是否决定用药是非随机的。在这种情况下，我们尝试分析下， $\displaystyle P( HE)$ 和 $\displaystyle P( HU)$ 的最大值和最小值。

首先HE是吃了药才好，但不吃药就不好的人。首先 $\displaystyle P( Y=0|X=0)$ 里面可能有HE，也可能有NR，就是永远不好的人，另外， $\displaystyle P( Y=1|X=1)$ 中可能有HE，也可能有AR，即吃不吃药都好的人。因此 $\displaystyle P( HE)$ 的最大值就是当NR,AR都是0的时候，即
$max\ P( HE) =P( Y=0|X=0) +P( Y=1|X=1) =\frac{6+7}{20} =0.65$

那么HU的最小值是什么呢？类似的， $\displaystyle P( Y=1|X=0)$ 包含了AR和HU的人， $\displaystyle P( Y=0|X=1)$ 包含了NR和HU的人，那显然最小值就是这两拨人中，全是AR和NR的人了，于是

$min\ P( HU) =0$

从而 $\displaystyle max\ ACE=\frac{6+7}{20} -0$ .

类似的，

$min\ P( HE) =0\\ max\ P( HU) =\frac{4+3}{20} =0.35$

从而 $\displaystyle min\ ACE=0-\frac{4+3}{20}$ . 所以一个伤心的事实是，我们没有办法从纯观察数据中推断出ACE到底是正面还是负面的效果，他必然是经过0点的。

上面是一个比较直接的做法，我们可以尝试严格地证明一下这个bound。
首先，从上述的分析可以看出来，我们的观察数据本质上就是4个group中的人群的各种组合：
$\begin{aligned} P( X=0,Y=0) =\sum _{y} P( X=0,Y( 0) =0,Y( 1) =y) =P( X=0,NR) +P( X=0,HE) \\ P( X=0,Y=1) =\sum _{y} P( X=0,Y( 0) =1,Y( 1) =y) =P( X=0,HU) +P( X=0,AR)\\ P( X=1,Y=0) =\sum _{y} P( X=1,Y( 0) =y,Y( 1) =0) =P( X=1,NR) +P( X=1,HU) \\ P( X=1,Y=1) =\sum _{y} P( X=1,Y( 0) =y,Y( 1) =1) =P( X=1,HE) +P( X=1,AR) \end{aligned} \tag{2}$
对比公式(1)，我们就可以发现，由于X的取值不同会影响不同群体的人数，从而导致ACE的计算失效。我们还能发现

$\begin{aligned} & P( Y=0,X=0) +P( Y=1,X=1)\\ = & P( X=0,NR) +P( X=0,HE) +P( X=1,HE) +P( X=1,AR)\\ = & P( X=0,NR) +P( HE) +P( X=1,AR)\\ \geqslant & P( HE) \end{aligned}$

因此，类似的
$\begin{aligned} 0\leqslant HE\leqslant P( X=0,Y=0) +P( X=1,Y=1) \\ 0\leqslant HU\leqslant P( X=0,Y=1) +P( X=1,Y=0) \\ 0\leqslant NR\leqslant P( X=0,Y=0) +P( X=1,Y=0)\\ 0\leqslant AR\leqslant P( X=0,Y=1) +P( X=1,Y=1) \end{aligned} \tag{3}$
最后，回忆下，
$\begin{aligned} P( Y( x_{0}) =1) =P( HU) +P( AR)\\ P( Y( x_{1}) =1) =P( HE) +P( AR) \end{aligned} \tag{4}$
因此，结合公式(2),(4)，我们有
$\begin{aligned} P( X=0,Y=1) \leqslant P( Y( x_{0}) =1) \leqslant 1-P( X=0,Y=0)\\ P( X=1,Y=1) \leqslant P( Y( x_{1}) =1) \leqslant 1-P( X=1,Y=0) \end{aligned} \tag{5}$
根据公式(3)(5)的不等式，我们可以用图把他们画出来，在这里，我们来画一个三维图：

在这里插入图片描述

HE轴上的点表示所有人都是HE，HU轴上的点则表示所有人都是HU，AR轴上的点表示所有人都是AR，最后原点，表示所有人都是NR，因为此时AR,HE,HU都是0，所以都剩下NR了，也就是NR可以通过1-AR-HE-HU得到。

接下来，我们来计算一下这些bound：
$0\leqslant HE\leqslant P( X=0,Y=0) +P( X=1,Y=1) =\frac{7+6}{20}\\ 0\leqslant HU\leqslant P( X=0,Y=1) +P( X=1,Y=0) =\frac{3+7}{20}\\ 0\leqslant AR\leqslant P( X=0,Y=1) +P( X=1,Y=1) =\frac{3+6}{20}\\ \frac{3}{20} =P( X=0,Y=1) \leqslant P( HU) +P( AR) \leqslant 1-P( X=0,Y=0) =1-\frac{7}{20}\\ \frac{6}{20} =P( X=1,Y=1) \leqslant P( HE) +P( AR) \leqslant 1-P( X=1,Y=0) =1-\frac{4}{20}$

我们可以用Mathematica画出来看看：

RegionPlot3D[{y + z <= 1 - 7/20 && y + z >= 3/20 && x + z <= 1 - 4/20 && x + z >= 6/20}, {x, 0, (7 + 6)/20}, {y, 0, (7 + 3)/20}, {z, 0, (3 + 6)/20}, PlotPoints -> 100, Mesh -> None, AxesLabel -> {"HE", "HU", "AR"}, PlotStyle -> Directive[Yellow, Opacity[0.3]]]

在这里插入图片描述