本文主要是介绍BAAI 2020 北京智源大会 | 林伟 | Instrumental Variables for Multiple Causal Inference: Old and New,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Instrumental Variables for Multiple Causal Inference: Old and New
- 回放地址
- 报告内容
- 概述
- 主要内容
回放地址
林伟-Instrumental Variables for Multiple Causal Inference: Old and New
报告内容
概述
林伟研究员(北京大学研究员,智源学者)在本次talk中主要介绍了使用instrumental variables 来进行因果推理,通过设置一系列的assumption,将IV中的经典方法Two-stage least squares扩展到高维,并得到了很好的实验结果。
主要内容
研究者一直在诟病深度学习等里面的“黑箱”算法,我们怎么来理解我们模型中变量之间的因果机制,是一个非常重要的问题,尤其是对发展下一代AI来说。在下图中的例子中我们不知道是x造成了y,还是y造成了x,我们只能观察到x和y之间的联合分布。进一步说明multiple causal models can lead to the same prediction model

回顾了Judea Pearl提出的几个因果推理的工具。本次talk主要涉及到
- causal assumption 在你了解你的method之前这一部分是最critical的
- control confounding 这是因果推理中最难的一部分
- mediation analysis 本次talk中主要涉及区分direct effect 和indirect effect

在现代机器学习中我们不能仅仅关注一个简单cause 变量,我们需要关注多变量甚至是高纬度的cause变量。

介绍IV,就算是X对Y没有影响,但是由于U的存在,会使X和Y显得correlated。

继续介绍IV,目标是要把Two-stage least squares方法扩展到高维

IV的第三个条件是最苛刻的,我们能对它进行relax吗?

介绍了高纬度的instrumental variable,但是会引起biased,该如何解决?
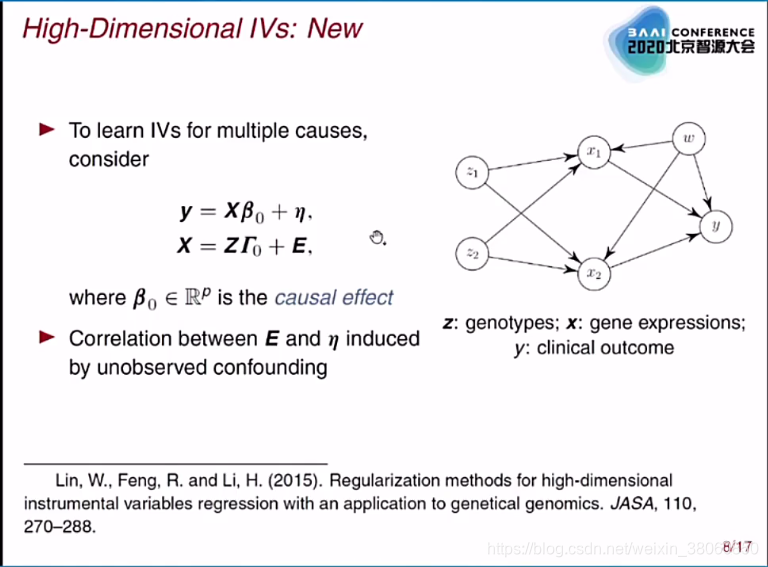
对IV的第三个assumption进行relax,但是又遇到了identifiability 的问题:因为Z在两个式子中都出现,无法分清Z和α的direct effect和indirect effect,应该怎么做?

将identifiability问题转换为解linear system,但是这个方程是不能解的,不过如果我们将solution假想成sparse,是能解的。从compressed sensing中借鉴了一些思想,变成structed compressed sensing problem。
![]()
又给了一个assumption,使得方程能够可解。

在前面得到identification的结果后,扩展Two-stage least squares方法来estimate我们感兴趣的参数。

给了相应的理论证明。

做了一些实验:如果identification问题能满足,那么我们的方法是最好的;如果不能满足,那么所有的方法都会fail。
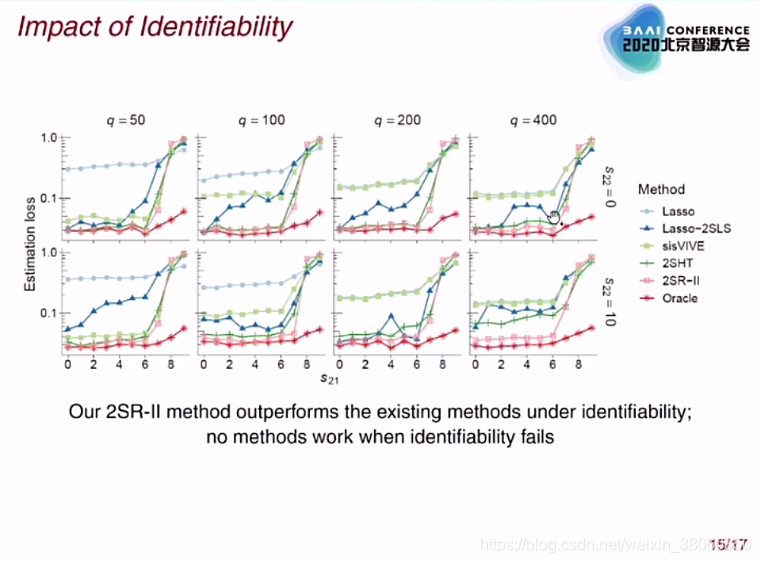
怎样将这些研究应用到真实的AI系统中呢?

这篇关于BAAI 2020 北京智源大会 | 林伟 | Instrumental Variables for Multiple Causal Inference: Old and New的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





