pta数据结构树和图实验题

2023-10-25 05:59
文章标签 数据结构 实验 pta 树和图

本文主要是介绍pta数据结构树和图实验题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

 先序输出叶结点 (15分)

本题要求按照先序遍历的顺序输出给定二叉树的叶结点。

函数接口定义：

void PreorderPrintLeaves( BinTree BT );

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;
};

函数PreorderPrintLeaves应按照先序遍历的顺序输出给定二叉树BT的叶结点，格式为一个空格跟着一个字符。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;
};BinTree CreatBinTree(); /* 实现细节忽略 */
void PreorderPrintLeaves( BinTree BT );int main()
{BinTree BT = CreatBinTree();printf("Leaf nodes are:");PreorderPrintLeaves(BT);printf("\n");return 0;
}
/* 你的代码将被嵌在这里 */

输出样例（对于图中给出的树）：

Leaf nodes are: D E H I

 

void PreorderPrintLeaves( BinTree BT )
{if(BT == NULL)return;//如果根节点为空，什么都不执行if(BT->Left == NULL && BT->Right == NULL)//如果一个节点既没有左孩子，又没有右孩子，说明是叶子节点 {printf(" %c", BT->Data);//题目要求：空格+字符 } PreorderPrintLeaves(BT->Left);//访问左孩子 PreorderPrintLeaves(BT->Right); //访问右孩子 
}

 

 

 邻接矩阵存储图的深度优先遍历 (20分)

试实现邻接矩阵存储图的深度优先遍历。

函数接口定义：

void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );

其中MGraph是邻接矩阵存储的图，定义如下：

typedef struct GNode *PtrToGNode;
struct GNode{int Nv;  /* 顶点数 */int Ne;  /* 边数   */WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */

函数DFS应从第V个顶点出发递归地深度优先遍历图Graph，遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时，要求按序号递增的顺序。题目保证V是图中的合法顶点。

裁判测试程序样例：

#include <stdio.h>typedef enum {false, true} bool;
#define MaxVertexNum 10  /* 最大顶点数设为10 */
#define INFINITY 65535   /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex;      /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;  /* 边的权值设为整型 */typedef struct GNode *PtrToGNode;
struct GNode{int Nv;  /* 顶点数 */int Ne;  /* 边数   */WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */MGraph CreateGraph(); /* 创建图并且将Visited初始化为false；裁判实现，细节不表 */void Visit( Vertex V )
{printf(" %d", V);
}void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );int main()
{MGraph G;Vertex V;G = CreateGraph();scanf("%d", &V);printf("DFS from %d:", V);DFS(G, V, Visit);return 0;
}/* 你的代码将被嵌在这里 */

输入样例：给定图如下

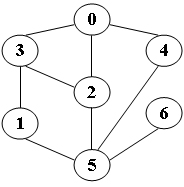
5

输出样例：

DFS from 5: 5 1 3 0 2 4 6

 

void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) )
{Visited[V] = true;//把当前节点标记为已访问 Visit(V);//输出当前节点 for(int i = 0; i < Graph->Nv; i++){if(Graph->G[V][i] == 1 && !Visited[i]){DFS(Graph, i, Visit);}}
}

 

邻接表存储图的广度优先遍历 (20分)

试实现邻接表存储图的广度优先遍历。

函数接口定义：

void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );

其中LGraph是邻接表存储的图，定义如下：

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{Vertex AdjV;        /* 邻接点下标 */PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};/* 顶点表头结点的定义 */
typedef struct Vnode{PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum];     /* AdjList是邻接表类型 *//* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  int Nv;     /* 顶点数 */int Ne;     /* 边数   */AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

函数BFS应从第S个顶点出发对邻接表存储的图Graph进行广度优先搜索，遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时，要求按邻接表顺序访问。题目保证S是图中的合法顶点。

裁判测试程序样例：

#include <stdio.h>typedef enum {false, true} bool;
#define MaxVertexNum 10   /* 最大顶点数设为10 */
typedef int Vertex;       /* 用顶点下标表示顶点,为整型 *//* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{Vertex AdjV;        /* 邻接点下标 */PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};/* 顶点表头结点的定义 */
typedef struct Vnode{PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum];     /* AdjList是邻接表类型 *//* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  int Nv;     /* 顶点数 */int Ne;     /* 边数   */AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */bool Visited[MaxVertexNum]; /* 顶点的访问标记 */LGraph CreateGraph(); /* 创建图并且将Visited初始化为false；裁判实现，细节不表 */void Visit( Vertex V )
{printf(" %d", V);
}void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );int main()
{LGraph G;Vertex S;G = CreateGraph();scanf("%d", &S);printf("BFS from %d:", S);BFS(G, S, Visit);return 0;
}/* 你的代码将被嵌在这里 */

输入样例：给定图如下

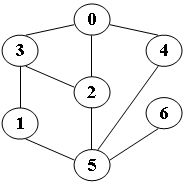
2

输出样例：

BFS from 2: 2 0 3 5 4 1 6

 

void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) )
{int que[1000];int f = 0, r = 0;que[r++] = S;Visit(S);Visited[S] = true;while(f != r){PtrToAdjVNode tmp = Graph->G[que[f++]].FirstEdge;while(tmp){Vertex pos = tmp->AdjV;if(!Visited[pos]){Visited[pos] = true;Visit(pos);que[r++] = pos;}tmp = tmp->Next;} }
}

 

二叉树的遍历 (25分)

本题要求给定二叉树的4种遍历。

函数接口定义：

void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;
};

要求4个函数分别按照访问顺序打印出结点的内容，格式为一个空格跟着一个字符。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;
};BinTree CreatBinTree(); /* 实现细节忽略 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );int main()
{BinTree BT = CreatBinTree();printf("Inorder:");    InorderTraversal(BT);    printf("\n");printf("Preorder:");   PreorderTraversal(BT);   printf("\n");printf("Postorder:");  PostorderTraversal(BT);  printf("\n");printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");return 0;
}
/* 你的代码将被嵌在这里 */

输出样例（对于图中给出的树）：

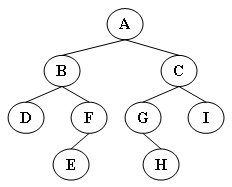
Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A
Levelorder: A B C D F G I E H
void InorderTraversal( BinTree BT )
{if(BT){InorderTraversal(BT->Left);printf(" %c", BT->Data);InorderTraversal(BT->Right);}
}
void PreorderTraversal( BinTree BT )
{if(BT){printf(" %c", BT->Data);PreorderTraversal(BT->Left);PreorderTraversal(BT->Right); }
}
void PostorderTraversal( BinTree BT )
{if(BT){PostorderTraversal(BT->Left);PostorderTraversal(BT->Right);printf(" %c", BT->Data);}
}
void LevelorderTraversal( BinTree BT )
{BinTree que[1000];int f = 0, r = 0;if(BT)que[r++] = BT;while(f != r){BinTree q = que[f++];printf(" %c", q->Data);if(q->Left)que[r++] = q->Left;if(q->Right)que[r++] = q->Right;}
}

 

树的遍历 (25分)

给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

 

 

#include<iostream>
using namespace std;
struct Node
{int data;Node* left;Node* right;
}*root;
int t;
int post[55], in[55];//输入的数组
void create(Node*& root, int l, int r)
{int flag = -1;for(int i = l; i <= r; i++){if(post[t] == in[i])//说明找到了根节点{flag = i;break;} }if(flag == -1)return;//没有找到根节点，什么也不执行root = new Node;root->data = in[flag];root->left = root->right = NULL;t--;//t保存的是后序的下标， 故--create(root->right, flag + 1, r);//已知中序和后序，先创建右子树，再创建左子树//已知前序和中序，先创建左子树，再创建右子树 create(root->left, l, flag - 1); } 
void level(Node* root)
{Node* que[1000];int f = 0, r = 0;if(root)que[r++] = root;while(f != r){Node* q = que[f++];if(f > 1)cout<<" ";//控制输出空格 cout<<q->data;if(q->left)que[r++] = q->left;if(q->right)que[r++] = q->right;}
}
int main()
{root = NULL;int n;cin>>n;t = n - 1;for(int i = 0; i < n; i++)cin>>post[i];for(int i = 0; i < n; i++)cin>>in[i];create(root, 0, n -1);level(root);return 0;
}

 

还原二叉树 (25分)

给定一棵二叉树的先序遍历序列和中序遍历序列，要求计算该二叉树的高度。

输入格式:

输入首先给出正整数N（≤50），为树中结点总数。下面两行先后给出先序和中序遍历序列，均是长度为N的不包含重复英文字母（区别大小写）的字符串。

输出格式:

输出为一个整数，即该二叉树的高度。

输入样例:

9
ABDFGHIEC
FDHGIBEAC

输出样例:

5

 

#include<iostream>
using namespace std;
struct Node
{int data;Node* left;Node* right;
}*root;
int t = 0;
char pre[55], in[55];//输入的数组
void create(Node*& root, int l, int r)
{int flag = -1;for(int i = l; i <= r; i++){if(pre[t] == in[i])//说明找到了根节点{flag = i;break;} }if(flag == -1)return;//没有找到根节点，什么也不执行root = new Node;root->data = in[flag];root->left = root->right = NULL;t++;//t保存的是前序的下标， 故++ create(root->left, l, flag - 1);create(root->right, flag + 1, r);//已知前序和中序，先创建左子树，再创建右子树 } 
int height(Node* root)
{if(root == NULL)return 0;int m = height(root->left);int n = height(root->right);return m > n ? m + 1 : n + 1;
}
int main()
{root = NULL;int n;cin>>n;cin>>pre>>in;create(root, 0, n -1);cout<<height(root)<<endl;return 0;
}

 

根据后序和中序遍历输出先序遍历 (25分)

本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果，输出该树的先序遍历结果。

输入格式:

第一行给出正整数N(≤30)，是树中结点的个数。随后两行，每行给出N个整数，分别对应后序遍历和中序遍历结果，数字间以空格分隔。题目保证输入正确对应一棵二叉树。

输出格式:

在一行中输出Preorder: 以及该树的先序遍历结果。数字间有1个空格，行末不得有多余空格。

输入样例:

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例:

Preorder: 4 1 3 2 6 5 7
#include<iostream>
using namespace std;
struct Node
{int data;Node* left;Node* right;
}*root;
int t;
int post[55], in[55];//输入的数组
void create(Node*& root, int l, int r)
{int flag = -1;for(int i = l; i <= r; i++){if(post[t] == in[i])//说明找到了根节点{flag = i;break;} }if(flag == -1)return;//没有找到根节点，什么也不执行root = new Node;root->data = in[flag];root->left = root->right = NULL;t--;create(root->right, flag + 1, r);create(root->left, l, flag - 1);	 } 
void Preorder(Node* root)
{if(root){printf(" %d", root->data);Preorder(root->left);Preorder(root->right);}
}
int main()
{root = NULL;int n;cin>>n;t = n - 1;for(int i = 0; i < n; i++)cin>>post[i];for(int i = 0; i < n; i++)cin>>in[i];create(root, 0, n -1);cout<<"Preorder:";Preorder(root);return 0;
}

 

 二叉搜索树的结构 (30分)

二叉搜索树或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。（摘自百度百科）

给定一系列互不相等的整数，将它们顺次插入一棵初始为空的二叉搜索树，然后对结果树的结构进行描述。你需要能判断给定的描述是否正确。例如将{ 2 4 1 3 0 }插入后，得到一棵二叉搜索树，则陈述句如“2是树的根”、“1和4是兄弟结点”、“3和0在同一层上”（指自顶向下的深度相同）、“2是4的双亲结点”、“3是4的左孩子”都是正确的；而“4是2的左孩子”、“1和3是兄弟结点”都是不正确的。

输入格式：

输入在第一行给出一个正整数N（≤100），随后一行给出N个互不相同的整数，数字间以空格分隔，要求将之顺次插入一棵初始为空的二叉搜索树。之后给出一个正整数M（≤100），随后M行，每行给出一句待判断的陈述句。陈述句有以下6种：

  • A is the root，即"A是树的根"；
  • A and B are siblings，即"A和B是兄弟结点"；
  • A is the parent of B，即"A是B的双亲结点"；
  • A is the left child of B，即"A是B的左孩子"；
  • A is the right child of B，即"A是B的右孩子"；
  • A and B are on the same level，即"A和B在同一层上"。

题目保证所有给定的整数都在整型范围内。

输出格式：

对每句陈述，如果正确则输出Yes，否则输出No，每句占一行。

输入样例：

5
2 4 1 3 0
8
2 is the root
1 and 4 are siblings
3 and 0 are on the same level
2 is the parent of 4
3 is the left child of 4
1 is the right child of 2
4 and 0 are on the same level
100 is the right child of 3

输出样例：

Yes
Yes
Yes
Yes
Yes
No
No
No
#include <bits/stdc++.h>
using namespace std;
struct BTNode
{int data;	BTNode* left;BTNode* right;BTNode(int x):data(x),left(NULL),right(NULL){};
}*root;
int m,n,t,level[50000];      //全局变量
void CreateBSTree(BTNode*& root,int x)
{if(root == NULL)root = new BTNode(x);else if(root->data > x)CreateBSTree(root->left,x);else CreateBSTree(root->right,x);
}
void levelorder(BTNode* root)
{int front = 0,rear = 0;n = 1;BTNode* que[100000] = {};if(root)que[rear++] = root;while(front != rear && n <= 50000){BTNode* p = que[front++];if(p){level[n++] = p->data;que[rear++] = p->left;que[rear++] = p->right;}else{n++;rear += 2;}}
}
int height(BTNode* root,int x) //这里可以加上一句if(root == NULL)return 0;但我可以保证x一定存在于树中，所以不必判断
{if(root->data > x)return 1 + height(root->left,x);else if(root->data < x)return 1 + height(root->right,x);return 1;
}
void GetNum(char* str,int& a,int& b)
{int i = 0;   //这里去掉对a的负数判断后依然可以ac，所以去掉了a的符号判断while(str[i] != ' ')a = (a * 10 + str[i++] - '0');bool flag = 0;for(;str[i];i++){if(str[i] >= '0' && str[i] <= '9')b = (b * 10 + str[i] - '0');if(str[i] == '-')flag = 1;}if(flag)b = -b;
}
int find(int x)
{for(int i = 1;i <= n;i++)	if(level[i] == x)return i;return -INT_MAX;
}
int main()
{char str[100];for(int i = 0;i < 50000;i++)level[i] = -INT_MAX;cin >> n;for(int i = 0;i < n;i++){cin >> t;	CreateBSTree(root,t);}levelorder(root);cin >> m;getchar();for(int i = 0;i < m;i++){int a = 0,b = 0;cin.getline(str,100);GetNum(str,a,b);int fa = find(a),  fb = find(b);if(strstr(str,"root")){if(level[1] == a)cout << "Yes" << endl;else cout << "No" << endl;}else if(strstr(str,"siblings")){if(fa != -INT_MAX && fb != -INT_MAX && fa != fb && (fa / 2 == fb / 2))cout << "Yes" << endl;else cout << "No" << endl;}else if(strstr(str,"parent")){if(fa != -INT_MAX && fb != -INT_MAX && (fb / 2 == fa))cout << "Yes" << endl;else cout << "No" << endl;}else if(strstr(str,"left")){if(fa != -INT_MAX && fb != -INT_MAX && (fb * 2 == fa))cout << "Yes" << endl;else cout << "No" << endl;}else if(strstr(str,"right")){if(fa != -INT_MAX && fb != -INT_MAX && (fb * 2 + 1 == fa))cout << "Yes" << endl;else cout << "No" << endl;}else if(strstr(str,"same")){if(fa != -INT_MAX && fb != -INT_MAX && (height(root,a) == height(root,b)))cout << "Yes" << endl;else cout << "No" << endl;}}return 0;
}

 

 

这篇关于pta数据结构树和图实验题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/280483。

相关文章

Go语言中三种容器类型的数据结构详解

Go语言中三种容器类型的数据结构详解

《Go语言中三种容器类型的数据结构详解》在Go语言中,有三种主要的容器类型用于存储和操作集合数据：本文主要介绍三者的使用与区别,感兴趣的小伙伴可以跟随小编一起学习一下... 目录基本概念1. 数组（Array）2. 切片（Slice）3. 映射（Map）对比总结注意事项基本概念在 Go 语言中，有三种主要
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
PTA求一批整数中出现最多的个位数字

PTA求一批整数中出现最多的个位数字

作者 徐镜春 单位 浙江大学 给定一批整数，分析每个整数的每一位数字，求出现次数最多的个位数字。例如给定3个整数1234、2345、3456，其中出现最多次数的数字是3和4，均出现了3次。 输入格式： 输入在第1行中给出正整数N（≤1000），在第二行中给出N个不超过整型范围的非负整数，数字间以空格分隔。 输出格式： 在一行中按格式“M: n1 n2 ...”输出，其中M是最大次数，n
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

8.3 交换排序 8.3.1 冒泡排序 【算法特点】 (1) 稳定排序。 (2) 可用于链式存储结构。 (3) 移动记录次数较多，算法平均时间性能比直接插入排序差。当初始记录无序，n较大时， 此算法不宜采用。 #include <stdio.h>#include <stdlib.h>#define MAXSIZE 26typedef int KeyType;typedef char In
阅读更多...
STM32(十一)：ADC数模转换器实验

STM32(十一)：ADC数模转换器实验

AD单通道： 1.RCC开启GPIO和ADC时钟。配置ADCCLK分频器。 2.配置GPIO，把GPIO配置成模拟输入的模式。 3.配置多路开关，把左面通道接入到右面规则组列表里。 4.配置ADC转换器， 包括AD转换器和AD数据寄存器。单次转换，连续转换；扫描、非扫描；有几个通道，触发源是什么，数据对齐是左对齐还是右对齐。 5.ADC_CMD 开启ADC。 void RCC_AD
阅读更多...
HNU-2023电路与电子学-实验3

HNU-2023电路与电子学-实验3

写在前面： 一、实验目的 1.了解简易模型机的内部结构和工作原理。 2.分析模型机的功能，设计 8 重 3-1 多路复用器。 3.分析模型机的功能，设计 8 重 2-1 多路复用器。 4.分析模型机的工作原理，设计模型机控制信号产生逻辑。 二、实验内容 1.用 VERILOG 语言设计模型机的 8 重 3-1 多路复用器； 2.用 VERILOG 语言设计模型机的 8 重 2-1 多
阅读更多...
【408数据结构】散列 （哈希）知识点集合复习考点题目

【408数据结构】散列 （哈希）知识点集合复习考点题目

苏泽  “弃工从研”的路上很孤独，于是我记下了些许笔记相伴，希望能够帮助到大家    知识点 1. 散列查找 散列查找是一种高效的查找方法，它通过散列函数将关键字映射到数组的一个位置，从而实现快速查找。这种方法的时间复杂度平均为(
阅读更多...
浙大数据结构：树的定义与操作

浙大数据结构：树的定义与操作

四种遍历 #include<iostream>#include<queue>using namespace std;typedef struct treenode *BinTree;typedef BinTree position;typedef int ElementType;struct treenode{ElementType data;BinTree left;BinTre
阅读更多...
Python 内置的一些数据结构

Python 内置的一些数据结构

文章目录 1. 列表 (List)2. 元组 (Tuple)3. 字典 (Dictionary)4. 集合 (Set)5. 字符串 (String) Python 提供了几种内置的数据结构来存储和操作数据，每种都有其独特的特点和用途。下面是一些常用的数据结构及其简要说明： 1. 列表 (List) 列表是一种可变的有序集合，可以存放任意类型的数据。列表中的元素可以通过索
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2