第二十二章 染色法与匈牙利算法

一、使用场景——二分图

如下图所示，如果一个图中的点能够分成下图中的两个集合。集合中的点不相连，但是两个集合之间是由边连接的。那么这个图就是二分图。我们接下来介绍的染色法就是一种判断二分图的方法。

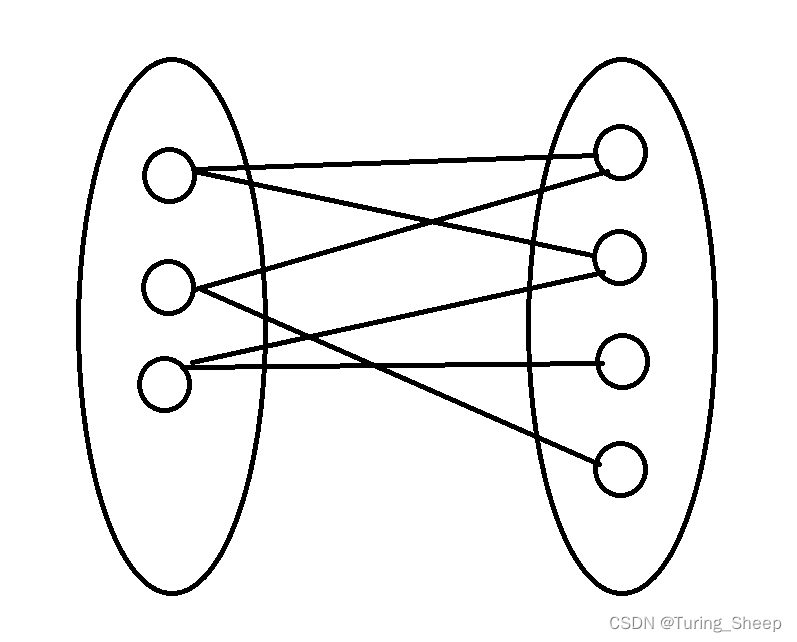
二、染色法

1、算法原理

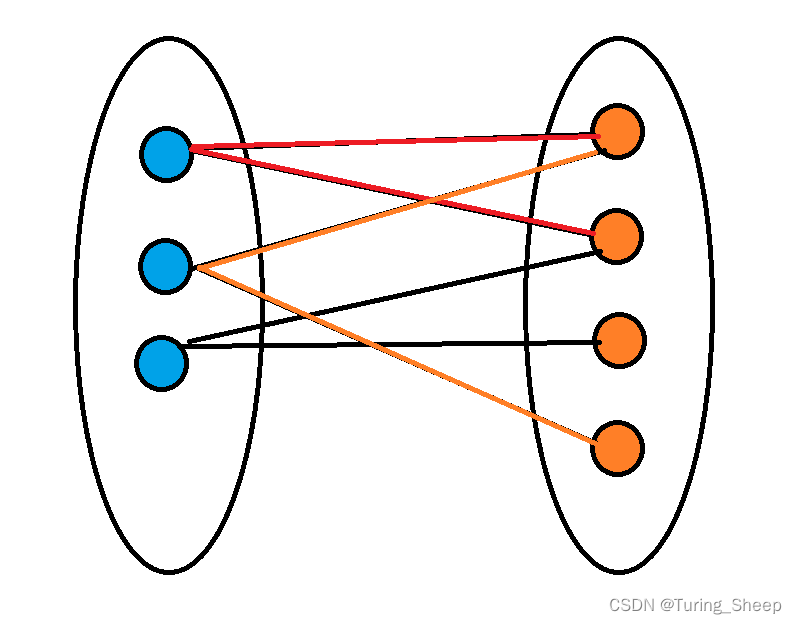
我们将左侧集合中的点染成蓝色，右边中的点染成橙色。我们会发现二分图的形成条件就是，图中所有点，父节点和该节点的颜色不同，该节点和子节点的颜色也不同。

我们可以用反证法：假设该节点和父节点颜色相同，但也是二分图。

由于二者的颜色相同，所以必定在同一个集合中。又因为二者是父子关系，所以二者之间一定是连了一条边，这就导致集合中的点之间出现了边，这和二分图的定义是矛盾的。

所以假设不成立，故我们的定理正确，即：图中的所有点，父节点和该节点的颜色不同，该节点和子节点的颜色也不同的时候，这个图就是二分图。

2、代码模板

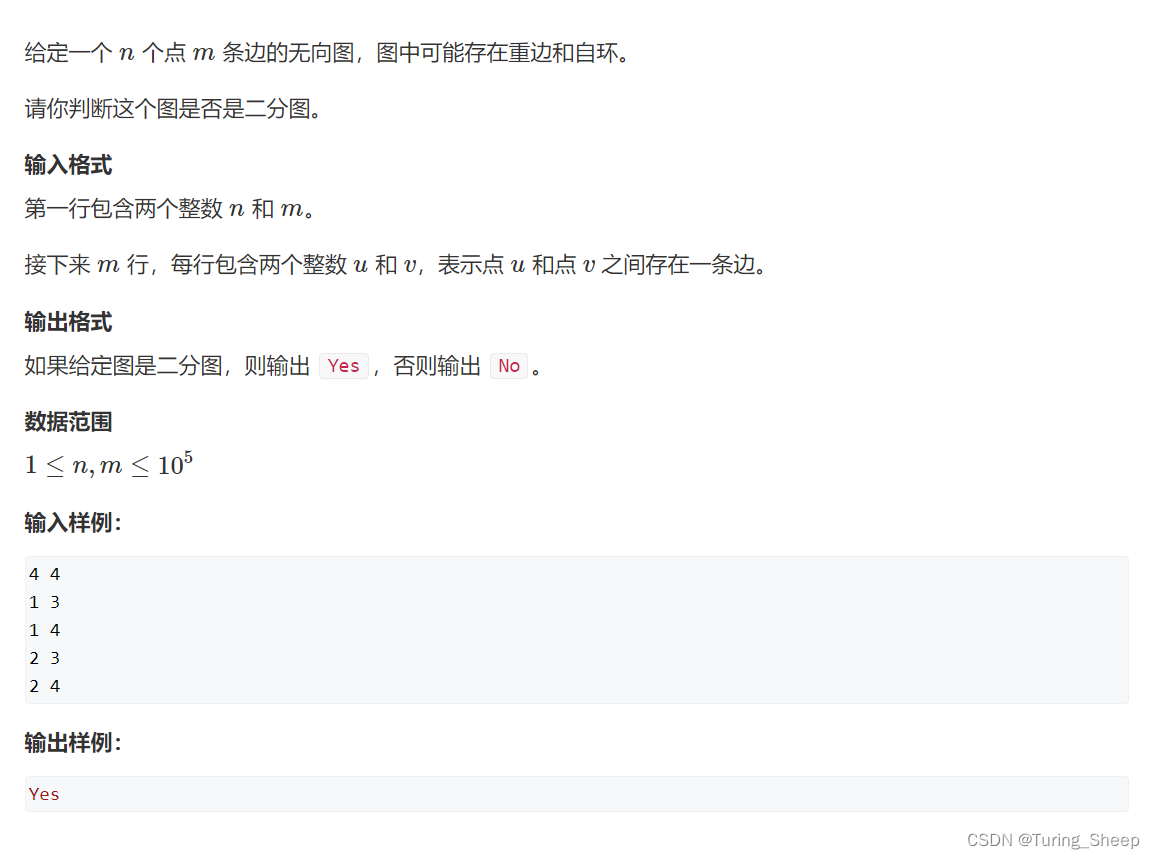
（1）问题：

（2）代码：

#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10,M=2*N;
int h[N],e[M],ne[M],idx,color[N];
int n,m;
void add(int x,int y)
{e[idx]=y,ne[idx]=h[x],h[x]=idx++;
}
bool dfs(int u,int x)
{color[u]=x;for(int i=h[u];i!=-1;i=ne[i]){if(!color[e[i]]){if(!dfs(e[i],3-x))return false;}else if(color[e[i]]==color[u])return false;}return true;
}
int main()
{memset(h,-1,sizeof h);cin>>n>>m;for(int i=0;i<m;i++){int a,b;scanf("%d%d",&a,&b);add(a,b),add(b,a);}bool flag=true;for(int i=1;i<=n;i++){if(!color[i]){if(!dfs(i,1)){flag=false;break;}}}if(flag)puts("Yes");else puts("No");return 0;
}

（3）分析：

我们这里解决一下主函数中为什么要去遍历一遍所有的点。其实这种做法就是为了避免非连通图的出现，例如下面的例子：

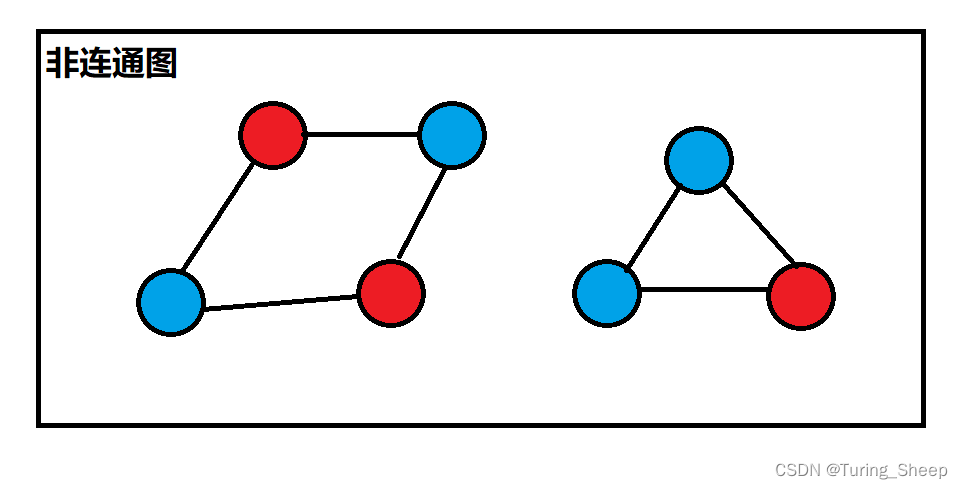
我们发现左侧的子图是二分图，但是右侧的子树不是二分图。而我们的dfs只能染色其中一个子图。因此，我们需要去遍历一遍所有的点，确定都是染了色的。

三、匈牙利算法

1、算法用途

我们先看下面这个图中的红色边：

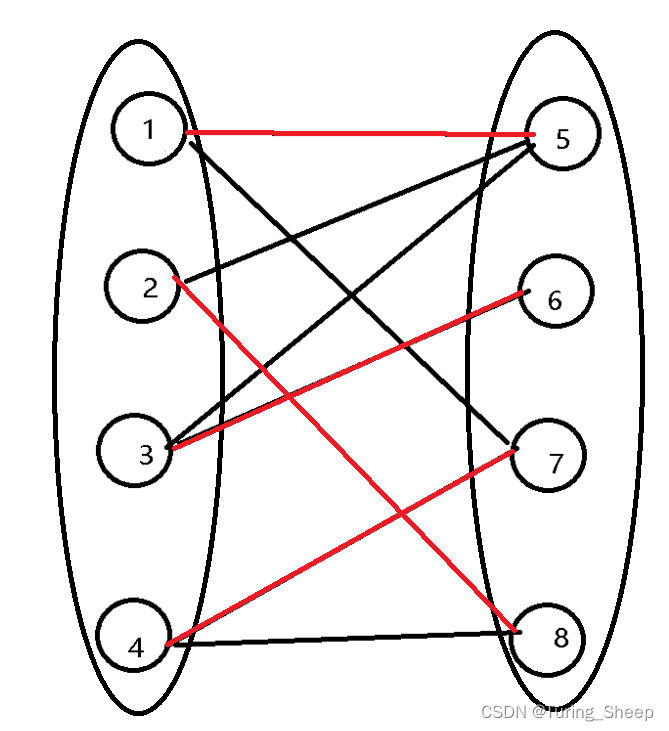
我们发现任何一个顶点只有一条红色边指向另一边。这种图唯一吗？答案是不唯一的。还有可能是下面这种结果：

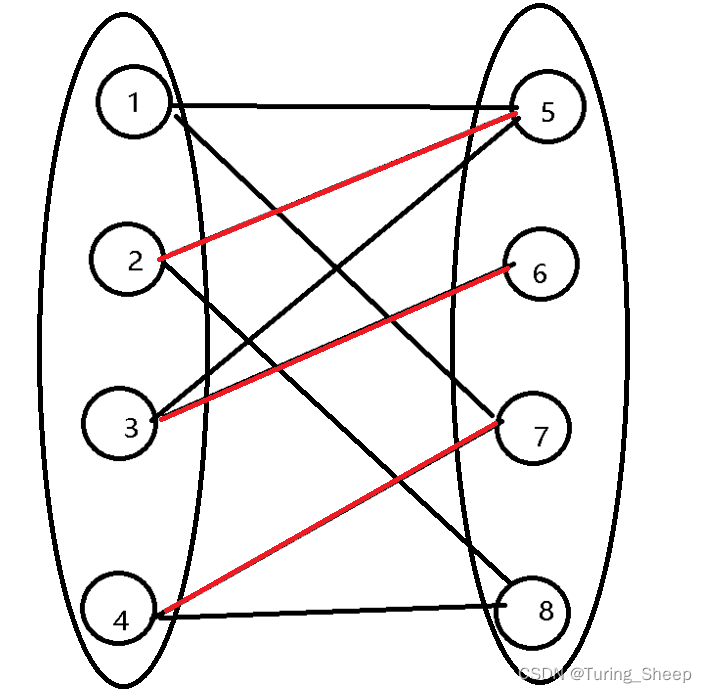
这也是一种连接方式。但是很明显第一种连接方式中红色边更多。那么这个红色边的数量是否存在一个最大值呢？我们接下来介绍的匈牙利算法就是解决这个问题的。

2、算法思路

这个算法的逻辑其实很简单，就是我们遍历左侧集合中的点A所对应的边W。如果边W对应的点B还没有红线连接，那么我就把A和B之间连上红线。如果边所对的右边集合中的点B已经被另外一个点C的红线连了。那么为了当前点A能够和点B之间搭上红线，我看看能不能让点C换一个，把B让给A。

其实就像，你追的人有对象了，那么我就看看能不能让你的情敌换一个对象，从而让你追到心上人。

3、算法模板

（1）问题

（2）代码

#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10,M=2e5+10;
int h[N],e[M],ne[M],idx;
int match[N];
bool st[N];
int n1,n2,m;
void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool find(int x)
{for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];if(!st[j]){st[j]=true;if(match[j]==0||find(match[j])){match[j]=x;return true;}}}return false;
}
int main()
{memset(h,-1,sizeof h);cin>>n1>>n2>>m;for(int i=0;i<m;i++){int a,b;scanf("%d%d",&a,&b);add(a,b);}int ans=0;for(int i=1;i<=n1;i++){memset(st,0,sizeof st);if(find(i))ans++;}cout<<ans<<endl;return 0;
}

（3）分析

st数组的解释：

st数组的作用是去标记每个点去寻找对象的时候，他们所考虑的人选。比如我想找A作为对象，那么我就把它标记为true，如果A已经有对象了，那我们让A的对象再去找一个，但是再去找的时候，你就别再找A了。因为A已经是我要考虑的了。