周长一定，问能组成多少种直角三角形（华为）

1. 题目

一个直角三角形的周长是120的话，那么它的三边可以是20，48，52，或者24，45，51，还有30，40，50，有3种不同的解。现在你想知道如果给定一个直角三角形的周长，那么这个周长最多能有多少解呢？假设边长为整数。

输入：120
输出：3

2.方案一：

解题思路：使用两次循环,指定i<=j,这样可以避免i与j重复枚举（例如345，435是同一个答案）来节约时间，k作为斜边，直接通过i、j 和周长便可以计算出k=len-i-j，减少一重循环。

注：

• 三角形的边长i，从1到给定周长的范围变化，即 1 <i< len
• 三角形的边长j，从i到给定周长的范围变化，即 i <j< len
• 三角形的边长k，k的长度为总长度减去i和j的长度，即k= len-i-j

public class FindNum1 {public static void findNum(int len){int count=0;for(int i=1;i<len;i++){for(int j=i;j<len;j++){int k=len-i-j;if(i*i+j*j==k*k){count++;}}}System.out.println(count);}public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int len=scanner.nextInt();findNum(len);}
}

方案二：

解题思路：我们对问题进行数学分析：

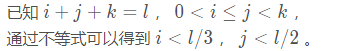
在二重循环的基础上，对i 和j 的范围进行限制,提高了查找效率。

public class FindNum2 {public static void findNum2(int len){int count=0;for(int i=1;i<len/3;i++){for(int j=i;j<len/2;j++){int k=len-i-j;if(i*i+j*j==k*k){count++;}}}System.out.println(count);}public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int len=scanner.nextInt();long start=System.currentTimeMillis();findNum2(len);long end=System.currentTimeMillis();System.out.println(end-start);}
}

方案三：

让我们重新回到数学上，2个方程2个未知数，我们可以轻松求出 j 关于i、l 的表达式。

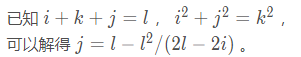
通过数学方法，我们获得了j的表达式，再判断一下j小于l并且j是整数便可。这样的程序只有一重循环了，我们将程序从一开始的超时优化到了1ms，这是枚举常见的优化方法——利用数学方法来减少循环次数。

public class FindNum3 {public static void findNum3(int len){int count=0;for(int i=1;i<len/3;i++){double j = len - (double) len * len/ (2 * len - 2 * i);if (i < j && j - (int) j < 1e-5) {count++;}}System.out.println(count);}public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int len=scanner.nextInt();findNum3(len);}
}

参考博客：https://blog.csdn.net/gooding300/article/details/86555475