本文主要是介绍【Joy of Cryptography 读书笔记】Chapter 3 秘密共享(Secret Sharing),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Chapter 3 秘密共享(Secret Sharing)
本章节介绍的是一项密码学技术:秘密共享。本章节首先介绍秘密共享的基本概念,然后介绍其基于多项式插值的Shamir实现。
文章目录
- Chapter 3 秘密共享(Secret Sharing)
- 一、基本概念
- 1、形式化定义
- 2、正确性
- 3、安全性
- 二、最简单的实现
- 三、多项式插值
- 1、实数上的多项式插值公式
- 2、扩展:模p
- 3、多项式的基数(#)
- 四、Shamir秘密共享
- 五*、视觉秘密共享
一、基本概念
1、形式化定义
定义3.1 一个( t , n t, n t,n)门限的秘密共享(t-out-of-n threshold secret-sharing scheme,TSSS)由以下算法构成:
- 秘密分发算法 S h a r e Share Share:一个随机算法,输入 m ∈ M m\in M m∈M,输出一系列秘密 s = ( s 1 , . . . s n ) s=(s_1,...s_n) s=(s1,...sn)
- 秘密重建算法 R e c o n s t r u c t Reconstruct Reconstruct:输入任意 t t t个秘密,就能重建输出 m m m
在秘密共享中,记 U ⊆ { 1 , . . . , n } U\subseteq\{1,...,n\} U⊆{1,...,n}是一个用户子集, { s i ∣ i ∈ U } \{s_i|i\in U\} {si∣i∈U}就是一组秘密分发。如果 ∣ U ∣ ≥ t |U|\ge t ∣U∣≥t,那么这组用户是授权的,也就是能够重建明文 m m m;否则是未授权的,不能知道明文的任何信息(部分信息也不可以)。
2、正确性
定义3.2 一个( t , n t, n t,n)门限的秘密共享是正确的,当且仅当对于所有授权的用户子集 U ⊆ { 1 , . . . , n } , ∣ U ∣ ≥ t U\subseteq\{1,...,n\},|U|\ge t U⊆{1,...,n},∣U∣≥t,以及对应的所有秘密分发 s ← S h a r e ( m ) s\leftarrow Share(m) s←Share(m),都有 R e c o n s t r u c t ( { s i ∣ i ∈ U } ) = m Reconstruct(\{s_i|i\in U\})=m Reconstruct({si∣i∈U})=m。
3、安全性
根据感性理解,秘密共享的安全性要求:对于未授权的用户将无法知道任何信息。下面给出形式化定义。
定义3.3 一个秘密共享算法 Σ \Sigma Σ是安全的,当且仅当 L t s s s − L Σ ≡ L t s s s − R Σ L_{tsss-L}^\Sigma \equiv L_{tsss-R}^\Sigma Ltsss−LΣ≡Ltsss−RΣ,其中库的定义如下:

注意:是同一组用户子集 U i U_i Ui
对定义3.3的理解:安全性的定义基本是按照第二章的“left vs right”。这里安全性更多的是关注未授权的情况下,无论明文是什么,秘密分发的结果的概率分布相同,那就没有泄露信息。至于授权的情况,就没有泄露一说,因此处理为err(不是说不执行算法,而是在安全性上不关心这种情况)。
二、最简单的实现
这里将介绍一个简单的(2,2)门限秘密共享(2-out-of-2 TSSS)的实现。它是两方的秘密共享,也是最简单的一个场景。具体算法如下:

它的正确性显而易见(因为上述两个算法和一次性密码本的加密、解密是相同的)。下面主要证明它的安全性(定义3.3),即证明 L t s s s − L Σ ≡ L t s s s − R Σ L_{tsss-L}^\Sigma \equiv L_{tsss-R}^\Sigma Ltsss−LΣ≡Ltsss−RΣ,这里也是使用了Hybrid方法:

第1步是对 ∣ U ∣ < 2 |U|<2 ∣U∣<2的情况进行展开,可以分为三种情况,然后思考如何转换为 L t s s s − R Σ L_{tsss-R}^\Sigma Ltsss−RΣ。然后首先看第一种情况,可以看到分发的秘密只有 s 1 s_1 s1, s 2 s_2 s2与分发结果无关,因此在第2步中可以将 m L m_L mL转换为 m R m_R mR。然后针对第二种情况,可以发现这个秘密的构建和一次性密码本的加密算法是一样的,因此相当于调用一次性密码本的算法 L o s t − L O T P L_{ost-L}^{OTP} Lost−LOTP,这就是第3步的转换。在第4步,由于在第一章已经证明过一次性密码本的安全性,即 L o s t − L O T P ≡ L o s t − R O T P L_{ost-L}^{OTP}\equiv L_{ost-R}^{OTP} Lost−LOTP≡Lost−ROTP,因此此处进行替换。第5步进行内联,发现这三种情况都已经是转化为使用 m R m_R mR了,因此第6步得到了 L t s s s − R Σ L_{tsss-R}^\Sigma Ltsss−RΣ。
可以看到,上述证明中使用到了一次性密码本的安全性。其实还有一个更一般性的结论:对于已经证明具有一次性安全性(定义2.6 one-time secrecy)的算法 Σ \Sigma Σ,那么如下的(2,2)门限秘密共享算法也是安全的:

三、多项式插值
在介绍秘密共享的进一步具体实现前,先介绍多项式插值的原理
1、实数上的多项式插值公式
定理3.1 对于一组确定的点集 { ( x 1 , y 1 ) , . . . , ( x d + 1 , y d + 1 ) } ⊆ R 2 \{(x_1,y_1), ...,(x_{d+1},y_{d+1})\}\subseteq R^2 {(x1,y1),...,(xd+1,yd+1)}⊆R2(其中 x i x_i xi均不相同),确定了唯一一个(至多) d d d次多项式 f f f,其系数都是实数且满足所有的点都在多项式上(即 y i = f ( x i ) , i = 1 , . . . , d + 1 y_i=f(x_i),i=1,...,d+1 yi=f(xi),i=1,...,d+1)。
**证明:**考虑如下的(至多) d d d次多项式(实际上它被称为拉格朗日多项式)
l j ( x ) = ( x − x 1 ) . . . ( x − x j − 1 ) ( x − x j + 1 ) . . . ( x − x d + 1 ) ( x j − x 1 ) . . . ( x j − x j − 1 ) ( x j − x j + 1 ) . . . ( x j − x d + 1 ) l_j(x)=\frac{(x-x_1)...(x-x_{j-1})(x-x_{j+1})...(x-x_{d+1})}{(x_j-x_1)...(x_j-x_{j-1})(x_j-x_{j+1})...(x_j-x_{d+1})} lj(x)=(xj−x1)...(xj−xj−1)(xj−xj+1)...(xj−xd+1)(x−x1)...(x−xj−1)(x−xj+1)...(x−xd+1)
可以知道它的取值为
l j ( x i ) = { 1 i = j 0 i ≠ j l_j(x_i)=\left\{ \begin{array}{rcl} 1 & i=j \\ 0 & i \neq j \end{array} \right. lj(xi)={10i=ji=j
因此,考虑如下多项式:
f ( x ) = y 1 l 1 ( x ) + y 2 l 2 ( x ) + . . . + y d + 1 l d + 1 ( x ) f(x)=y_1l_1(x)+y_2l_2(x)+...+y_{d+1}l_{d+1}(x) f(x)=y1l1(x)+y2l2(x)+...+yd+1ld+1(x)
可知 f ( x ) f(x) f(x)是一个(至多) d d d次多项式,而且对于每一个 x i x_i xi,都只有 l i ( x i ) = 1 l_i(x_i)=1 li(xi)=1,其余为 0 0 0,因此满足 f ( x i ) = y i f(x_i)=y_i f(xi)=yi。故 f ( x ) f(x) f(x)便是满足定理要求的一个多项式。
根据这个 f ( x ) f(x) f(x)的定义,可以知道求解 f ( 0 ) = ∑ i = 1 d + 1 y i ∏ j = 1 , . . . d + 1 , j ≠ i x j x j − x i f(0)=\sum_{i=1}^{d+1}y_i\prod_{j=1,...d+1,j\neq i}\frac{x_j}{x_j-x_i} f(0)=∑i=1d+1yi∏j=1,...d+1,j=ixj−xixj。
下面证明 f ( x ) f(x) f(x)的唯一性。假设还有一个 f ′ ( x ) f'(x) f′(x),构造 g ( x ) = f ( x ) − f ′ ( x ) g(x)=f(x)-f'(x) g(x)=f(x)−f′(x),可知 g ( x ) g(x) g(x)也是一个(至多) d d d次多项式,而且满足 g ( x i ) = 0 , i = 1 , . . . , d + 1 g(x_i)=0,i=1,...,d+1 g(xi)=0,i=1,...,d+1。这说明 g ( x ) g(x) g(x)有 d + 1 d+1 d+1个实根,但是最高次项至多 d d d次,因此 g ( x ) = 0 g(x)=0 g(x)=0,即 f ( x ) = f ′ ( x ) f(x)=f'(x) f(x)=f′(x),故证明了唯一性。
2、扩展:模p
定理3.2 对于质数 p p p 和一组确定的点集 { ( x 1 , y 1 ) , . . . , ( x d + 1 , y d + 1 ) } ⊆ Z p 2 \{(x_1,y_1), ...,(x_{d+1},y_{d+1})\}\subseteq Z_p^2 {(x1,y1),...,(xd+1,yd+1)}⊆Zp2(其中 x i x_i xi均不相同, Z p Z_p Zp是指小于 p p p的非负整数),确定了唯一一个(至多) d d d次多项式 f f f,其系数来自 Z p Z_p Zp且满足所有的点模 p p p后都在多项式上(即 y i ≡ p f ( x i ) , i = 1 , . . . , d + 1 y_i\equiv_pf(x_i),i=1,...,d+1 yi≡pf(xi),i=1,...,d+1)。
这个定理是对定理3.1的一个扩展,也就是模 p p p后依然成立。它的证明和定理3.1的证明几乎是一致的,只不过需要说明加、减、乘、除法模 p p p后能保证同余。加、减、乘法的结果是显然的;至于除法,在 p p p是质数的前提下是成立的,不再做过多的证明。
3、多项式的基数(#)
定理3.3 对于质数 p p p 和一组确定的点集 { ( x 1 , y 1 ) , . . . , ( x k , y k ) } ⊆ Z p 2 \{(x_1,y_1), ...,(x_{k},y_{k})\}\subseteq Z_p^2 {(x1,y1),...,(xk,yk)}⊆Zp2(其中 x i x_i xi均不相同),如果 d d d满足 k ≤ d k\le d k≤d且 p > d p>d p>d,那么满足系数来自 Z p Z_p Zp且穿过所有的点模 p p p后的值(即 y i ≡ p f ( x i ) , i = 1 , . . . , k y_i\equiv_pf(x_i),i=1,...,k yi≡pf(xi),i=1,...,k)的多项式的个数是 p d + 1 − k p^{d+1-k} pd+1−k。
**证明:**采用数学归纳法进行证明。首先如果 k = d + 1 k=d+1 k=d+1,那么根据定理3.2可以知道只有唯一一个多项式, p d + 1 − k = p 0 = 1 p^{d+1-k}=p^0=1 pd+1−k=p0=1,成立。
对于 k ≤ d k\le d k≤d,假设大于 k k k的情况下定理都成立(递归假设)。那么对于 k k k而言,取一个额外的点 x ∗ ∈ Z p , x ∗ ≠ x i , i = 1 , . . . , k x^*\in Z_p,x^*\neq x_i,i = 1,...,k x∗∈Zp,x∗=xi,i=1,...,k。那么对应的 y ∗ y^* y∗共有 ∣ Z p ∣ |Z_p| ∣Zp∣种取值。因此计算这 k k k个点确定的多项式的个数,相当于计算这 k k k个点再加上 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗)所确定的多项式的个数(因为都是 x ∗ x^* x∗,仅 y ∗ y^* y∗不同,因此每一组 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗)确定的多项式必不相同):
k 个点确定的多项式数量 = 等价转化 ∑ y ∗ ∈ Z p k 个点和 ( x ∗ , y ∗ ) 确定的多项式数量 = 递归假设 ∑ y ∗ ∈ Z p p d + 1 − ( k + 1 ) = ∣ Z p ∣ = p p ⋅ p d + 1 − ( k + 1 ) = p d + 1 − k \begin{aligned} k个点确定的多项式数量 \overset{等价转化}=& \sum_{y^* \in Z_p}k个点和(x^*,y^*)确定的多项式数量\\ \overset{递归假设}=& \sum_{y^* \in Z_p}p^{d+1-(k+1)}\\ \overset{|Z_p|=p}=& p\cdot p^{d+1-(k+1)}= p^{d+1-k}\\ \end{aligned} k个点确定的多项式数量=等价转化=递归假设=∣Zp∣=py∗∈Zp∑k个点和(x∗,y∗)确定的多项式数量y∗∈Zp∑pd+1−(k+1)p⋅pd+1−(k+1)=pd+1−k
由此得证。
四、Shamir秘密共享
基于多项式插值,Shamir实现了一种秘密共享的算法(SSS),具体算法如下:

在算法中,将秘密生成一个 t − 1 t-1 t−1次多项式,明文作为多项式的常数项。然后将一个点作为秘密分发给用户。根据多项式插值,至少 t t t个点就可以求解出该多项式,并计算 f ( 0 ) f(0) f(0)获取 m m m;少于 t t t个点则无法确定唯一的多项式,因此无法获取信息——这正实现了秘密共享。该算法的正确性可以由多项式插值定理保证。
下面证明该算法的安全性(定义3.3)。首先需要证明一个引理:如果未授权,那么每个用户获取的秘密(也就是 y i y_i yi)相当于随机(等概率)取点。其形式化表示如下。
引理:对于一个质数 p p p,如下定义的两个库等价,即 L s h a m i r − r e a l ≡ L s h a m i r − r a n d L_{shamir-real}\equiv L_{shamir-rand} Lshamir−real≡Lshamir−rand:

引理证明:对于给定的 m ∈ Z p , U ( ∣ U ∣ < t ) , y i m\in Z_p,U(|U|<t),y_i m∈Zp,U(∣U∣<t),yi,我们需要证明两个库给出对应结果的概率是相同的。
对于 L s h a m i r − r e a l L_{shamir-real} Lshamir−real,根据定理3.3可知,随机生成的不同多项式一共有 p t − 1 p^{t-1} pt−1个(因为只要求 f ( 0 ) = m f(0)=m f(0)=m,相当于只确定了一个点)。而通过 U U U重建所得的多项式,如果它也恰好满足 f ( 0 ) = m f(0)=m f(0)=m(称为“好多项式”),将有 p t − ∣ U ∣ − 1 p^{t-|U|-1} pt−∣U∣−1个(知道 ∣ U ∣ + 1 |U|+1 ∣U∣+1个点)。因此如果泄露秘密,那么随机生成的多项式应当是“好多项式”,其概率为 p t − ∣ U ∣ − 1 p t − 1 = p − ∣ U ∣ \frac{p^{t-|U|-1}}{p^{t-1}}=p^{-|U|} pt−1pt−∣U∣−1=p−∣U∣。
对于随机取点的 L s h a m i r − r a n d L_{shamir-rand} Lshamir−rand,每一个用户的 y i y_i yi都有 p p p种取值,故秘密 s s s一共有 p ∣ U ∣ p^{|U|} p∣U∣种。而对于一个多项式而言,不同的 x x x的取值必然只有一个,因此恰好取到这一种的概率为 p − ∣ U ∣ p^{-|U|} p−∣U∣。
因此两个库等价。
有了引理,接下来就可以使用Hybrid方法证明Shamir算法的安全性,也就是证明 L t s s s − L S ≡ L t s s s − R S L_{tsss-L}^S\equiv L_{tsss-R}^S Ltsss−LS≡Ltsss−RS。证明如下:
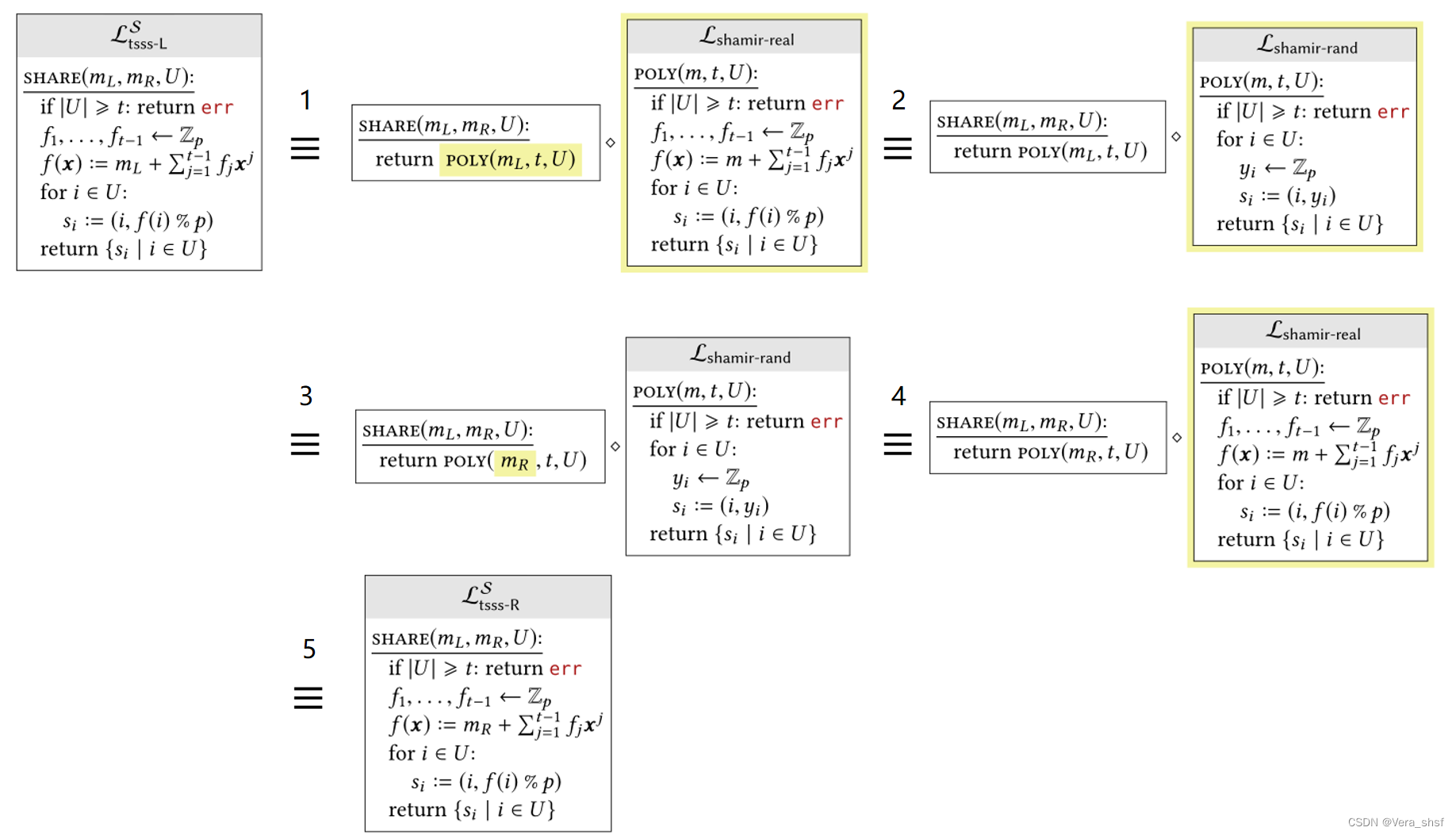
第1步时将其拆分为调用库 L s h a m i r − r e a l L_{shamir-real} Lshamir−real的形式,然后第2步根据引理将其等价替换为 L s h a m i r − r a n d L_{shamir-rand} Lshamir−rand。由于 L s h a m i r − r a n d L_{shamir-rand} Lshamir−rand中没有用到输入的 m L m_L mL,因此在第3步将其换为 m R m_R mR依然成立。第4步在此利用引理换回 L s h a m i r − r e a l L_{shamir-real} Lshamir−real,内联后得到 L t s s s − R S L_{tsss-R}^S Ltsss−RS。
五*、视觉秘密共享
对于一些视觉信息(比如图片),也可以有秘密共享的方案。下面给出的是一个简单秘密分发方案,它是对每一个1x1的像素块进行秘密分发,分为两个2x2的像素块。因此一个图片最终会秘密分发为两个图片,而这两个图片的叠加就可以还原原始图片。

这篇关于【Joy of Cryptography 读书笔记】Chapter 3 秘密共享(Secret Sharing)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





