Spartan: zkSNARKS without trusted setup 源代码解析

1. 引言

微软研究中心2020年论文《Spartan: Efficient and general-purpose zkSNARKs without trusted setup》，发表于Crypto 2020。

代码实现参见：

• https://github.com/microsoft/Spartan 【由Rust语言实现】

1.1 库依赖

https://github.com/microsoft/Spartan 中依赖的库有：

• curve25519-dalek：其中的features simd_backend表示引入了并行计算，运行效率最高。

curve25519-dalek = { version = "2", features = ["serde", "simd_backend"]}

• merlin：基于STROBE构建的transcript，实现了Fiat-Shamir transform，可将interactive protocol 转为non-interactive protocol。

• rand：可生成 random numbers，将这些 random numbers转换为 useful types and distributions，同时还提供 some randomness-related algorithms。

• digest：提供 cryptographic hash functions，又名 digest algorithms。

• sha3：提供 SHA-3 (Keccak) hash function。

• byteorder：encode/decode numbers in either big-endian or little-endian order。

• rayon：实现 data-parallelism。

• serde：实现 serialization/deserialization。

• bincode：A binary serialization / deserialization strategy that uses Serde for transforming structs into bytes and vice versa!

• subtle：实现了constant-time cryptographic implementations。

• rand_core：实现了：
  – base random number generator traits （rand库中也包含了。）
  – error-reporting types （rand库中也包含了。）
  – functionality to aid implementation of RNGs

• zeroize：Securely clear secrets from memory with a simple trait built on stable Rust primitives which guarantee memory is zeroed using an operation will not be ‘optimized away’ by the compiler.

• itertools：Extra iterator adaptors, iterator methods, free functions, and macros.

• colored： add colors in your terminal。

• flate2：压缩/解压缩。A streaming compression/decompression library DEFLATE-based streams in Rust.

• thiserror：provides a convenient derive macro for the standard library’s std::error::Error trait。

• criterion：Statistics-driven Microbenchmarking in Rust。It helps you write fast code by detecting and measuring performance improvements or regressions, even small ones, quickly and accurately。

1.2 基本结构

1.2.1 Spartan\src\error.rs：

枚举了一些错误类型。

1.2.2 Spartan\src\math.rs：

定义了基本的数学操作，如求平方根square_root、求二次幂pow2、求${\log }_2$ 值log2，以及获取数字二进制表示get_bits。

1.2.3 Spartan\src\timer.rs：

若配置了feature 为 profile，则提供计时开始new、停止stop、打印print的接口函数。

1.2.4 Spartan\src\scalar：

– ristretto255.rs：提供了 进位加法adc、借位减法sbb、求积后进位加法mac。定义了Scalar结构体，基于Scalar域内的各种运算。该部分代码主要来源于https://github.com/zkcrypto/bls12_381/blob/master/src/scalar.rs和https://github.com/zkcrypto/bls12_381/blob/main/src/util.rs。其中的invert和batch_invert函数来源于https://github.com/dalek-cryptography/curve25519-dalek/blob/master/src/ristretto.rs。
– mod.rs：将ristretto255.rs中定义的Scalar 结构体称为 Scalar，将curve25519_dalek::scalar:Scalar 称为 ScalarBytes。
定义了将usize或bool转换为Scalar的结构函数。以及将Scalar 转换为 ScalarBytes的相应的decompress函数。

1.2.5 Spartan\src\group.rs：

将curve25519_dalek::ristretto::RistrettoPoint 称为 GroupElement，将curve25519_dalek::ristretto::CompressedRistretto 称为 CompressedGroup。实现了scalar与groupelement的乘积运算，同时提供了vartime_multiscalar_mul。

1.2.6 Spartan\src\transcript.rs：

提供了ProofTranscript和AppendToTranscript trait，为 merlin::Transcript 提供了 append scalar或append compressedgroup的功能。同时提供生成challenge scalar(s)的接口函数。

1.2.7 Spartan\src\random.rs：

将merlin::Transcript封装为了RandomTape，提供了new、random_scalar和random_vector函数接口。

1.2.8 Spartan\src\nizk：

– bullet.rs：提供了inner_product函数，以及相应的Bulletproofs prove 和 verify 接口函数。该部分代码主要来源于https://github.com/dalek-cryptography/bulletproofs/。
– mod.rs：实现了Wahby等人2018年论文《Doubly-efficient zkSNARKs without trusted setup》中 “proof of knowledge of opening”、“proof of equality”、“proof of product”、“ZK vector dot-produt proof”、“proof of dot-product based on Bulletproofs” 。详见博客 Hyrax: Doubly-efficient zkSNARKs without trusted setup代码解析。

1.2.9 Spartan\src\commitments.rs：

MultiCommitGens 结构体中存储了commitment的GroupElement信息，适于vector commitment。

1.2.10 Spartan\src\dense_mlpoly.rs：

定义了multilinear polynomial。主要作用是将multilinear polynomial evaluation 转为 dot product （inner product）。

#[derive(Debug, Serialize, Deserialize)]
pub struct PolyCommitment {C: Vec<CompressedGroup>,
}pub struct DensePolynomial {num_vars: usize, // the number of variables in the multilinear polynomiallen: usize,Z: Vec<Scalar>, // evaluations of the polynomial in all the 2^num_vars Boolean inputs
}
impl PolyCommitmentGens {// the number of variables in the multilinear polynomialpub fn new(num_vars: usize, label: &'static [u8]) -> PolyCommitmentGens {let (_left, right) = EqPolynomial::compute_factored_lens(num_vars);let gens = DotProductProofGens::new(right.pow2(), label);PolyCommitmentGens { gens }}
}
//sum-check protocol中用于evaluate $\mathcal{G}$ at a random point in its domain $\vec{r}\in\mathbb{F}^{\mu}$。
pub struct EqPolynomial { r: Vec<Scalar>, //长度应与multilinear polynomial 变量个数相同。
}
pub struct PolyCommitmentGens { //generators：G_1,...,G_n,Hpub gens: DotProductProofGens,
}

博客 Spartan: zkSNARKS without trusted setup学习笔记 中第3节 “the sum-check protocol中 evaluate $\mathcal{G}$ at a random point in its domain $\vec{r}\in {\mathbb{F}}^{\mu }$” 的实际举例为：【实际即为对multilinear 多项式 valuate at random $\vec{r}\in {\mathbb{F}}^{\mu }$。】

#[test]fn check_polynomial_evaluation() {let mut Z: Vec<Scalar> = Vec::new(); // Z = [1, 2, 1, 4]Z.push(Scalar::one());Z.push((2 as usize).to_scalar());Z.push((1 as usize).to_scalar());Z.push((4 as usize).to_scalar());// r = [4,3]let mut r: Vec<Scalar> = Vec::new();r.push((4 as usize).to_scalar());r.push((3 as usize).to_scalar());// 拆分为 <(\vec{L}\cdot \mathbf{Z}), \vec{R}> 进行evaluation计算。let eval_with_LR = evaluate_with_LR(&Z, &r);let poly = DensePolynomial::new(Z);//直接对evaluate multilinear polynomial at $\vec{r}$。// 转换为 <\vec{chis}, \vec{Z}> 进行evaluation计算。let eval = poly.evaluate(&r); assert_eq!(eval, (28 as usize).to_scalar());assert_eq!(eval_with_LR, eval);}

multilinear polynomial commit：【针对有$m$个变量的multilinear polynomial，其$Z[x_1,\cdots ,x_m]$ for x i ∈ { 0 , 1 } x_i\in\{0,1\} xi​∈{0,1} 值有$n=2^m$个】

let (left_num_vars, right_num_vars) = EqPolynomial::compute_factored_lens(ell);
let L_size = left_num_vars.pow2();
let R_size = right_num_vars.pow2();
assert_eq!(L_size * R_size, n);// 将Z以矩阵形式表示，具有L_size行，R_size列，逐行进行commit。
let gens = PolyCommitmentGens::new(poly.get_num_vars(), b"test-two");
let (poly_commitment, blinds) = poly.commit(&gens, None); 

argument for multilinear polynomial evaluation证明：【核心思想为将evaluation 拆分为：$<(\vec{L}\cdot \mathbf{Z}),\vec{R}>=<\overrightarrow{LZ},\vec{R}>=eval$，其中$eval,\vec{R}$为public info，从而转为 inner product proof (dot product proof)，可直接使用博客 Hyrax: Doubly-efficient zkSNARKs without trusted setup代码解析
中的 “7. proof of dot-product based on Bulletproofs” 协议。】

 	let eval = poly.evaluate(&r);assert_eq!(eval, (28 as usize).to_scalar());let gens = PolyCommitmentGens::new(poly.get_num_vars(), b"test-two");let (poly_commitment, blinds) = poly.commit(&gens, None);let mut random_tape = RandomTape::new(b"proof");let mut prover_transcript = Transcript::new(b"example");let (proof, C_Zr) = PolyEvalProof::prove(&poly,Some(&blinds),&r,&eval,None,&gens,&mut prover_transcript,&mut random_tape,);let mut verifier_transcript = Transcript::new(b"example");assert!(proof.verify(&gens, &mut verifier_transcript, &r, &C_Zr, &poly_commitment).is_ok());}

1.2.11 Spartan\src\unipoly.rs：

定义了单变量多项式 以及 compressed单变量多项式。支持根据evaluation值恢复二阶或三阶多项式。【注释不准确。。。】

// cx^2 + bx + a stored as vec![a,b,c]
// dx^3 + cx^2 + bx + a stored as vec![a,b,c,d]
#[derive(Debug)]
pub struct UniPoly {coeffs: Vec<Scalar>,
}// cx^2 + bx + a stored as vec![a,c]
// dx^3 + cx^2 + bx + a stored as vec![a,c,d]
#[derive(Serialize, Deserialize, Debug)]
pub struct CompressedUniPoly {coeffs_except_linear_term: Vec<Scalar>,
}

单变量多项式 压缩为 compressed单变量多项式：

// cx^2 + bx + a stored as vec![a,c]
// dx^3 + cx^2 + bx + a stored as vec![a,c,d]
pub fn compress(&self) -> CompressedUniPoly {let coeffs_except_linear_term = [&self.coeffs[..1], &self.coeffs[2..]].concat();assert_eq!(coeffs_except_linear_term.len() + 1, self.coeffs.len());CompressedUniPoly {coeffs_except_linear_term,}}

compressed单变量多项式 解压缩为 单变量多项式：

  // we require eval(0) + eval(1) = hint, so we can solve for the linear term as:// linear_term = hint - 2 * constant_term - deg2 term - deg3 termpub fn decompress(&self, hint: &Scalar) -> UniPoly {let mut linear_term =hint - self.coeffs_except_linear_term[0] - self.coeffs_except_linear_term[0];for i in 1..self.coeffs_except_linear_term.len() {linear_term -= self.coeffs_except_linear_term[i];}let mut coeffs: Vec<Scalar> = Vec::new();coeffs.push(self.coeffs_except_linear_term[0]);coeffs.push(linear_term);coeffs.extend(&self.coeffs_except_linear_term[1..]);assert_eq!(self.coeffs_except_linear_term.len() + 1, coeffs.len());UniPoly { coeffs }}

相应的压缩/解压缩参见test 测试用例 test_from_evals_quad 和 test_from_evals_cubic：

  #[test]fn test_from_evals_quad() {// polynomial is 2x^2 + 3x + 1let e0 = Scalar::one();let e1 = (6 as usize).to_scalar();let e2 = (15 as usize).to_scalar();let evals = vec![e0, e1, e2];let poly = UniPoly::from_evals(&evals);assert_eq!(poly.eval_at_zero(), e0);assert_eq!(poly.eval_at_one(), e1);assert_eq!(poly.coeffs.len(), 3);assert_eq!(poly.coeffs[0], Scalar::one());assert_eq!(poly.coeffs[1], (3 as usize).to_scalar());assert_eq!(poly.coeffs[2], (2 as usize).to_scalar());let hint = e0 + e1;let compressed_poly = poly.compress();let decompressed_poly = compressed_poly.decompress(&hint);for i in 0..decompressed_poly.coeffs.len() {assert_eq!(decompressed_poly.coeffs[i], poly.coeffs[i]);}let e3 = (28 as usize).to_scalar();assert_eq!(poly.evaluate(&(3 as usize).to_scalar()), e3);}

1.2.12 Spartan\src\sumcheck.rs：

// 包含的证明函数有 prove_cubic、prove_cubic_batched
#[derive(Serialize, Deserialize, Debug)]
pub struct SumcheckInstanceProof {compressed_polys: Vec<CompressedUniPoly>,
}// 包含的证明函数有 prove_quad、prove_cubic_with_additive_term
#[derive(Serialize, Deserialize, Debug)]
pub struct ZKSumcheckInstanceProof {comm_polys: Vec<CompressedGroup>,comm_evals: Vec<CompressedGroup>,proofs: Vec<DotProductProof>,
}

1.2.13 Spartan\src\product_tree.rs：

#[derive(Debug)]
pub struct ProductCircuit {left_vec: Vec<DensePolynomial>,right_vec: Vec<DensePolynomial>,
}pub struct DotProductCircuit {left: DensePolynomial,right: DensePolynomial,weight: DensePolynomial,
}#[allow(dead_code)] //解决 “warning: code is never used”
#[derive(Debug, Serialize, Deserialize)]
pub struct LayerProof {pub proof: SumcheckInstanceProof,pub claims: Vec<Scalar>,
}
#[allow(dead_code)]
#[derive(Debug, Serialize, Deserialize)]
pub struct LayerProofBatched {pub proof: SumcheckInstanceProof,pub claims_prod_left: Vec<Scalar>,pub claims_prod_right: Vec<Scalar>,
}#[derive(Debug, Serialize, Deserialize)]
pub struct ProductCircuitEvalProof {proof: Vec<LayerProof>,
}
#[derive(Debug, Serialize, Deserialize)]
pub struct ProductCircuitEvalProofBatched {proof: Vec<LayerProofBatched>,claims_dotp: (Vec<Scalar>, Vec<Scalar>, Vec<Scalar>),
}

1.2.14 Spartan\src\sparse_mlpoly.rs：

// Scalar 矩阵描述
#[derive(Debug)]
pub struct SparseMatEntry {row: usize,col: usize,val: Scalar,
}// Polynomial 矩阵描述
#[derive(Debug)]
pub struct SparseMatPolynomial {num_vars_x: usize,num_vars_y: usize,M: Vec<SparseMatEntry>,
}
pub struct Derefs {row_ops_val: Vec<DensePolynomial>,col_ops_val: Vec<DensePolynomial>,comb: DensePolynomial,
}// polynomial commitment
#[derive(Debug, Serialize, Deserialize)]
pub struct DerefsCommitment {comm_ops_val: PolyCommitment,
}
#[derive(Debug, Serialize, Deserialize)]
pub struct PolyCommitment {C: Vec<CompressedGroup>,
}#[derive(Debug, Serialize, Deserialize)]
pub struct DerefsEvalProof {proof_derefs: PolyEvalProof,
}
#[derive(Debug, Serialize, Deserialize)]
pub struct PolyEvalProof {proof: DotProductProofLog,
}struct AddrTimestamps {ops_addr_usize: Vec<Vec<usize>>,ops_addr: Vec<DensePolynomial>,read_ts: Vec<DensePolynomial>,audit_ts: DensePolynomial,
}pub struct MultiSparseMatPolynomialAsDense {batch_size: usize,val: Vec<DensePolynomial>,row: AddrTimestamps,col: AddrTimestamps,comb_ops: DensePolynomial,comb_mem: DensePolynomial,
}pub struct SparseMatPolyCommitmentGens {gens_ops: PolyCommitmentGens,gens_mem: PolyCommitmentGens,gens_derefs: PolyCommitmentGens,
}#[derive(Debug, Serialize, Deserialize)]
pub struct SparseMatPolyCommitment {batch_size: usize,num_ops: usize,num_mem_cells: usize,comm_comb_ops: PolyCommitment,comm_comb_mem: PolyCommitment,
}#[derive(Debug)]
struct HashLayer {init: DensePolynomial,read_vec: Vec<DensePolynomial>,write_vec: Vec<DensePolynomial>,audit: DensePolynomial,
}#[derive(Debug)]
struct ProductLayer {init: ProductCircuit,read_vec: Vec<ProductCircuit>,write_vec: Vec<ProductCircuit>,audit: ProductCircuit,
}#[derive(Debug)]
struct Layers {hash_layer: HashLayer,prod_layer: ProductLayer,
}
#[derive(Debug)]
struct PolyEvalNetwork {row_layers: Layers,col_layers: Layers,
}
#[derive(Debug, Serialize, Deserialize)]
struct HashLayerProof {eval_row: (Vec<Scalar>, Vec<Scalar>, Scalar),eval_col: (Vec<Scalar>, Vec<Scalar>, Scalar),eval_val: Vec<Scalar>,eval_derefs: (Vec<Scalar>, Vec<Scalar>),proof_ops: PolyEvalProof,proof_mem: PolyEvalProof,proof_derefs: DerefsEvalProof,
}
#[derive(Debug, Serialize, Deserialize)]
struct ProductLayerProof {eval_row: (Scalar, Vec<Scalar>, Vec<Scalar>, Scalar),eval_col: (Scalar, Vec<Scalar>, Vec<Scalar>, Scalar),eval_val: (Vec<Scalar>, Vec<Scalar>),proof_mem: ProductCircuitEvalProofBatched,proof_ops: ProductCircuitEvalProofBatched,
}#[derive(Debug, Serialize, Deserialize)]
struct PolyEvalNetworkProof {proof_prod_layer: ProductLayerProof,proof_hash_layer: HashLayerProof,
}
#[derive(Debug, Serialize, Deserialize)]
pub struct SparseMatPolyEvalProof {comm_derefs: DerefsCommitment,poly_eval_network_proof: PolyEvalNetworkProof,
}pub struct SparsePolyEntry {idx: usize,val: Scalar,
}
pub struct SparsePolynomial {num_vars: usize,Z: Vec<SparsePolyEntry>,
}

相应的测试用例有：

  #[test]fn check_sparse_polyeval_proof() {let mut csprng: OsRng = OsRng;let num_nz_entries = 256;let num_rows = 256;let num_cols = 256;let num_vars_x = num_rows.log2();let num_vars_y = num_cols.log2();let mut M: Vec<SparseMatEntry> = Vec::new();for _i in 0..num_nz_entries {M.push(SparseMatEntry::new((csprng.next_u64() % (num_rows as u64)) as usize,(csprng.next_u64() % (num_cols as u64)) as usize,Scalar::random(&mut csprng),));}let poly_M = SparseMatPolynomial::new(num_vars_x, num_vars_y, M);let gens = SparseMatPolyCommitmentGens::new(b"gens_sparse_poly",num_vars_x,num_vars_y,num_nz_entries,3, //此处的batch_size为3，与下一行multi_commit函数参数&vec![&poly_M, &poly_M, &poly_M]的length为3对应。);// commitmentlet (poly_comm, dense) =SparseMatPolynomial::multi_commit(&vec![&poly_M, &poly_M, &poly_M], &gens);// evaluationlet rx: Vec<Scalar> = (0..num_vars_x).map(|_i| Scalar::random(&mut csprng)).collect::<Vec<Scalar>>();let ry: Vec<Scalar> = (0..num_vars_y).map(|_i| Scalar::random(&mut csprng)).collect::<Vec<Scalar>>();// 此处即为论文第7.1节公式（1）的$\bar{M}(\vec{r}_x)$值let eval = SparseMatPolynomial::multi_evaluate(&[&poly_M], &rx, &ry);let evals = vec![eval[0], eval[0], eval[0]];let mut random_tape = RandomTape::new(b"proof");let mut prover_transcript = Transcript::new(b"example");let proof = SparseMatPolyEvalProof::prove(&dense,&rx,&ry,&evals,&gens,&mut prover_transcript,&mut random_tape,);let mut verifier_transcript = Transcript::new(b"example");assert!(proof.verify(&poly_comm,&rx,&ry,&evals,&gens,&mut verifier_transcript,).is_ok());}

14.1) 论文7.2.1节中的Encoding sparse polynomials，对应为：

	// 对应表示的即为论文7.2.1节中的$\tilde{M}=\{i,j,M(i,j)\}_n$let mut M: Vec<SparseMatEntry> = Vec::new();for _i in 0..num_nz_entries { // 0~n-1M.push(SparseMatEntry::new((csprng.next_u64() % (num_rows as u64)) as usize,(csprng.next_u64() % (num_cols as u64)) as usize,Scalar::random(&mut csprng),));}

14.2）其中 struct AddrTimestamps 的作用为：
Encoding metadata for memory checking: “Memory in the head”：
有以下6种vectors的metadata：
1）$read-t{s}_{row}\in {\mathbb{F}}^n$ （表示read 操作对应的timestamp）
2）$write-t{s}_{row}\in {\mathbb{F}}^n$ （表示write 操作对应的timestamp）
3）$audit-t{s}_{row}\in {\mathbb{F}}^m$ （表示the final timestamps of memory cells in the offline memory checking primitive for the address sequence specified by $row$ over a memory of size $m=O(2^s)$。）
4）$read-t{s}_{col}\in {\mathbb{F}}^n$
5）$write-t{s}_{col}\in {\mathbb{F}}^n$
6）$audit-t{s}_{col}\in {\mathbb{F}}^m$
计算这些metadata仅需要如下参数：
（1）memory size (已由$2^s=m$确定)；
（2）the sequence of addresses at which the memory is accessed （由$row$和$col$提供）。
相应的rust伪代码示意为：

对应以上伪代码的实际代码实现为：

 pub fn new(num_cells: usize, num_ops: usize, ops_addr: Vec<Vec<usize>>) -> Self {for item in ops_addr.iter() {assert_eq!(item.len(), num_ops);}let mut audit_ts = vec![0usize; num_cells];let mut ops_addr_vec: Vec<DensePolynomial> = Vec::new();let mut read_ts_vec: Vec<DensePolynomial> = Vec::new();for ops_addr_inst in ops_addr.iter() {let mut read_ts = vec![0usize; num_ops];// since read timestamps are trustworthy, we can simply increment the r-ts to obtain a w-ts// this is sufficient to ensure that the write-set, consisting of (addr, val, ts) tuples, is a setfor i in 0..num_ops {let addr = ops_addr_inst[i];assert!(addr < num_cells);let r_ts = audit_ts[addr];read_ts[i] = r_ts;let w_ts = r_ts + 1;audit_ts[addr] = w_ts;}ops_addr_vec.push(DensePolynomial::from_usize(&ops_addr_inst));read_ts_vec.push(DensePolynomial::from_usize(&read_ts));}AddrTimestamps {ops_addr: ops_addr_vec,ops_addr_usize: ops_addr,read_ts: read_ts_vec,audit_ts: DensePolynomial::from_usize(&audit_ts),}}

14.3）论文7.2节的公式计算参见：

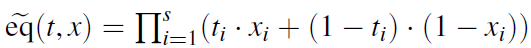
	// evaluationlet rx: Vec<Scalar> = (0..num_vars_x).map(|_i| Scalar::random(&mut csprng)).collect::<Vec<Scalar>>();let ry: Vec<Scalar> = (0..num_vars_y).map(|_i| Scalar::random(&mut csprng)).collect::<Vec<Scalar>>();let eval = SparseMatPolynomial::multi_evaluate(&[&poly_M], &rx, &ry);

  fn evaluate_with_tables(&self, eval_table_rx: &[Scalar], eval_table_ry: &[Scalar]) -> Scalar {assert_eq!(self.num_vars_x.pow2(), eval_table_rx.len());assert_eq!(self.num_vars_y.pow2(), eval_table_ry.len());(0..self.M.len()).map(|i| {let row = self.M[i].row;let col = self.M[i].col;let val = &self.M[i].val;eval_table_rx[row] * eval_table_ry[col] * val //？？好像与公式有点不一样？？}).sum()}pub fn multi_evaluate(polys: &[&SparseMatPolynomial],rx: &[Scalar],ry: &[Scalar],) -> Vec<Scalar> {let eval_table_rx = EqPolynomial::new(rx.to_vec()).evals();let eval_table_ry = EqPolynomial::new(ry.to_vec()).evals();(0..polys.len()).map(|i| polys[i].evaluate_with_tables(&eval_table_rx, &eval_table_ry)).collect::<Vec<Scalar>>()}

1.2.15 Spartan\src\lib.rs：

/// `SNARKGens` holds public parameters for producing and verifying proofs with the Spartan SNARK
pub struct SNARKGens {gens_r1cs_sat: R1CSGens,gens_r1cs_eval: R1CSCommitmentGens,
}/// Constructs a new `SNARKGens` given the size of the R1CS statementpub fn new(num_cons: usize, num_vars: usize, num_inputs: usize, num_nz_entries: usize) -> Self {let gens_r1cs_sat = R1CSGens::new(b"gens_r1cs_sat", num_cons, num_vars);let gens_r1cs_eval = R1CSCommitmentGens::new(b"gens_r1cs_eval",num_cons,num_vars,num_inputs, //public info 个数，通过1隔开，布局为[vars,1,io]num_nz_entries, //矩阵A/B/C中的非0元素个数。);SNARKGens {gens_r1cs_sat,gens_r1cs_eval,}}

pub struct R1CSGens {gens_sc: R1CSSumcheckGens,gens_pc: PolyCommitmentGens,
}pub fn new(label: &'static [u8], _num_cons: usize, num_vars: usize) -> Self {let num_poly_vars = num_vars.log2();let gens_pc = PolyCommitmentGens::new(num_poly_vars, label);let gens_sc = R1CSSumcheckGens::new(label, &gens_pc.gens.gens_1);R1CSGens { gens_sc, gens_pc }}

pub struct R1CSCommitmentGens {gens: SparseMatPolyCommitmentGens,
}
pub fn new(label: &'static [u8],num_cons: usize,num_vars: usize,num_inputs: usize,num_nz_entries: usize,) -> R1CSCommitmentGens {assert!(num_inputs < num_vars);let num_poly_vars_x = num_cons.log2();let num_poly_vars_y = (2 * num_vars).log2();let gens =SparseMatPolyCommitmentGens::new(label, num_poly_vars_x, num_poly_vars_y, num_nz_entries, 3);R1CSCommitmentGens { gens }}

pub struct SparseMatPolyCommitmentGens {gens_ops: PolyCommitmentGens,gens_mem: PolyCommitmentGens,gens_derefs: PolyCommitmentGens,
}
pub fn new(label: &'static [u8],num_vars_x: usize,num_vars_y: usize,num_nz_entries: usize,batch_size: usize,) -> SparseMatPolyCommitmentGens {let num_vars_ops =num_nz_entries.next_power_of_two().log2() + (batch_size * 5).next_power_of_two().log2();let num_vars_mem = if num_vars_x > num_vars_y {num_vars_x} else {num_vars_y} + 1;let num_vars_derefs =num_nz_entries.next_power_of_two().log2() + (batch_size * 2).next_power_of_two().log2();let gens_ops = PolyCommitmentGens::new(num_vars_ops, label);let gens_mem = PolyCommitmentGens::new(num_vars_mem, label);let gens_derefs = PolyCommitmentGens::new(num_vars_derefs, label);SparseMatPolyCommitmentGens {gens_ops,gens_mem,gens_derefs,}}

pub struct PolyCommitmentGens {pub gens: DotProductProofGens,
}// the number of variables in the multilinear polynomialpub fn new(num_vars: usize, label: &'static [u8]) -> PolyCommitmentGens {let (_left, right) = EqPolynomial::compute_factored_lens(num_vars);let gens = DotProductProofGens::new(right.pow2(), label);PolyCommitmentGens { gens }}
pub fn compute_factored_lens(ell: usize) -> (usize, usize) {(ell / 2, ell - ell / 2)}

pub struct DotProductProofGens {n: usize,pub gens_n: MultiCommitGens,pub gens_1: MultiCommitGens,
}
pub fn new(n: usize, label: &[u8]) -> Self {let (gens_n, gens_1) = MultiCommitGens::new(n + 1, label).split_at(n);DotProductProofGens { n, gens_n, gens_1 }}