二元阵常规波束图与其指向性—麦克风阵列系列（七）

本文主要是介绍二元阵常规波束图与其指向性—麦克风阵列系列（七），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

阅读原文还请移步我的知乎专栏：
https://www.zhihu.com/column/c_1287066237843951616

本篇包括内容为：

二元阵简介

例3.8 二元阵常规波束图

例3.9 二元阵指向性指数

二元阵简介

图1 二元阵

二元阵，即由两个阵元组成的阵列。将第一个阵元放置在坐标原点，第二个阵元放置在 $z$ 轴上，两阵元间距为 $d$ ，二元阵坐标系统如图1所示。两元阵的位置坐标为：

$\bold p _m=\left[ 0,0,(m-1)d \right]^T,m=1,2$

由于对称性，基阵方向性与水平方位角无关，只和俯仰角 $\phi$ 有关。因此该均匀线列阵的阵列流行向量为：

$\bold p(\phi)=\left[ 1,e^{kdcos\phi} \right]^T$

对于该二元阵，假设期望方向为 $\phi_o$ ，则加权向量为：

$\bold w^*\left( \phi_o \right)=\bold p^*\left( \phi_o \right)/2=\left[ 1,e^{-ikdcos\phi_o} \right]^T/2$

例3.8 二元阵常规波束图

该例考察阵元间距取不同值时二元阵常规波束响应。

假设阵元间距分别取 $d=0.05\lambda,0.25\lambda,0.5\lambda,$ 波束期望方向分别取 $\phi_o=0^\circ,60^\circ,90^\circ$ ，计算得到的常规波束图如图 $2(a),2(b),2(c)$ 显示。由图可见，当阵元间距逐渐减小时，二元阵的波束主瓣逐渐变宽，指向性逐渐变差。当阵元间距减小到 $d=0.05\lambda$ 时，二元阵的常规波束图接近于圆，即退化成了单个阵元，没有指向性。观察图2(a)发现，当 $d=0.25\lambda$ 时，波束图是一个倒“心形”，此时波束加权向量为：

$\bold w^*=\left[ \frac{1}{2}, -\frac{i}{2} \right]^T$

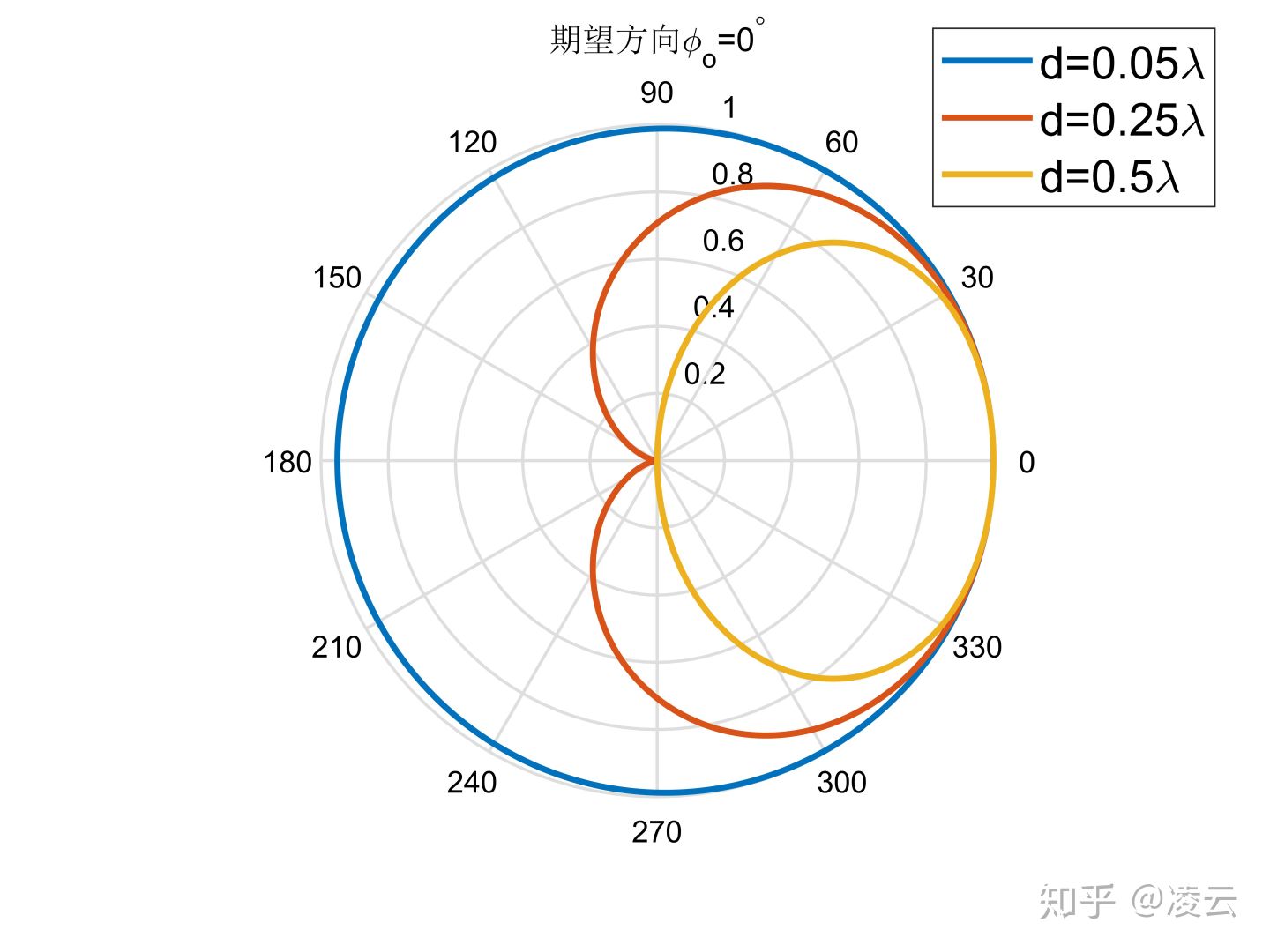
图 2(a)

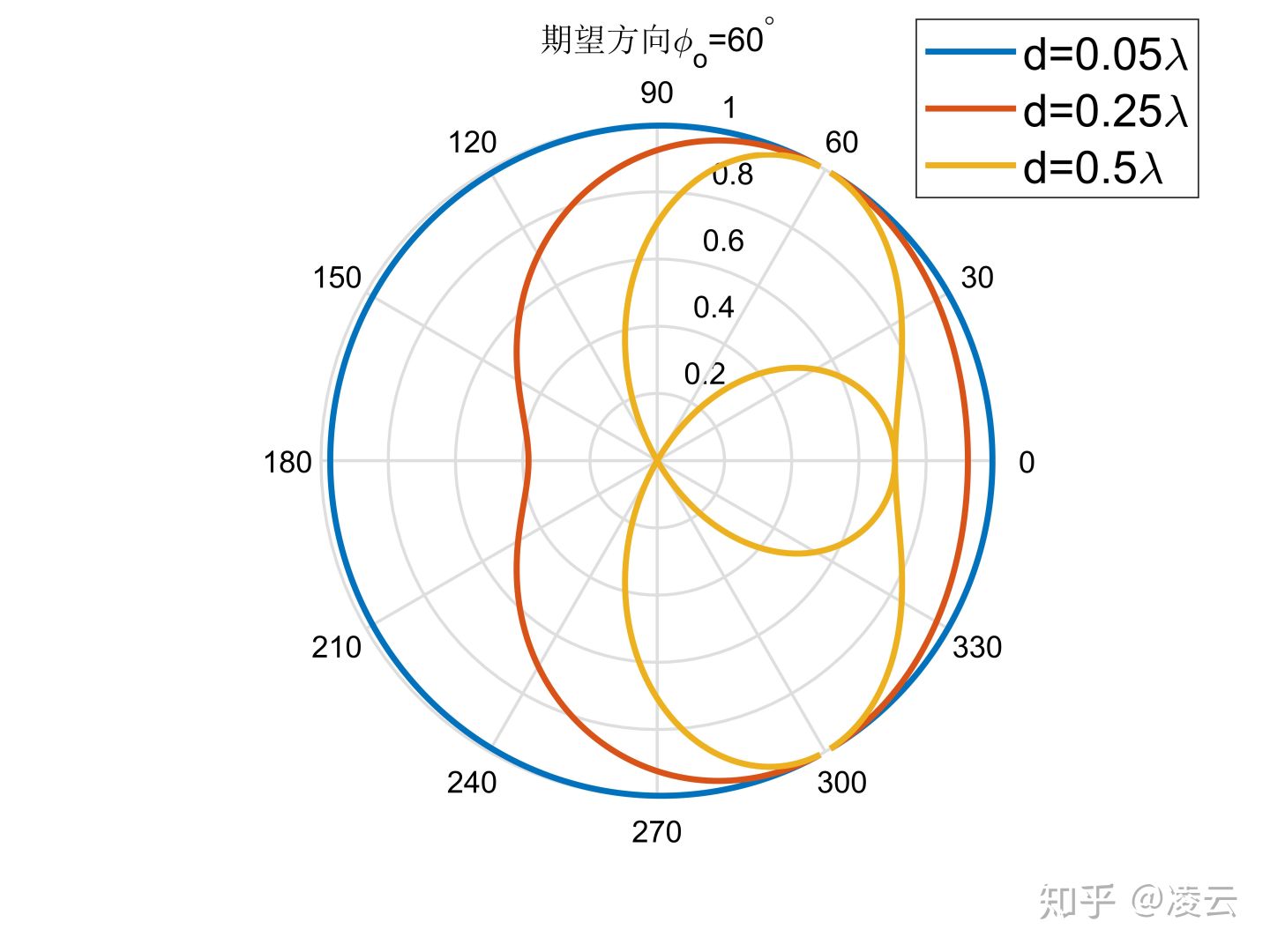
图 2(b)

图 2(c)

实现代码如下：

f=1000;      %频率
c=340;       %声速
lambda = c/f;
space=0.04;  %麦克风间距
theta_angle=0:1:360;
theta=theta_angle*pi/180;
space_list = [0.05 0.25 0.5]*lambda;  %连续阵间距
M = 2;
figure;
theta_d = 0 *pi/180;
for i = 1:length(space_list)space = space_list(i);B=sin((M*pi*f*space*(cos(theta)-cos(theta_d)))/c)..../(M*sin((pi*f*space*(cos(theta)-cos(theta_d)))/c));B_db=20*log10(B);index = B_db < -50;B_db(index) = -50;    GraphicHandle = polar(theta,B);set( GraphicHandle, 'LineWidth', 2);hold on;
end
title('期望方向\phi_o=0^\circ');
legend('d=0.05\lambda', 'd=0.25\lambda', 'd=0.5\lambda', 'fontsize', 15);

例3.9 二元阵指向性指数

基阵的指向性指数 基阵的指向性指数等于基阵在空间均匀各向同性噪声场中的阵增益。
超指向性 随着阵元间距的减小，线阵最佳波束形成形成在端射方向的指向性超过阵元个数，这种现状即为“超指向性”或“超增益”。

该例考虑一个二元阵，分别采用常规波束形成方法与最佳波束形成方法，考察不同阵元间距波长比 $\left( d/\lambda \right)$ 与不同观察方向情况下基阵的指向性指数。

假设波束观察方向分别为 $\phi_o=0^\circ,30^\circ,60^\circ,90^\circ,$ 让 $d/\lambda$ 在 $0\sim 0.5$ 范围内变化，分别利用下式（3.54)与式（3.56)

常规波束形成在二元阵在空间均匀各向同性噪声场中的阵增益为：

$Gain_c=\frac{\left| p^Hp \right|^2}{p\rho _{niso}p}=\frac{2}{1+sinc(kd)cos(kdcos\phi)}$

其中 $\rho_{niso}$ 为二元阵空间均匀各向同性噪声互谱矩阵：

$\rho_{niso}=\begin{gathered} \begin{bmatrix} 1 & sinc(kd) \\ sinc(kd) & 1 \end{bmatrix} \quad \end{gathered}$

最佳波束形成在二元阵在空间均匀各向同性噪声场中的阵增益为：

$Gain_{opt}=p^H\rho ^{-1}_{niso}p=\frac{2-2sinc(kd)cos(kdcos\phi)}{1-sinc^2(kd)}$

计算采用常规波束形成方法与最佳波束形成方法得到的指向性指数。两种波束形成方法的指向性计算结果分别显示于图3(a)与3(b)中。

图 3(a)

从图3(a)可以看出，对于常规波束形成方法，当 $d/\lambda =0.5$ 时，指向性 $Gain_c=2$ ，即阵元个数。波束观察方向为正横方向时（ $\phi_o=90^\circ$ )，随着 $d/\lambda$ 的减小，波束指向性逐渐减小，在 $d/\lambda$ 趋近于0时等于1，即没有指向性，等效于单个阵元。

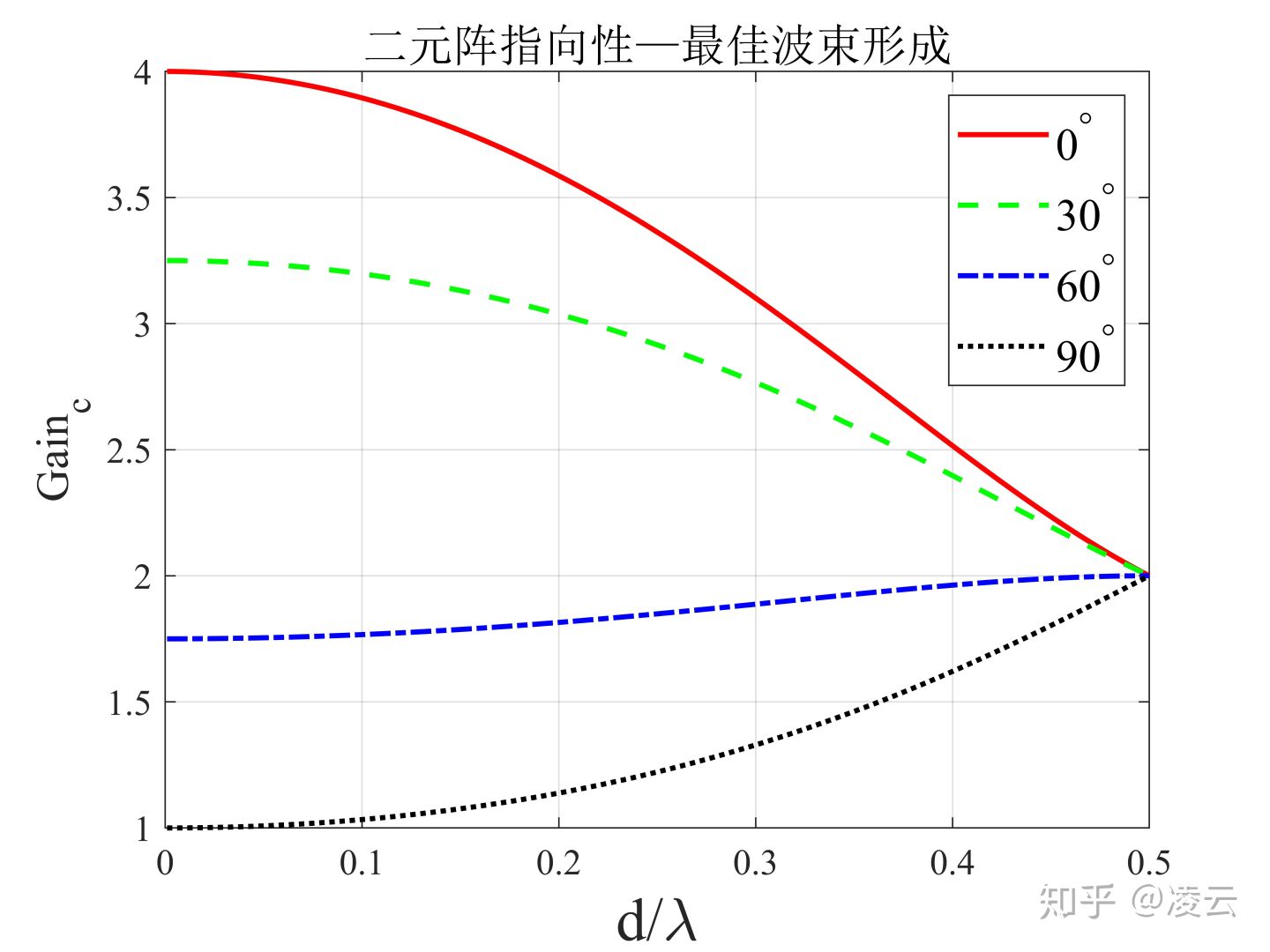
图 3(b)

观察图3(b)可以发现，采用最佳波束形成时，当波束观察方向为正横方向( $\phi_o=90^\circ$ )时，随着 $d/\lambda$ 从0.5逐渐减小到0，指向性从2逐渐减小到1。当波束观察方向为端射方向（ $\phi_o=0^\circ$ ）时，随着 $d/\lambda$ 从0.5逐渐减小到0，指向性从2逐渐增加到4，即为超指向性。

实现代码如下：

c = 340;
f = 1000;
lambda = c / f;
k = 2*pi*f/c; %波数
theta_angle=0:1:360;
theta=theta_angle*pi/180;
ratio_space = linspace(0.001, 0.5, 100);
space_list = ratio_space*lambda;  %连续阵间距
theta_d = [0 30 60 90] *pi/180;
color_list = {'r-' 'g--' 'b-.' 'k:'};
M = 2;
% 常规波束形成
figure;
for i = 1:length(theta_d)color = color_list{i};theta =  theta_d(i);Sinc = sin(k*space_list) ./ (k*space_list);Gain = 2 ./ (1+Sinc .* cos(k*space_list*cos(theta)));plot(ratio_space, Gain, color, 'linewidth', 1.5);hold on;
end
grid on;
xlabel('d/\lambda'); ylabel('Gain_c');
legend('0度', '30度', '60度', '90度', 'fontsize', 15);
title('二元阵指向性—常规波束形成');
% 最佳波束形成
figure;
for i = 1:length(theta_d)theta =  theta_d(i);color = color_list{i};Sinc = sin(k*space_list) ./ (k*space_list);Gain = (2 - 2*Sinc.*cos(k*space_list*cos(theta)))..../ (1-Sinc.^2);plot(ratio_space, Gain, color, 'linewidth', 1.5);hold on;
end
grid on;
xlabel('d/\lambda'); ylabel('Gain_{opt}');
legend('0度', '30度', '60度', '90度', 'fontsize', 15);
title('二元阵指向性—最佳波束形成');

参考书籍：

《优化阵列信号处理》

这篇关于二元阵常规波束图与其指向性—麦克风阵列系列（七）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！