（树形dp）hdu 3586 Information Disturbing

本文主要是介绍（树形dp）hdu 3586 Information Disturbing，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目
hdu3586

题意：
给出一个以结点1为根的树，切掉每一条边都有对应的代价，可以切掉任意条边，使得结点1到达不了这棵树所有的叶子结点，输出不超过代价m 的情况下的边的代价的最大值最小。

举个例子：在m = 5 的条件下：
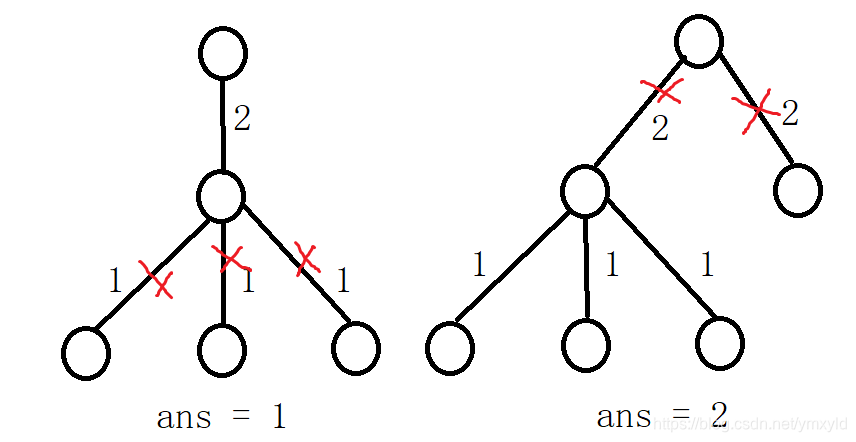
在这里插入图片描述
思路：
结点1到达不了这棵树所有的叶子结点可以转化为 $\sum$ 结点p 的下一层的子结点到达不了以子结点为根的子树所有的叶子结点的最小代价
但是题目求的是不超过代价m 的情况下的边的代价的最大值最小，如果用上面的思路可能答案有些错，就像上个例子的第二种情况一样，所有要枚举不超过代价1，2，3，，，m 的情况下，但是如果是从1 → m 枚举的话会TLE，那么就用二分来枚举。

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector> 
#define DEBUG freopen("_in.txt", "r", stdin); freopen("_out1.txt", "w", stdout);
using namespace std;
const int MAXN = 1e3 + 10;
const int INF = 1e6 + 10;
bool vis[MAXN];
int tree[MAXN], ti;
struct node{int v, w, next;
}R[MAXN<<1];
void addroad(int u, int v, int w){R[ti].v = v;R[ti].w = w;R[ti].next = tree[u];tree[u] = ti++;R[ti].v = u;R[ti].w = w;R[ti].next = tree[v];tree[v] = ti++;
}
int dfs(int p, int Max){vis[p] = true;int cnt = 0;for (int i = tree[p], s, w, sw; i != -1; i = R[i].next){s = R[i].v;w = R[i].w;if (!vis[s]){sw = dfs(s, Max);cnt += (w < sw && w <= Max) ? w : sw;}}return (cnt == 0) ? INF : cnt;  //这里巨坑，如果INF稍微大的一点点那么会反会一个负值。。。可以用一个数组来记录这个结点是否为叶子结点可以有效消除这种bug
}
int main(){int n, m;while (~scanf("%d%d", &n, &m) && !(n == 0 && m == 0)){memset(tree, -1, sizeof(tree));ti = 0;for (int i = 1, p, s, w; i < n; i++){scanf("%d%d%d", &p, &s, &w);addroad(p, s, w);}if (n == 1){printf("0\n");continue;}int l = 0, r = 1000, mid;memset(vis, false, sizeof(vis));if (dfs(1, r) > m){printf("-1\n");continue;}while (l < r){mid = (l + r) >> 1;memset(vis, false, sizeof(vis));if (dfs(1, mid) <= m)r = mid;elsel = mid + 1;}printf("%d\n", l);}return 0;
}