本文主要是介绍【路径追踪】前置知识1--辐射度测量学 Radiometry，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Intro
什么是辐射度测量学? 为什么需要辐射度测量学?
辐射度测量学为我们提供了用于描述光线传播和反射的相关概念以及数学工具.
图形学早期, 在各种条件的制约下, 我们一般通过诸如 Lambert 漫反射模型、Blinn-Phong 高光模型等计算表面光照. 这些经验模型能在一定程度上满足了人们对效率和效果的需求, 但是与产生令人信服的真实感渲染结果依旧存在较大的差距.
辐射度测量学就是用来解决这一问题的工具. 辐射度测量学通过精准表达光学的物理信息, 让我们得以在物理正确的基础上进行与光照相关的计算, 从而得到物理正确的结果.
光线追踪系统中对辐射度测量学的基本假设
虽然辐射度测量学是物理正确的, 但对于图形学来说, 我们只在集合光学领域进行计算. 在相关的讨论中都隐含着如下假设:
- 线性 Linearity: 光学系统中两个输入的合成效果通常等价于各自输入之和. 这一特性十分重要, 线性可加性极大的简化了我们对光线传输的分析与计算
- 能量守恒 Energy conservation
- 忽略偏振现象 No polarization
- 忽略荧光或磷光现象 No fluorescence or Phosphorescence
- 稳态 Steady state: 假设光线在环境中已经达到了稳定的状态, 所以 radiance 的分布不会随着时间的变化而变化. (在现实中光线的稳态往往在瞬间完成, 所以这一假设并不是系统产生的限制条件)
PS: 在这些条件下, 依旧难以有效表示的现象是光线的干涉和衍射现象. 产生这些现象的时候, 两片区域的全部 FLux 并不等于各自区域 Flux 的和.
辐射度测量学中的关键物理量
1. Radiant Energy
2. Flux(Power)
3. Intensity
4. Irradiance
5. Radiance
Radiant Energy
能量是辐射度测量学的起点, 单位是焦耳. 由于能量会随着时间不断累积, 所以在图形学领域很少使用能量进行研究, 但是我们需要使用的物理量都是由能量开始不断计算得出的.
Flux(Power)
Flux表示单位时间内辐射出的能量, Flux也被称为功率(Power).
在渲染时, 我们一般用 Flux 来表示光源的总发射量. 以点光源为例, 我们通过设置包围点光源的球壳来分析 Flux. 需要注意的是, 虽然大球壳上通过任何一个微面元的能量都小于小球壳上的, 但是由于大球壳同时拥有更大的表面积, 所以大小两个球壳上的总 Flux 是相等的.
衡量光源信息的重要物理量
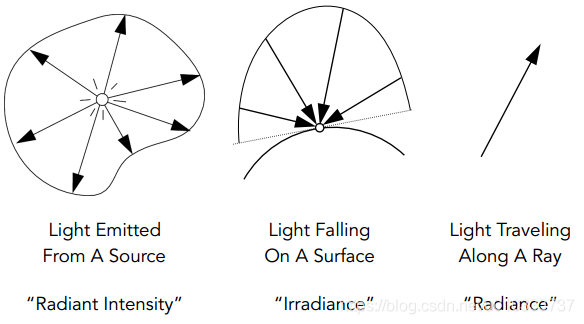
- Intensity : 定义光源辐射出多少能量
- Irradiance : 定义物体表面可以接收到多少能量
- Radiance : 定义光线在传播时的能量
Intensity
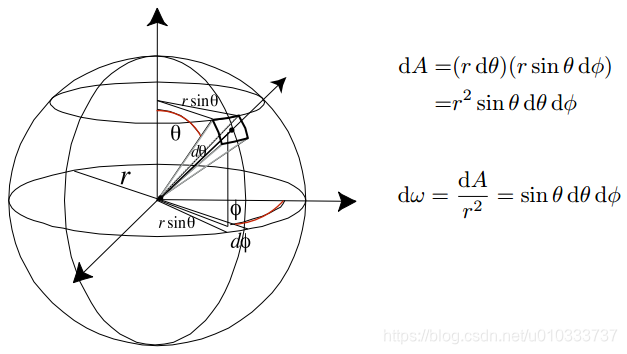
Intensity 表示单位立体角(Solid Angle)上光源辐射的 power.
那么什么是立体角? 我们知道平面上的一个角等于其对应的弧长除以半径. 立体角也采用非常类似的定义方式, 我们从球心发射一个类锥体会在球面上截取出一个面积, 立体角就等于这个面积除以半径的平方(注意! 我们所说的面积是在球面上的投影面积).
下图展示了微分立体角, 计算非常直观不再赘述.
Irradiance
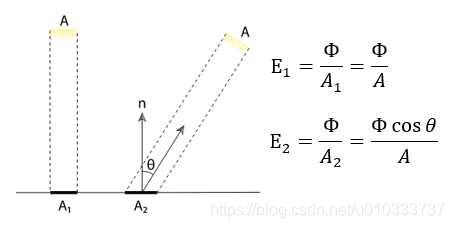
Irradiance 表示物体表面上单位面积上接收到的 power.
如下图所示, Irradiance 的定义同时也解释了 Lambert Cosine Law 的含义.
(Lambert Cosine Law : 到达物体表面的光能与光线方向和表面法线夹角的余弦成正比)
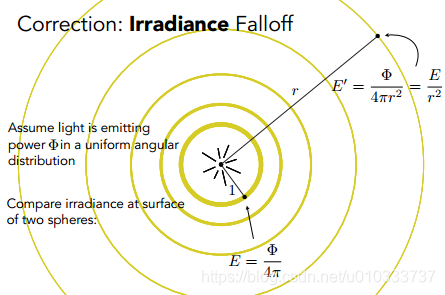
与之类似, 我们同样可以直接利用 Irradiance 的定义来解释为什么点光源会以距离平方的形式不断衰减. 同时这里我们可以进一步明确一点, 我们所说的衰减, 是 Irradiance 在衰减, Intensity 并不会衰减.
Radiance
Irradiance 告诉了我们表面上单位面积内接收到的 power 是多少. 这其中有一个关键的问题是 Irradiance 并没有体现出 power 在不同方向上的分布, 而光线追踪的过程明显是与方向相关的, 所以我们定义了 Radiance 来表达这一属性.
Radiance 是指辐射源在某一方向, 每单位投影面积, 每单位立体角内的 power.
接下来我们尝试使用"传输理论"来解释 Radiance 定义中的余弦项从何而来.
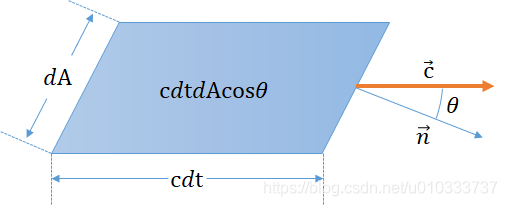
传输理论涉及物理量(如能量, 电荷, 质量)的传输或流动. 假设我们已知 x 处的光粒子密度为 p(x), 那么在一个很小的体积 dV 内光粒子的个数就是 p(x)dV. 下面再考虑这些粒子在时间 dt 内穿过一些不同的表面 dA. 假设光粒子的速度为 c, 那么这段时间内流过表面的体积就是 cdtdAcosθ, 那么穿过表面的粒子数量就是 p(x)cdtdAcosθ. 这很直观的说明了我们为什么要使用投影面积以及 radiance 中余弦项的来源.
参考资料
- 全局光照算法技术(第2版) (Advanced Global Illumination, 2nd Edition) Philip Dutre等著, 黄刚译
- Physically Based Rendering: From Theory To Implementation
- GAMES101-现代计算机图形学入门-闫令琪 Lecture 14 Ray Tracing 2
- PBRT-E5.4-辐射学（Radiometry） 知乎: 玉米
这篇关于【路径追踪】前置知识1--辐射度测量学 Radiometry的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
