基于UC3854的PFC仿真设计

本文主要是介绍基于UC3854的PFC仿真设计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

实习期间，老师要求我们完成一个单相PFC设计，要求指标如下：

输入电压 $220\pm15\%\mathrm{V_{rms}}$ ， $50\mathrm{Hz}$
输出电压平均值 $390\pm10\mathrm{V}$ ，纹波峰峰值不超过 $20\mathrm{V}$
容量 $3\mathrm{kW}$
网侧功率因数 $P F > 0.99$
网侧电流谐波 $THD<6\%$

经过简单选择，决定用PSIM带的UC3854进行设计仿真。一方面，UC3854面世时间早，资料多，TI官网还有有datasheet和参考设计，另一方面也是PSIM自带，省得再去找。
先简单介绍一下UC3854：
UC3854是1994年底TI公司推出的一款高功率因数预调节器，能够为电源提供有源功率因素校正。它能按正弦的电网电压来牵制非正弦的电流变化，该器件能最佳地利用供电电流使电网电流失真减到最小，执行所有PFC的功能。该器件适用于Boost型电路，采用平均电流控制方式，工作于CCM模式。其开关频率恒定，但可以通过外接电容电阻改变开关频率，最高可达 $200\mathrm{kHz}$ ；输出PWM波占空比最高可达 $95\%$ 。采用该器件控制时，可使电路功率因数达到 $0.99$ ，网侧电流谐波 $THD<5\%$ 。此外，该芯片还具有适用于任何的开关器件，采用通用的操作方式，无需开关；适用于全球电网电（ $80\sim 270\mathrm{V_{rms}}$ )；适用于广泛的频率范围（ $50\sim 400\mathrm{Hz}$ ）。具有前馈线性调整；噪声灵敏度低；内置低偏置模拟乘法器/除法器和高精度基准电压；输出驱动电压 $14.5\mathrm{V}$ ，输出驱动电流 $1\mathrm{A}$ ；具有软起动、输入电源欠压保护和输出过载保护功能的优点，使用广泛。
UC3854内部结构图如下图所示，其中主要包括欠压比较器、电压误差放大器、软起动逻辑、电网预置器、模拟乘法器、电流误差放大器、PWM比较器、三角波振荡器、过流比较器、 $7.5\mathrm{V}$ 参考电压、RS触发器和栅极驱动器等部分。其中，欠压比较器确保芯片供电高于 $16\mathrm{V}$ 时芯片正常工作；软起动逻辑用于实现芯片的软起动；过流比较器设置一个峰值电流限制，若电路中流过的电流超过设置的峰值电流值，则芯片关闭MOSFET；7.5V参考电压一方面用于电压误差放大器，一方面也可以作为一个稳定的基准电压输出；PWM比较器、三角波振荡器、RS触发器、山脊驱动器用于实现MOSFET驱动信号的输出。芯片的开关频率可以通过三角波振荡器外接的电容与电阻调整。电压误差放大器、电网预置器、模拟乘法器、电流误差放大器用于实现平均电流控制。
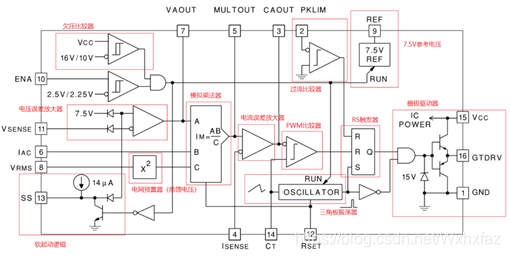
在这里插入图片描述
从数据手册给的说明来看，能满足设计要求，那就照着参考设计搭仿真电路。TI参考设计给出的电路如下：

考虑UC3854内部细节，电路图如下：

按我的理解，平均电流法控制需要两个控制环——电压环与电流环。上图中由 $R_{VI},R_{VD}$ 构成输出电压检测电路， $R_{vf},C_{vf},V_{REF}$ 和电压误差放大器构成PI控制，连接到模拟乘法器A输入构成电压控制环； $R_S$ 构成电流检测电路， $R_{MO},R_{ci},R_{cz},C_{cz},C_{cp}$ 与电流误差放大器构成的PI控制，与乘法器输出结合构成电流控制环。简化控制框图如下图所示。
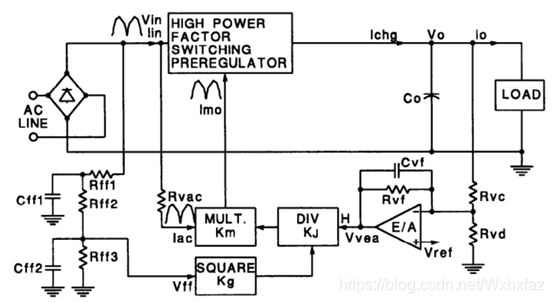
在这里插入图片描述
如上分析，UC3854采用了两个控制环，分别控制电流与电压。电流环由整流电压控制，使得输入电流能够跟随电压变化，实现功率因数校正的目标。电流控制信号由乘法器将整流器输出电压与电压误差放大器输出信号相乘得到，能够电流控制信号既能跟随整流器输出电压相位，其平均值大小又可以反映输出电压大小。电压环中还包含有一个平方器与一个乘法器，电压误差放大器输出信号在连接到模拟乘法器之前，首先与整流输出电压平均值的平方做除法。这一额外的电路能使电压回路的增益保持恒定。
基于TI参考设计搭建的UC3854仿真电路图如下：
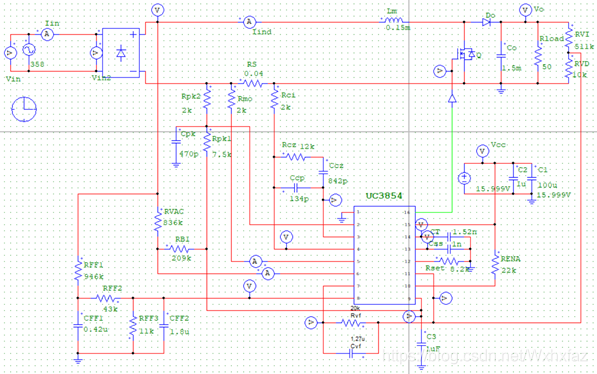
在这里插入图片描述
参考设计中是通过升压电感耦合了个变压器供电的，这里就直接用直流电源 $20\mathrm{V}$ 供电了。
跟着参考设计的步骤进行参数计算：
首先，考虑到计算过程误差，实际器件分散性和偶然因素等，需要留出一定的指标裕量，因此计算时采用的是下面的指标：

输入电压 $154\sim 270\mathrm{V_{rms}}$ ， $50\mathrm{Hz}$ （这里本来想搞 $220\pm 30\%\mathrm{V_{rms}}$ ，但是 $220\times 1.3=286>270$ ， $270$ 是数据手册说的适用于全球电网电压最高值，保险起见就搞到 $154\sim 270$ ）
输出电压平均值 $390\pm5\mathrm{V}$ ，纹波峰峰值不超过 $16\mathrm{V}$
容量 $3\mathrm{kW}$
网侧功率因数 $P F > 0.99$
网侧电流谐波 $THD<3\%$

开始计算参数：

选择开关频率：100kHz
计算电感：
1. 输入交流有效值最低为154V，输入电流最大峰值为 $I_{pk}=\frac{\sqrt{2}P}{V_{min}}=\frac{\sqrt{2}\times 3k}{154}\approx27.5496A$
2. 假定电流纹波为电流峰值的20%，则 $\Delta I=0.2\times I_{pk}\approx5.5099A$
3. 最小输入电压时，Boost电流占空比为 $D=\frac{V_{O}-V_{in}}{V_{O}}\approx0.4416$
4. 电感为 $L=\frac{V_{in}\times D}{f_{s}\Delta I}\approx0.1745mH$ ，取 $0.15 m H$
输出电容计算：

从输出电压纹波考虑，取输出电压纹波峰峰值为16V，代入 $V_{opk}=\frac{P}{2\pi f_{r}C_{O}V_{O}}$ ，得到 $C_{O}\approx1.5303mF$ ，取 $1.5 m F$ 。
确定电流检测电阻：
1. 输入电流最大峰值为 $I_{pk}=27.5496A$ ，考虑纹波，则最大可达 $I_{pk}+\frac{\Delta I}{2}\approx30.3046A$
2. 电流检测电阻压降一般为1V左右，得到 $R_{S}=\frac{1}{30.3046}\approx0.0330\Omega$ ，取 $R_{S}=0.04\Omega$ 。最大电流时压降为 $1.2122 V$
设定峰值电流限制：
1. $R_{pk1}$ 与 $R_{pk2}$ 用于设定峰值电流，满足 $R_{pk2}=\frac{V_{rs}R_{pk1}}{V_{REF}}$ ，其中 $V_{REF}=7.5V$
2. 考虑到电流最高可能达到 $30.3046 A$ ，可设峰值电流为 $50 A$ ，则 $V_{rs}=50\times 0.04=2V$
3. 取 $R_{pk2}=7.5k$ ，则 $R_{pk1}=\frac{2\times 7.5}{7.5}=2k$
4. $C_{pk}$ 为一小电容，可以抗噪并适当提高峰值电流，此处取典型电路中的值 $470 p$ 。
前馈电压设置：
1. 前馈电压由 $R_{ff1}, R_{ff2}, R_{ff3}$ 于 $C_{ff1}, C_{ff2}$ 构成的二阶低通滤波电路分压得到，需要满足两个条件：最高输入电压时， $V_{ff}<4.5V$ ，最低输入电压时 $V_{ff}\approx1.414V$ ，且分压器 $R_{ff2}+R_{ff3}$ 上压降近似为7.5V，于是得到：
  $\frac{R_{ff3}}{R_{all}}\times 154\times 0.9=1.414\\ \frac{R_{ff3}+R_{ff2}}{R_{all}}\times 154\times 0.9=7.5\\$
2. 取 $R_{all}=1M$ ，得到 $R_{ff3}\approx10.2020k$ ， $R_{ff2}\approx43.9105k$ ， $R_{ff1}\approx945.8875k$
3. 取 $R_{ff1}=11k$ ， $R_{ff2}=43k$ ， $R_{ff3}=946k$ ，检验满足要求
输入电流设置：
1. 输入电流最高工作于 $0.6 m A$ ，为使乘法器线性度较好，令输入电压最高时，输入电流为 $0.45 m A$ ，于是得到 $R_{vac}=\frac{270\times \sqrt{2}}{0.45m}\approx848.5271k$ ，取 $836 k$ 。
2. $R_{b1}$ 为 $\frac{R_{vac}}{4}$ ，取 $209 k$ 。
输出电流限制：
1. 输出电流满足 $I_{mo}<\frac{3.75}{R_{set}}$ ，最小输入电压时， $I_{mo}$ 最大，令 $I_{mo}=\frac{3.75}{R_{set}}$ 得到 $R_{set}=\frac{3.75}{2I_{ac}}\approx7.1973k$ ，取 $8.2 k$
2. 最小输入电压时 $R_{mo}$ 上压降近似与 $R_{s}$ 相同，得到 $R_{mo}=\frac{V_{rspk}}{2I_{ac}}\approx1.4255k$ ，取2k
振荡电容确定： $C_{t}=\frac{1.25}{R_{set}\times f_{s}}\approx1.5244nF$ ，取 $1.52 n F$
电流误差放大器补偿：
1. $R_{S}$ 上压降斜率最大值为 $\frac{V_{O}\times R_{S}}{L}=104mV/\mu s$ ，工作与 $100 k H z$ 时内部三角波斜率为 $0.52V/\mu s$ ，则电流误差放大器增益为 $gain=\frac{0.52}{0.104}=5$ ，取 $R_{ci}=R_{mo}=2k$ ，则 $R_{cz}=gain\times R_{ci}=10k$ ，取 $12 k$
2. 电流环交叉频率为 $f_{ci}=\frac{V_{O}\times R_{S}\times R_{cz}}{2\pi L\times V_{s}\times R_{ci}}\approx19.0986kHz$ ，考虑零点配置，取 $C_{cz}=\frac{1}{2\pi f_{ci}R_{cz}}\approx694.4444p$ ，取 $842 p$ ；考虑极点配置，取 $C_{cp}=\frac{1}{2\pi f_{s}R_{cz}}\approx132.6291p$ ，取 $134 p$
电压误差放大器补偿
1. 输出电压纹波 $V_{opk}=\frac{P}{2\pi f_{r}C_{O}V_{O}}\approx8.1618V$
2. 假定分配电压误差放大器输出电压纹波为0.5%，则最大输出纹波为 $\Delta V_{vea}\times 0.5\%=20mV$ ，增益应该为 $G_{va}=\frac{\Delta V_{vea}}{V_{opk}}\approx0.002450$
3. 取 $R_{vi}=511k$ ，则 $C_{vf}=\frac{1}{2\pi f_{r}R_{vi}G_{va}}\approx1.2710\mu$ ，取 $1.27\mu$
4. $R_{vd}=\frac{R_{vi}V_{REF}}{V_{O}-V_{REF}}\approx10.0196k$ ，取 $10 k$
5. 电压环增益为一时，频率为 $f_{vi}^2=\frac{P}{4\pi^2\Delta V_{vea}V_{O}R_{vi}C_{O}C_{vf}}$ ，代入解得 $f_{vi}\approx7.0711Hz$
6. $R_{vf}=\frac{1}{2\pi f_{vi}C_{vf}}\approx17.7084k$ ，取 $17.7 k$
前馈电压滤波电容
1. 假定分配到前馈电压上纹波百分比为 $0.5\%$ ，则 $G_{ff}=\frac{0.5}{66.2}\approx0.007553$ ， $f_{p}=\sqrt{G_{ff}}f_{r}\approx8.6907Hz$
2. $C_{ff1}=\frac{1}{2\pi f_{p}R_{ff2}}\approx0.4147\mu$ ， $C_{ff2}=\frac{1}{2\pi f_{p}R_{ff3}}\approx1.7951\mu$ ，取 $C_{ff1}=0.42\mu$ ， $C_{ff2}=1.8\mu$
此外，电压VCC通过两个滤波电容连接到输出电压为 $V C C$ 的直流电压源上，ENA通过一 $22 k$ 的电阻连接到VCC拉高，SS通过一个 $1 n F$ 电容旁路到GND， $V_{REF}$ 通过一个 $1\mu F$ 电容旁路到GND。

仿真结果：
输入 $220\mathrm{V_{rms}}$ 时，仿真波形（从上到下依次是网侧电压电流，输出电压，网侧电流）如下：
在这里插入图片描述
可以看到起始阶段电流有一个过冲，输出电压有一个超调。这应该是初始阶段输出电容初始电压为零，上电时等效为短路，所以电流过冲。稳态时波形：

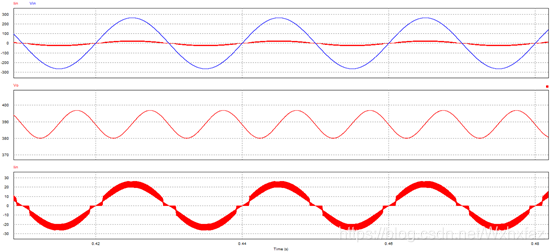
测量值：

此时输入功率因数达到 $0.9919$ ，输出电压平均值为 $388.5619\mathrm{V}$ ，此时，输出功率为 $\frac{388.5619^2}{50}=3.020\mathrm{kW}$ ，且输出纹波峰峰值不超过 $20\mathrm{V}$ ，已经满足要求，但是网侧电流 $THD=12.84\%>6\%$ ，仍不能满足要求。观察输出电流波形可以看到，电流谐波较大的原因主要来自于两点，一为较大的电流开关频率纹波，其频率较高，另一为电流波形过零点时较大的畸变。

这就很奇怪，明明是按照TI参考设计过程计算的，怎么电流 $T H D$ 这么大呢？
嗯，或许是计算电感时，预设的电流纹波 $20\%$ 过大了，改小一下，再看看：
仿真电路：
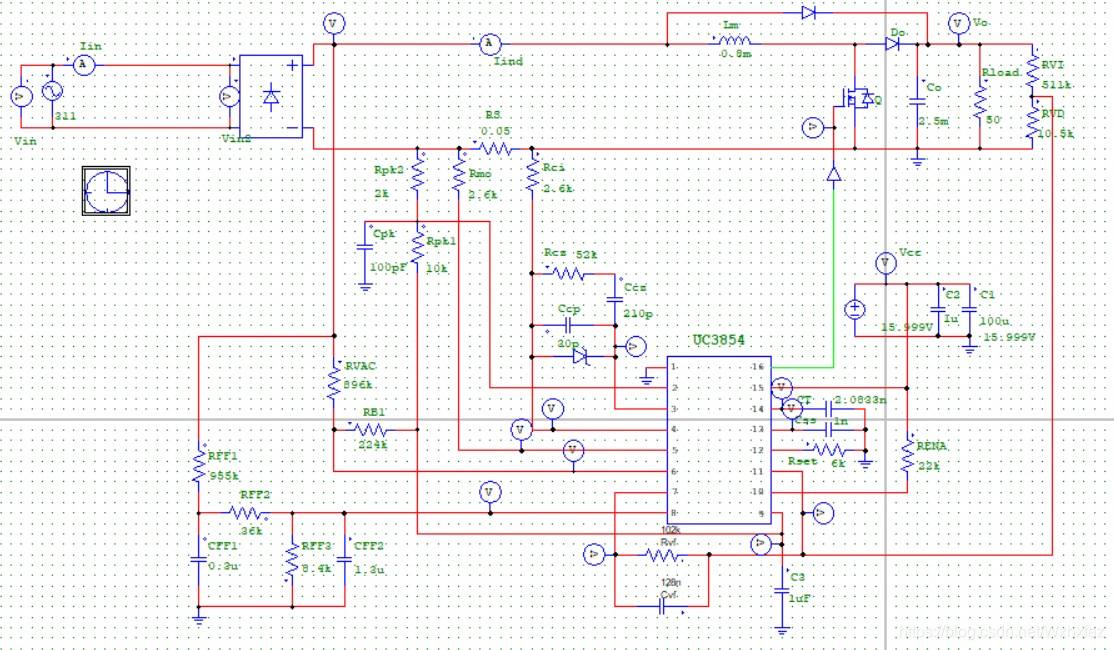
在这里插入图片描述
仿真波形：

稳态波形：

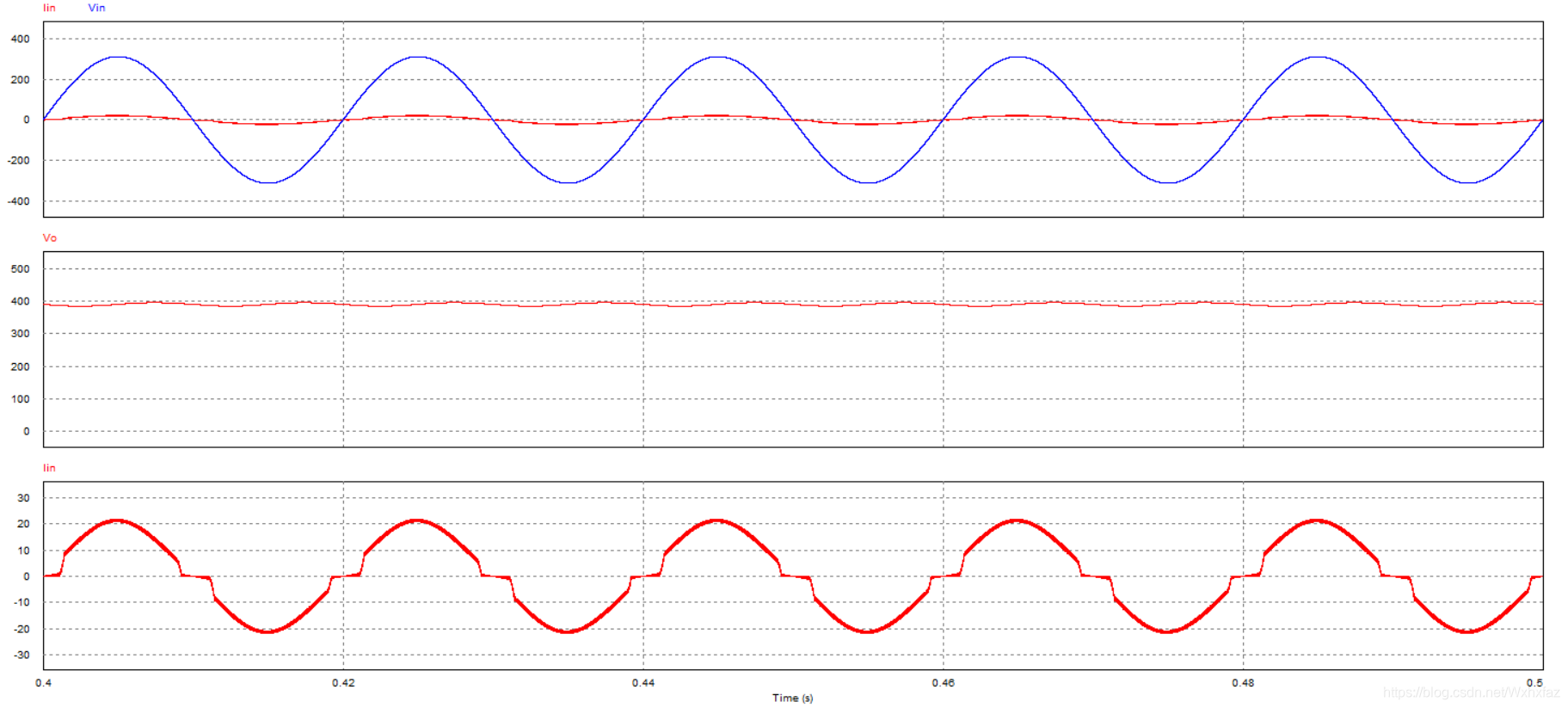
额，虽然网侧电流高频分量小了，但是电流过零畸变更严重了。调节电流环参数影响不大。猜测是电流过零畸变本来就是平均电流法控制固有的一种现象，而且UC3854PWM最高只能输出 $95\%$ 占空比。当电流纹波小时，过零点时波动也小，较长一段时间内都冲不过去，反而电流纹波大一些有助于冲过过零点。
可是这指标怎么搞呢？TI明明声称 $THD<5\%$ 啊。无奈之下，又把TI的参考设计给仿真了一遍，发现它的波形也差不多：
在这里插入图片描述

这么大的电流纹波怎么可能 $THD<5\%$ 呢？
在这里插入图片描述
再去看数据手册和参考设计，发现TI参考设计测定 $T H D$ 时只测到50倍基波频率。那么电流里面的高频分量直接就被无视了。

既然如此，我就不纠结调参数降低 $T H D$ 了，就在输入侧加个低通滤波器算了。顺便为了解决起始阶段电流过冲问题，串入电阻再逐级切除。仿真电路如下：
在这里插入图片描述
仿真波形：

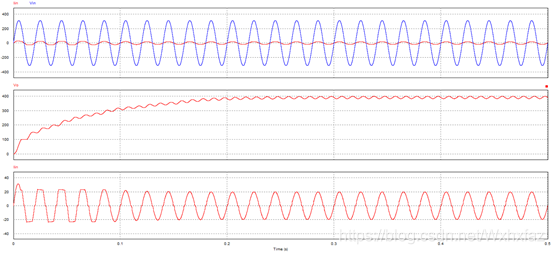
可以看到，起始阶段电流过冲基本消失，输出电压超调也没了，但是调节时间变长了。稳态时测量指标，都满足了（输入 $220\times (1-15\%)=187\mathrm{V_{rms}}$ 时电流 $THD=5.9\%$ 有点惊险，但是输入 $220\mathrm{V_{rms}}$ 时为 $3.8\%$ ，输入 $220\times (1+15\%)=253\mathrm{V{rms}}$ 时为 $1.66\%$ 还是都不错的）
电流THD还是较大的原因主要就是电流过零畸变了，但是设计任务完成了，这一问题以后有空再解决吧。
模型链接

=====================================================================
评论里关于第十二步的66.2怎么来的，可以看一下TI的参考设计
在这里插入图片描述

在这里插入图片描述
这里的66.2%是一个常数（应该是经过整流桥后的|sin|的一个特性，我暂时没想通是怎么得到的，|sin(x)|的二次谐波分量为 $\frac{4}{3\pi}$ ，平均值（即零频率分量）为 $\frac{2}{\pi}$ ，那么二次谐波分量应该是 $\frac{2}{3}\approx0.667$ ，不知道有没有关系）。
参考手册我也上传一下，需要的可以下载看看。
TI参考设计