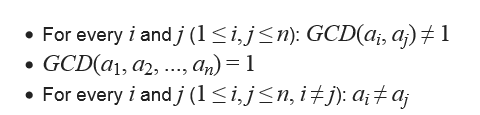Codeforces - 66D - Petya and His Friends（数论质数+思维）

题目：

Little Petya has a birthday soon. Due this wonderful event, Petya's friends decided to give him sweets. The total number of Petya's friends equals to n.

Let us remind you the definition of the greatest common divisor: GCD(a1, ..., ak) = d, where d represents such a maximal positive number that each ai (1 ≤ i ≤ k) is evenly divisible by d. At that, we assume that all ai's are greater than zero.

Knowing that Petya is keen on programming, his friends has agreed beforehand that the 1-st friend gives a1 sweets, the 2-nd one gives a2sweets, ..., the n-th one gives an sweets. At the same time, for any i and j (1 ≤ i, j ≤ n) they want the GCD(ai, aj) not to be equal to 1. However, they also want the following condition to be satisfied: GCD(a1, a2, ..., an) = 1. One more: all the ai should be distinct.

Help the friends to choose the suitable numbers a1, ..., an.

Input

The first line contains an integer n (2 ≤ n ≤ 50).

Output

If there is no answer, print "-1" without quotes. Otherwise print a set of n distinct positive numbers a1, a2, ..., an. Each line must contain one number. Each number must consist of not more than 100 digits, and must not contain any leading zeros. If there are several solutions to that problem, print any of them.

Do not forget, please, that all of the following conditions must be true:

• For every i and j (1 ≤ i, j ≤ n): GCD(ai, aj) ≠ 1
• GCD(a1, a2, ..., an) = 1
• For every i and j (1 ≤ i, j ≤ n, i ≠ j): ai ≠ aj

Please, do not use %lld specificator to read or write 64-bit integers in C++. It is preffered to use cout (also you may use %I64d).

Examples

input

3

output

99
55
11115

input

4

output

385
360
792
8360

题意：要求构造一个长度为n的正整数序列,满足以下条件：

题解：

很容易想到，任意两个数之间GCD=1那么就是说明他们互质的，那么对于三个数a b c，如果a b的最大公约数x不为1，b c的最大公约数y不为1，而a b c三个的最大公约数为1，就是说明x与y是互质的，那么这样才能满足任意多个数的gcd不为1且互质呢，我们知道质数为2 3 5 7......，那么我们选第一个数为2*3，第二个数与它的gcd为2，那么选取第二个数为2*5，但是还需要一个数与第一个，第二个的gcd不为1，但三个总的gcd为1，那么如果我选择第三个数与第一个数的gcd是2，那么显然是不可以的，因为第二个与第一个的gcd也是2，所以他们三个的gcd是2不是1，所以我们只能选择第三个与第一个的gcd为3，那么第三个与第二个的gcd只能选择5了，这样三个数2*3，2*5 ,  3*5，他们满足两两gcd不为1，但三者的gcd为1，那么我前三个已经满足总的gcd为1了，后面的就只要找，与他们三个都互质了的，那么我们可以选择2*3的倍数，这样与（2*5）的gcd至少会是2，与（3*5）的gcd至少会是3，但是前面的2*3，2*5，3*5已经保证满足总的gcd为1,了，所以后面只要选择三个中任意一个的倍数就好了，不需要高精度，不需要long long，不需要STL等，代码也很短，只要11行！！！

代码：

#include<bits/stdc++.h>
using namespace std;
int n;
int main()
{   scanf("%d",&n);if(n==2){printf("-1");return 0;}printf("6\n10\n15\n");for(int i=4;i<=n;i++)printf("%d\n",2*3*(i-2));return 0;
}