1287. 躲雨

Description

　　FJ的奶牛真的很怕雨，所以一下雨他们就急着要找地方躲雨。为了做好防雨准备，他们装了警报器，一有雨就拉响警报器，他们利用天气预报来预测雨的到来，但有时候不准导致拉错警报，为了减少拉错警报的可能，他们想在保证奶牛有足够时间躲起来的前提下尽可能晚地拉响警报。
　　农场有F(1<=F<=200)个奶牛吃草的区域，有P(1<=P<=1500)条路连接一些区域，路是双向的。有些区域有遮雨棚，每个遮雨棚有自己的容量限制。
　　现在要你计算所有牛都能找到地方躲雨最少需要多少时间。

Input

　　第1行：两个空格隔开的整数F和P
　　第2到F+1行：每行两个空格隔开的整数X,Y，X表示当前这个区域的牛的数量，Y表示该区域的遮雨棚最多只能容纳Y头牛。
　　第F+2到F+P+1行：3个空格隔开的整数a,b,c,表示a和b之间有一条长度为c的路直接相连。

Output

　　输出一个整数，表示所有牛都能在这个时间内到达遮雨棚。

Sample Input

3 4
7 2
0 4
2 6
1 2 40
3 2 70
2 3 90
1 3 120

Sample Output

110

Data Constraint

Hint

【样例说明】
　　1号区域里保留2头牛，4头牛去2号区域，还有1个去3号区域，3号区域的2头牛保持不动，可能还有其他方案，但110是最少的时间。

Source / Author: USACO

题解：

二分，二分图匹配。

有一种方法是把每个节点拆开成x[i]+y[i]个来匈牙利，但匈牙利O（n+m）。

考虑网络流。

先预处理dis[i][j]为i到j的距离。

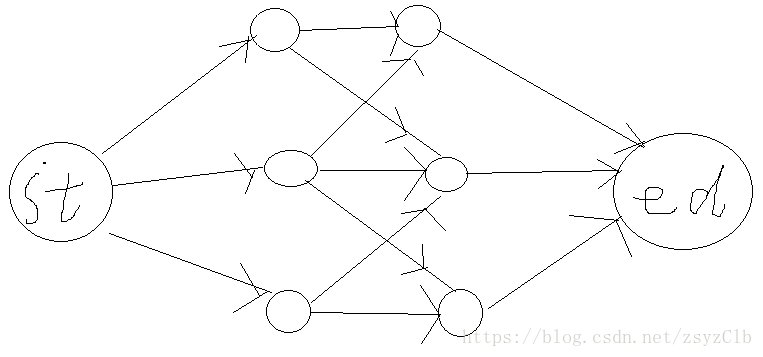
建图：

原点给1～n 点连一条流量为x的边。

汇点给1'~n'连一条流量为y的边。

1～n 给 1'~n'  连一条流量为INF的边。

（条件：若i要给j一条边，则dis[i][j]<=mid）

然后做一次最大流。

1. 初始弧优化
2. 分层图优化 
3. gap优化

最大流sap算法：详见：https://blog.csdn.net/Com_man_der/article/details/94645092

初始弧：

dg中记录一个点走到哪条边了，下次只用接着往后枚举。

分层图优化 ：

所谓距离标号 ，就是某个点到汇点的最少的弧的数量dis，走的时候只走允许弧（dis[i] = dis[j+1] i----->j）

gap优化：

gap[i]数组表示距离标号为i的点有多少个，如果到某一点没有符合距离标号的允许弧，那么需要修改距离标号来找到增广路； 如果重标号使得gap数组中原标号数目变为0，则算法结束。

1. #include<bits/stdc++.h>
   #define mem(a,b) memset(a,b,sizeof(a))
   #define ll long long
   #define rint register int
   #define N 2010
   #define M 500010
   #define open(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
   #define INF 2147483647
   using namespace std;struct edge
   {ll v,fr,d,t; ll c;};//注意d是不变的，c是剩余流量 ll n,m,i,j,k,t,ans,tmp1,tmp2;
   ll x[N],y[N];
   ll l,r,mid;
   ll tail[N],tot=1; edge e[M];
   ll dis[N],gap[N],cur[N],S,T;
   ll floyd[N][N];void init_dis()
   {for(rint i=1;i<=n;i++)floyd[i][i]=0;for(rint k=1;k<=n;k++)for(rint i=1;i<=n;i++)for(rint j=1;j<=n;j++)(floyd[i][j] = min(floyd[i][j] , floyd[i][k] + floyd[k][j]));return ;
   }void add(ll u,ll v,ll d,ll t)
   {e[++tot].v=v;e[tot].d = e[tot].c = d;e[tot].t=t;e[tot].fr=tail[u];tail[u]=tot;
   }void turn_back()
   {for(rint i=2;i<=tot;i++)e[i].c=e[i].d;return ;
   }void build_graph()
   {for(i=1;i<=n;i++)add(0,i,x[i],0),add(i,0,0,0);//for(i=1;i<=n;i++)for(j=1;j<=n;j++) add(i,j+n,INF,floyd[i][j]),add(j+n,i,0,floyd[j][i]);//for(i=1;i<=n;i++)add(i+n,2*n+1,y[i],0) , add(2*n+1,i+n,0,0);//return ;// 最后的点数为1+n+n+1 : 0 -- 2*n+1 ; 0为源点 ； n*2+1为汇点。 
   }ll dfs(ll k,ll flow)
   {if(k==T)return flow;ll have=0;for(ll p=cur[k];p;p=e[p].fr)if(e[p].t <= mid){ll &v=e[p].v,&c=e[p].c;if(dis[k] -1 == dis[v] && c){cur[k] = p;ll now = dfs(v, min(flow - have,c));c-= now;e[p^1].c+=now;have+=now;if(have == flow)return flow;}}	cur[k] = tail[k];if(!(--gap[dis[k]])) dis[S]=T;gap[++dis[k]]++;return have;
   }ll check()
   {mem(gap,0);mem(dis,0);rint i=0,j=0;S=0,T=n*2+1;for(i=0;i<=T;i++)cur[i] = tail[i];turn_back();gap[0] = T+1;while(dis[S] < T+1) dfs(S,INF);ll p =tail[0];for( ;p;p=e[p].fr)if(e[p].c>0) break;return !p;
   }void binary()
   {l=0;r=r;ans=-1;while(l<=r){mid=(l+r)/2;if(check()){ans = mid;r = mid-1;}else l=mid+1;}return ;
   }int main()
   {open("rain");scanf("%lld%lld",&n,&m);for(i=1;i<=n;i++)scanf("%lld%lld",&x[i],&y[i]);ll u,v,d;mem(floyd,60);for(i=1;i<=m;i++)scanf("%lld%lld%lld",&u,&v,&d),(floyd[u][v]=floyd[v][u]=min(floyd[v][u],d)),r+=d;init_dis();build_graph();binary();printf("%lld",ans);return 0;	
   }