caioj.cn 1118:网络流入门4：牛躲雨

输出解释：110是最短的时间。牛棚1安排4头牛到牛棚2，牛棚1再安排1头牛走到牛棚2，再走到牛棚3 避雨。这样最少的时间就是110。

这一道题一眼似乎看不出是什么算法，但是我找不出有什么算法能直接求出时间，于是我就用二分查找时间，用网络流判断是否可行，找路径就用floyd

难点在网络流（不用说了）

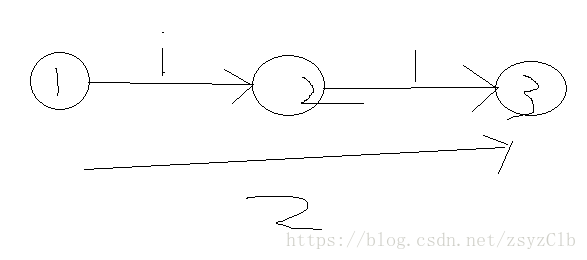
如果直接用网络流，就会存在一个问题

如果限制路径长为1，那么就会有（最短路径）1->2 ，有从2->3，这样就不是我们需要找的路径，因此我们需要拆点

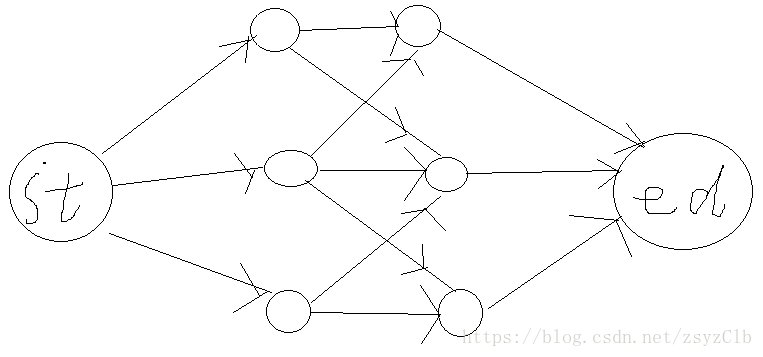
拆完点后就会变成这样（样例）:

我画的图片有点丑，不要介意

在每次判断中：

定义原点和汇点

从原点建边到第一个点，流量为原来牛的个数

从第二个点建边倒终点，流量为可以容纳的牛的数量，这样可以很好的控制牛棚里牛的数量

从第一个点建边到第二个点，流量为无限大

最后双重for枚举两个点，从第一组点的第一个点连接到第二组点的第二个点，因为第二个点只能通向终点，所以不会出现刚才说的那种情况，注意有双向边（建两次即可），建立的边都不超过查找的时间

跑一次网络流，表示最后能到达终点（进入牛棚的牛的个数）

建图的思路理清了，代码就很好理解了：

#include<cstdio>
#include<cstring>
using  namespace  std;
typedef long long ll;
struct  node
{int  x,y,c,next,other;
}a[210000];int  len,last[21000],n,m,st,ed,A,aa[2100],bb[2100];
ll  map[210][210];
inline int mymin(int  x,int  y){return x<y?x:y;}
inline void ins(int x,int y,int c)
{int k1,k2;len++;k1=len;a[len].x=x;a[len].y=y;a[len].c=c;a[len].next=last[x];last[x]=len;len++;k2=len;a[len].x=y;a[len].y=x;a[len].c=0;a[len].next=last[y];last[y]=len;a[k1].other=k2;a[k2].other=k1;
}
int list[2100],head,tail,h[2100];
inline bool bt_h()
{memset(h,0,sizeof(h));h[st]=1;head=1;tail=2;list[head]=st;while(head!=tail){int  x=list[head];for(int  k=last[x];k;k=a[k].next){int  y=a[k].y;if(h[y]==0  &&  a[k].c>0){h[y]=h[x]+1;list[tail++]=y;}}head++;}if(h[ed]>0)return  true;return  false;
}
int find(int x,int f)
{if(x==ed)return f;int s=0,t;for(int k=last[x];k;k=a[k].next){int  y=a[k].y;if(h[y]==h[x]+1 && a[k].c>0 && s<f){s+=(t=find(y,mymin(f-s,a[k].c)));a[k].c-=t;a[a[k].other].c+=t;}}if(s==0)h[x]=0;return  s;
}
inline bool check(ll x)
{len=0;memset(last,0,sizeof(last));//每次都要初始化 for(int i=1;i<=n;i++){ins(st,i,aa[i]);//起点到第一个点 ins(i+n,ed,bb[i]);//第二个点到终点 ins(i,i+n,A);//左右两点之间的边 }for(int i=1;i<n;i++)//建立不同点之间的边 for(int j=i+1;j<=n;j++)if(map[i][j]<=x)ins(i,j+n,A),ins(j,i+n,A);//建立的是最短的路径 int ans=0;while(bt_h()==true) ans=ans+find(st,999999999);//找最大流（最多有几只牛能到达牛棚） if(ans==A) return true;//如果所有的牛都进入了牛棚 return false;
}
int main()
{scanf("%d%d",&n,&m);st=0;ed=2*n+1;//原点和终点 memset(map,1,sizeof(map));//两点的距离 for(int i=1;i<=n;i++)scanf("%d%d",&aa[i],&bb[i]),A+=aa[i],map[i][i]=0;//输入和初始化，A表示牛的只数 for(int i=1;i<=m;i++){ll c;int x,y;scanf("%d%d%lld",&x,&y,&c);if(map[x][y]>c) map[x][y]=map[y][x]=c;//可能有多条边 }for(int k=1;k<=n;k++)//标准的五行floyd代码 for(int i=1;i<=n;i++)	for(int j=1;j<=n;j++)if(map[i][j]>map[i][k]+map[k][j])map[i][j]=map[i][k]+map[k][j];ll  l=1,r=ll(999999999999999),mid;//初始化无限大 while(l<=r)//二分查找 {mid=(l+r)/2;if(check(mid)==true)r=mid-1;//如果可以的话，就尝试这缩小时间 else  l=mid+1;}if(r==ll(999999999999999))printf("-1\n");//如果没有成功的查找过 else{if(check(r)==true)printf("%lld\n",r);//首选r是因为最后r<l else  printf("%lld\n",l);//输出 }   return 0;	
}