本周图论的flod和dij算法

本文主要是介绍本周图论的flod和dij算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第一题

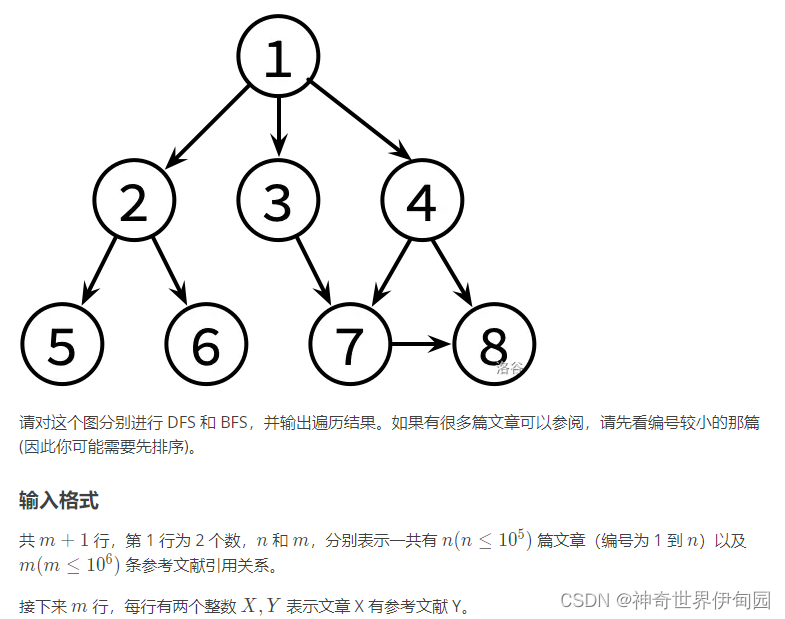
输入 #1

输出 #1

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8

解读：

中规中矩的图论题，记得这个题需要排序，写一个dfs和bfs就好，要用到vis数组，还有这题可以直接用vector来存储节点信息，（vector是首要选择的数据结构），我们也可以为了插入节点方便使用list，deque，都是可以过去的，但是更建议用vector

#include <bits/stdc++.h>
using namespace std;const int max_n = 100002;deque<int> ins[max_n];
bool vis[max_n] = {0};void dfs(int s)
{cout << s << ' ';for(int x: ins[s]){if(!vis[x]){vis[x] = true;dfs(x);}}
}
queue<int> nodes;
void bfs(int s)
{cout << s << ' ';nodes.push(s);while(!nodes.empty()){int top = nodes.front();nodes.pop();for(int x: ins[top]){if(!vis[x]){cout << x << ' ';nodes.push(x);vis[x] = true;}}}
}
int main()
{int n, m;cin >> n >> m;int a, b;for(int i = 1; i <= m; i++){cin >> a >> b;ins[a].push_back(b);}for(int i = 1; i <= n; i++){sort(ins[i].begin(), ins[i].end());}vis[1] = true;dfs(1);memset(vis, 0, sizeof(vis));vis[1] = true;cout << endl;bfs(1);return 0;
}

第二题

输入 #1

2 1
1 2 4

输出 #1

4 4

输入 #2

输出 #2

这题就是弗洛伊德算法的模板题，弗洛伊德算法是一种动态规划算法，本质是还是蛮力的循环遍历算法，适合群体求解图论中最短路径问题。以下是题解。其中dis[i][j]表示i到j之间的最短路径，我们只需要在所有可能的中间点情况中找到一个合适的中间点来使得dis[i][j]最小，所以我们可以写出以下的递推方程：dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j])，k的循环要写在外面。参考课程

懒猫老师-数据结构-(48)最短路径(Floyd算法，弗洛伊德算法，多源最短路径)_哔哩哔哩_bilibili

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define max_n 502
#undef INT_MAX
#define MMAX (int)(1E9+2)
int dis[max_n][max_n] = {MMAX};		//小心这个数组的初始化 
signed main()
{int n, m;cin >> n >> m;//初始化，0的已经完成了 for(int i = 0; i <= n; ++i){for(int j = 0; j <= n; ++j){if(i == 0 || j == 0)dis[i][j] = 0;else if(i == j)dis[i][j] = 0;elsedis[i][j] = MMAX;}}//输入元素 for(int i = 1; i <= m; ++i){int a, b, c;cin >> a >> b >> c;dis[a][b] = min(dis[a][b], c);dis[b][a] = min(dis[b][a], c);}//开始进行算法for(int k = 1; k <= n; ++k){for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j]);}}}//准备输出for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){if(dis[i][j] != MMAX)dis[i][0] = (dis[i][j]+dis[i][0])%998244354;}cout << dis[i][0] << endl; }return 0;
}

第三题

地杰斯特拉算法：

输入 #1

输出 #1

0 2 4 3

就看这些就够了，这个是模板题，直接给出答案

#include <bits/stdc++.h>
#define int long long 
using namespace std;		//链式前向星 
const int max_m = 2*1E5+2;
const int max_n = 1E5+2;
const int inf = 0x3f3f3f3f;
struct edge
{int w, to, next;		//数值，到达节点，下一波 
};
struct node
{int w, now;				//距离和当前节点 bool operator< (const node &x) const{return w > x.w;}
};
edge arr[max_m];			//前向星的链表
int head[max_n] = {0};		//头结点的指针 
int cnt;					//当前第几条边 
bool vis[max_n] = {0};
int dis[max_n] = {inf};		//距离这个初始化不管用啊 
priority_queue<node> q;	//优先队列 
void push_node(int s, int to, int w)
{arr[++cnt] = (edge){w, to, head[s]}, head[s] = cnt;
}
void dijkstra(int start)
{dis[start] = 0;				//先把开始点0q.push((node){0, start});	//第一个点到start是0while(!q.empty()) {node tmp = q.top();q.pop();int x = tmp.now, d= tmp.w;if(!vis[x]){vis[x] = true;for(int i = head[x]; i; i = arr[i].next){int y = arr[i].to;if(dis[y] > dis[x] + arr[i].w){dis[y] = dis[x] + arr[i].w;if(!vis[y]){q.push((node){dis[y], y});}}}}}
}
signed main()
{int n, m, s;			//s是起始节点 cin >> n >> m >> s;for(int i = 1; i <= m; ++i) {int a, b, c;cin >> a >> b >> c; push_node(a, b, c);}memset(dis, inf, sizeof(dis));dis[s] = 0;// vis[s] = 1;	//准备工作dijkstra(s);for(int i = 1; i <= n; ++i){cout << dis[i] << ' ';}return 0;
}

这是地杰斯特拉的堆优化算法，使用优先队列（优先队列可以自动排序，内部采用二叉树存储，可以提高访问效率），做法和bfs一致（地杰斯特拉算法本质是就是一种贪心算法），然后的话就是这个初始化部分，这里可以不初始化，vis[s]=1，因为这个点先被送进队列然后才被访问的，当然这里是否初始化要看你的代码。还有的就是这个数组在外面初始化inf居然不管用，还得在memset一次，真是奇怪了。还要注意的是这个要写一个运算符重载，优先队列就很奇怪，明明是小于却要用大于来重载，记住就好。

这篇关于本周图论的flod和dij算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！