图论06-【无权无向】-图的遍历并查集Union Find-力扣695为例

本文主要是介绍图论06-【无权无向】-图的遍历并查集Union Find-力扣695为例，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

1. 代码仓库
2. 思路
- 2.1 UF变量设计
- 2.2 UF合并两个集合
- 2.3 查找当前顶点的父节点 find(element)
3. 完整代码

1. 代码仓库

https://github.com/Chufeng-Jiang/Graph-Theory

2. 思路

2.1 UF变量设计

在这里插入图片描述

parent数组保存着每个节点所指向的父节点的索引，初始值为当前顶点编号，指向自己。

后期在合并的时候均指向其合并的另一个元素的父节点，也就是p->a, q->q,合并p和q时，改变q的指向，q->a.

最终a下面挂两个节点，分别为p, q.

//parent数组中保存着每个节点所指向的父节点的索引
private int[] parent;sz数组来保存每个根节点所代表的子树中元素的数量 
private int[] sz;

2.2 UF合并两个集合

查找两个元素的父节点，父节点相同则属于同一个集合

public void unionElements(int p, int q) {int pRoot = find(p); // 找到p的父节点int qRoot = find(q); // 找到q的父节点if (pRoot == qRoot) // 如果pq的父节点相同，说明在同一个集合内return;parent[pRoot] = qRoot; //如果不相同，将p的父节点挂到q的父节点下，进行合并sz[qRoot] += sz[pRoot]; //q的集合大小合并
}

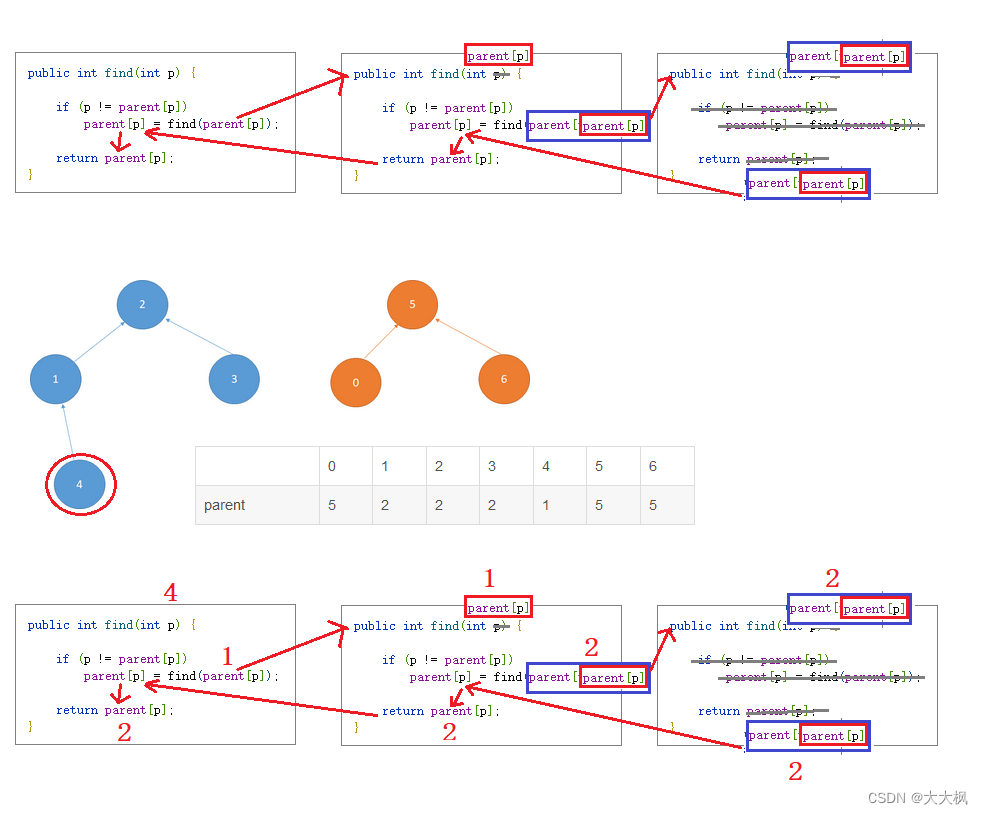
2.3 查找当前顶点的父节点 find(element)

递归查找父节点，只要不满足p = parent[p]，就肯定没有到达最上层。find(parent[p])为查找p节点的

public int find(int p) {if (p != parent[p]) //还没找到根节点parent[p] = find(parent[p]); //递归实现//p = parent[p]时，就是父节点return parent[p]; 
}

在这里插入图片描述

3. 完整代码

public class Union_Find {class UF {private int[] parent; //parent数组中保存着每个节点所指向的父节点的索引private int[] sz;public UF(int n) {parent = new int[n];sz = new int[n];for (int i = 0; i < n; i++) {parent[i] = i; //初始化的时候当前节点的父节点都是自己sz[i] = 1; //当前所属集合的大小}}// 不断去查询自己的父亲节点, 直到到达根节点// 根节点的特点: parent[p] == ppublic int find(int p) {if (p != parent[p]) //还没找到根节点parent[p] = find(parent[p]); //递归实现return parent[p]; //终于找到根节点}public boolean isConnected(int p, int q) {return find(p) == find(q);}public void unionElements(int p, int q) {int pRoot = find(p); //找到p的父节点int qRoot = find(q); //找到q的父节点if (pRoot == qRoot)//如果pq的父节点相同，说明在同一个集合内return;parent[pRoot] = qRoot; //如果不相同，将p的父节点挂到q的父节点下，进行合并sz[qRoot] += sz[pRoot]; //q的集合大小合并}public int size(int p) {return sz[find(p)];}}private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};private int R, C;public int maxAreaOfIsland(int[][] grid) {if (grid == null) return 0;R = grid.length;if (R == 0) return 0;C = grid[0].length;if (C == 0) return 0;UF uf = new UF(R * C);for (int v = 0; v < R * C; v++) {int x = v / C, y = v % C;if (grid[x][y] == 1)for (int d = 0; d < 4; d++) {int nextx = x + dirs[d][0], nexty = y + dirs[d][1];if (inArea(nextx, nexty) && grid[nextx][nexty] == 1) {int next = nextx * C + nexty;uf.unionElements(v, next);}}}int res = 0;for (int v = 0; v < R * C; v++) {int x = v / C, y = v % C;if (grid[x][y] == 1)res = Math.max(res, uf.size(v)); //遍历找到最大的size}return res;}private boolean inArea(int x, int y) {return x >= 0 && x < R && y >= 0 && y < C;}
}