Codeforces Round #847 (Div. 3) A-F题讲解

本文主要是介绍Codeforces Round #847 (Div. 3) A-F题讲解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻讲解一下Codeforces Round #847 (Div. 3)这场比赛的A-F题！

===========================================================================================

A题——Polycarp and the Day of Pi

原题

On March 14, the day of the number π is celebrated all over the world. This is a very important mathematical constant equal to the ratio of the circumference of a circle to its diameter.

Polycarp was told at school that the number π is irrational, therefore it has an infinite number of digits in decimal notation. He wanted to prepare for the Day of the number π by memorizing this number as accurately as possible.

Polycarp wrote out all the digits that he managed to remember. For example, if Polycarp remembered $π$ as $3.1415$ , he wrote out $31415$ .

Polycarp was in a hurry and could have made a mistake, so you decided to check how many first digits of the number $π$ Polycarp actually remembers correctly.

Input
The first line of the input data contains the single integer t $1≤t≤10^3)$ — the number of test cases in the test.

Each test case is described by a single string of digits $n$ , which was written out by Polycarp.

The string n contains up to $30$ digits.

Output
Output t integers, each of which is the answer to the corresponding test case, that is how many first digits of the number $π$ Polycarp remembers correctly.

Example
在这里插入图片描述

思路

俗话说得好：“打表出奇迹！”。本题，我们可以直接用一个字符串统计下来圆周率的前三十位——从网上扒下来就行~~~因为，题目简单，不过多累赘~

代码

#include <iostream>using namespace std;string s = "31415926535897932384626433832795028841971693993751058209749445923"; //自己懒得数位数，直接多扒了一点inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void write(int x)
{if (x < 0)putchar('-'), x = -x;else if (x / 10 > 0)write(x / 10);putchar(char(x % 10 + '0'));
}int main()
{int t;cin >> t;while (t --){string npt;cin >> npt;bool flg = 1;for (int i = 0; i < npt.size(); i ++)if (npt[i] != s[i]){cout << i << endl;flg = 0;break;}if (flg)cout << npt.size() << endl;}return 0;
}

B题——Taisia and Dice

原题

Taisia has n six-sided dice. Each face of the die is marked with a number from 1 to 6, each number from 1 to 6 is used once.

Taisia rolls all n dice at the same time and gets a sequence of values $a_{1},a_{2},…,a_{n} (1≤a_{i}≤6)$ , where ai is the value on the upper face of the $i$ -th dice. The sum of this sequence is equal to $s$ .

Suddenly, Taisia’s pet cat steals exactly one dice with maximum value ai and calculates the sum of the values on the remaining $n - 1$ dice, which is equal to $r$ .

You only know the number of dice $n$ and the values of $s, r$ . Restore a possible sequence a that fulfills the constraints.

Input
The first line contains the integer $t (1 \leq t \leq 1000)$ — the number of testcases.

Each testcase is given on a separate line and contains three integers $n, s, r (2 \leq n \leq 50, 1 \leq r < s \leq 300) .$

It is guaranteed that a solution exists.

Output
For each testcase, print: n integers $a_{1},a_{2},…,a_{n}$ in any order. It is guaranteed that such sequence exists.

If there are multiple solutions, print any.

Example
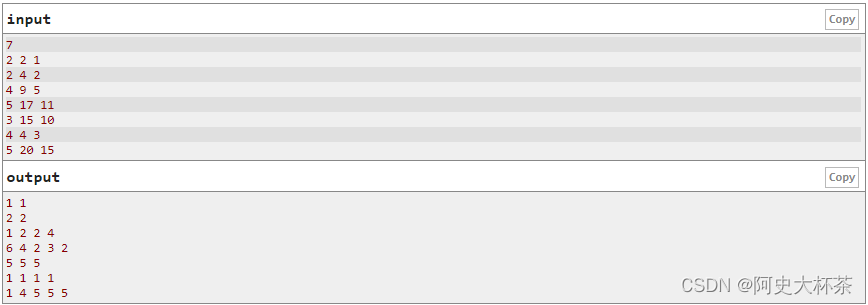
在这里插入图片描述

思路

我们可以算出来最大的数—— $s - r$ ，后面的数就可以随意的构造了~~~当然，我们不能超过最大的数，且所有的数加起来得等于 $s$ ，故我们后面的数可以通过计算算出来，若还有比最大数大的数，通过循环往前匀一下就行了

代码

#include <iostream>using namespace std;const int N = 5e1 + 10;int a[N];inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void write(int x)
{if (x < 0)putchar('-'), x = -x;else if (x / 10 > 0)write(x / 10);putchar(char(x % 10 + '0'));
}int main()
{int t = read();while (t --){int n = read(), s = read(), r = read();a[1] = s - r;int tt = (n - 2 > 0) ? r / (n - 1) : 1;for (int i = 2; i < n; i ++)a[i] = tt;a[n] = r - tt * (n - 2);if (a[n] > a[1]){int c = a[n] - a[1];a[n] = a[n] - c;for (int i = 1; i <= c; i ++)a[i + 1] ++;} for (int i = 1; i <= n; i ++)cout << a[i] << " ";cout << endl;}return 0;
}

C题——Premutation

原题

A sequence of n numbers is called permutation if it contains all integers from 1 to n exactly once. For example, the sequences $[3, 1, 4, 2], [1] an d [2, 1]$ are permutations, but $[1, 2, 1], [0, 1] an d [1, 3, 4]$ — are not.

Kristina had a permutation $p$ of $n$ elements. She wrote it on the whiteboard n times in such a way that:

while writing the permutation at the $i$ -th $(1 \leq i \leq n)$ time she skipped the element $p_{i}$

So, she wrote in total $n$ sequences of length $n - 1$ each.
For example, suppose Kristina had a permutation p = $[4, 2, 1, 3]$ of length $4$ . Then she did the following:

Wrote the sequence $[2, 1, 3]$ , skipping the element $p 1 = 4$ from the original permutation.
Wrote the sequence $[4, 1, 3]$ , skipping the element $p 2 = 2$ from the original permutation.
Wrote the sequence $[4, 2, 3]$ , skipping the element $p 3 = 1$ from the original permutation.
Wrote the sequence $[4, 2, 1]$ , skipping the element $p 4 = 3$ from the original permutation.

You know all $n$ of sequences that have been written on the whiteboard, but you do not know the order in which they were written. They are given in arbitrary order. Reconstruct the original permutation from them.

For example, if you know the sequences $[4, 2, 1], [4, 2, 3], [2, 1, 3], [4, 1, 3]$ , then the original permutation will be $p = [4, 2, 1, 3]$ .

Input
The first line of input data contains a single integer $t (1 \leq t \leq 104)$ — the number of test cases.

The description of the test cases follows.

The first line of each test case contains one integer $n (3 \leq n \leq 100) .$

This is followed by $n$ lines, each containing exactly $n - 1$ integers and describing one of the sequences written out on the whiteboard.

It is guaranteed that all sequences could be obtained from some permutation $p$ , and that the sum $n^2$ over all input sets does not exceed $2⋅10^5$ .

Output
For each test case, output on a separate line a permutation $p$ such that the given $n$ sequences could be obtained from it.

It is guaranteed that the answer exists and it is the only one. In other words, for each test case the required permutation is sure to exist.

Example
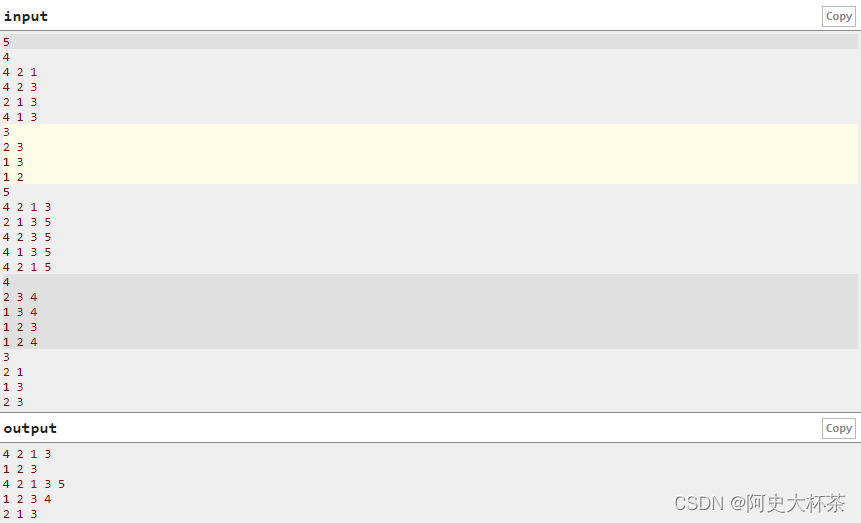
在这里插入图片描述
Note
The first test case is described in the problem statement.

In the second test case, the sequences are written in the correct order.

思路

该题我们可以发现给出的所有序列的第一位只有一个序列是没有开头的数的，所以找到这个序列，将头上的元素补上，就是最初的序列了~~~

代码

#include <iostream>using namespace std;const int N = 1e2 + 10;int a[N][N];inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void write(int x)
{if (x < 0)putchar('-'), x = -x;else if (x / 10 > 0)write(x / 10);putchar(char(x % 10 + '0'));
}int main()
{int t = read();while (t --){int n = read();for (int i = 1; i <= n; i ++)for (int j = 1; j < n; j ++)a[i][j] = read();int ft;for (int i = 1; i < 3; i ++) //找到序列，只用判断前三个就行，因为只有一个序列没有头部元素if (a[i][1] == a[i + 1][1] || a[i][1] == a[i + 2][1]){ft = a[i][1];break;}for (int i = 1; i <= n; i ++){bool flg = 1;if (a[i][1] != ft) //找到了！{cout << ft << " ";  //输出第一个数for (int j = 1; j < n; j ++) //输出后面的数cout << a[i][j] << " ";cout << endl;break;}}	}return 0;
}

D题——Matryoshkas

Matryoshka is a wooden toy in the form of a painted doll, inside which you can put a similar doll of a smaller size.

A set of nesting dolls contains one or more nesting dolls, their sizes are consecutive positive integers. Thus, a set of nesting dolls is described by two numbers: $s$ — the size of a smallest nesting doll in a set and m — the number of dolls in a set. In other words, the set contains sizes of $s, s + 1, \dots, s + m - 1$ for some integer $s$ and $m (s, m > 0)$ .

You had one or more sets of nesting dolls. Recently, you found that someone mixed all your sets in one and recorded a sequence of doll sizes — integers $a_{1},a_{2},…,a_{n}.$

You do not remember how many sets you had, so you want to find the minimum number of sets that you could initially have.

For example, if a given sequence is $a = [2, 2, 3, 4, 3, 1]$ . Initially, there could be $2$ sets:

the first set consisting of $4$ nesting dolls with sizes $[1, 2, 3, 4]$ ;
a second set consisting of $2$ nesting dolls with sizes [2,3].
According to a given sequence of sizes of nesting dolls $a_{1},a_{2},…,a_{n}$ , determine the minimum number of nesting dolls that can make this sequence.

Each set is completely used, so all its nesting dolls are used. Each element of a given sequence must correspond to exactly one doll from some set.

Input
The first line of input data contains $a$ single integer $t (1≤t≤10^4)$ — the number of test cases.

The description of the test cases follows.

The first line of each test case contains one integer $n (1≤n≤2⋅10^5)$ — the total number of matryoshkas that were in all sets.

The second line of each test case contains n integers $a1,a2,…,an (1≤ai≤10^9)$ — the sizes of the matryoshkas.

It is guaranteed that the sum of values of n over all test cases does not exceed $2⋅10^5$ .

Output
For each test case, print one integer $k$ — the minimum possible number of matryoshkas sets.

Example
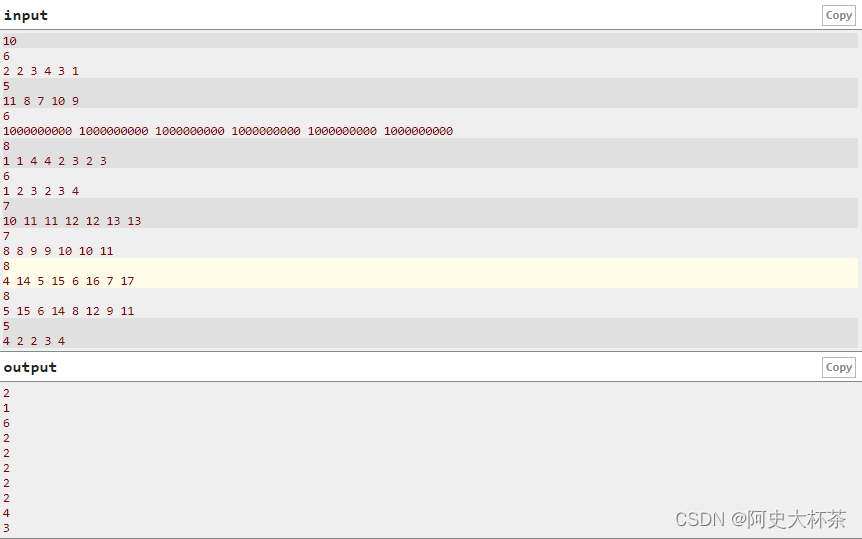
在这里插入图片描述

思路

我们可以先将序列排序，并将所有的大小在其序列中出现的次数统计出来，然后对于最小的，我们肯定是要将集合的数量加上他出的次数的~~~之后，我们枚举每一个，如果和上一个最近的套娃的大小差别不是1，就说明集合的数量要加上当前套娃大小出现的次数，因为他无法套入上一个套娃；反之，若和上一个差别是1就说明可以套上，只需要将集合的数量加上当前套娃大小出现的次数减去上一个套娃大小出现的次数（当然，不能小于0），因为如果当前大小次数多，那么多的部分就无法套到上一个套娃！故，这样就能求出答案了！

代码

#include <bits/stdc++.h>using namespace std;const int N = 2e5 + 10;int T;
int n, cnt, mx;
int a[N];
map<int, int> tmm;inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void write(int x)
{if (x < 0)putchar('-'), x = -x;else if (x / 10 > 0)write(x / 10);putchar(char(x % 10 + '0'));
}int main()
{T = read();while (T --){mx = cnt = 0;tmm.clear();n = read();for (int i = 1; i <= n; i ++)a[i] = read(), tmm[a[i]] ++;sort(a + 1, a + 1 + n);int len = unique(a + 1, a + 1 + n) - a; //去重排序for (int i = 1; i < len; i ++)if (i == 1 || a[i - 1] + 1 != a[i]) //如果套不上cnt += tmm[a[i]]; //加上当前出现的次数else cnt += max(0, tmm[a[i]] - tmm[a[i - 1]]); //加上多出来不能套上的套娃cout << cnt << endl;}return 0;
}

E题——Vlad and a Pair of Numbers

Vlad found two positive numbers $a$ and $b$ ( $a, b > 0$ ). He discovered that $\oplus b = \frac{a + b}{2}$ , where $\oplus$ means the bitwise exclusive OR , and division is performed without rounding…Since it is easier to remember one number than two, Vlad remembered only $a\oplus b$ , let’s denote this number as $x$ . Help him find any suitable $a$ and $b$ or tell him that they do not exist.

Input

The first line of the input data contains the single integer $t$ ( $\le t \le 10^4$ ) — the number of test cases in the test.

Each test case is described by a single integer $x$ ( $\le x \le 2^{29}$ ) — the number that Vlad remembered.

Output
Output $t$ lines, each of which is the answer to the corresponding test case. As the answer, output $a$ and $b$ ( $\le a,b \le 2^{32}$ ), such that $\oplus b = \frac{a + b}{2}$ . If there are several answers, output any of them. If there are no matching pairs, output -1。
Example
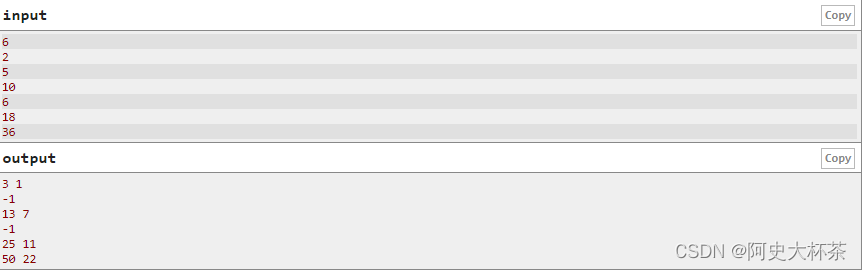
在这里插入图片描述

思路

首先，我们要知道一个公式： $a+b=a\oplus b + a \& b << 1$ 。知道这个公式后，我们就可以推出一个二元式子：
$\begin{cases} \ x = a\& b << 1&\\ \ x = a \oplus b\\ \end{cases}$
之后，不满足情况时有两种情况：

x是奇数
证明： 因为 $\& b << 1$ ，也就是 $\& b \times 2$ ，所以x偶数是满足条件
x二进制不能有连续的1
证明： 因为若x有连续的1，那么a和b就会有两个连续的0，相加之后，不可能凑出x的两个1（如图）

然后，构造a和b也有两种情况：

x的二进制中的当前位置是 $10$ ，那么此时a中取11，b中取01.
证明： $11\oplus 10 = x = 10$ 并且 $11\& 10 << 1 = x = 10$ ，符合二元式子
x的二进制中当前位置是 $0$ ，那么a中取0，b也取0
证明： $0\oplus 0 = x = 0$ 并且 $0\& 0 << 1 = x = 0$ ，也符合二元式子
为什么不能是1,1呢？
这是因为若当前x的位置是0，那么上一个位置一定是0，否则就是第一种情况了~知道上一个位置是0，那么a+b就会进位，故x的上一个位置就变成了1，就不行了

所以，我们就把x的所有情况推了出来，接下来代码实现就很简单了~

代码

#include <iostream>using namespace std;int x, t;
int a, b;inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void write(int x)
{if (x < 0)putchar('-'), x = -x;else if (x / 10 > 0)write(x / 10);putchar(char(x % 10 + '0'));
}int main()
{t = read();while (t --){x = read();if (x & 1 || x & (x >> 1)){cout << -1 << endl;continue;}a = b = 0;for (int i = 0; i <= 33; i ++)if (((x >> (i + 1) & 1) == 1) && ((x >> i & 1) == 0)) //这里要注意，我们虽然是10的情况，但是在二进制下，1是高位，0是低位（同下）a |= 1 << i, a |= 1 << (i + 1), b |= 1 << i; //第一种情况，a取11，b取10cout << a << " " << b << endl;}return 0;
}

F题——Timofey and Black-White Tree

原题

Timofey came to a famous summer school and found a tree on $n$ vertices. A tree is a connected undirected graph without cycles.

Every vertex of this tree, except $c_0$ , is colored white. The vertex $c_0$ is colored black.

Timofey wants to color all the vertices of this tree in black. To do this, he performs $n - 1$ operations. During the $i$ -th operation, he selects the vertex $c_i$ , which is currently white, and paints it black.

Let’s call the positivity of tree the minimum distance between all pairs of different black vertices in it. The distance between the vertices $v$ and $u$ is the number of edges on the path from $v$ to $u$ .

After each operation, Timofey wants to know the positivity of the current tree.

Input

The first line contains the integer $t$ ( $\le t \le 10^4$ ) — the number of testcases.

The first line of each testcase contains the integers $n, c_0$ ( $\le n \le 2 \cdot 10^5$ , $\le c_0 \le n$ ) — the number of vertices in the tree and index of the initial black vertex.

The second line of each testcase contains $n - 1$ unique integers $c_1, c_2, \dots, c_{n-1}$ ( $\le c_i \le n$ , $c_i \ne c_0$ ), where $c_i$ is the vertex which is colored black during the $i$ -th operation.

Each of the next $n - 1$ row of each testcase contains the integers $v_i, u_i$ ( $\le v_i, u_i \le n$ ) — edges in the tree.

It is guaranteed that the sum of $n$ for all testcases does not exceed $\cdot 10^5$ .

Output

For each testcase, print $n - 1$ integer on a separate line.

The integer with index $i$ must be equal to positivity of the tree obtained by the first $i$ operations.

Example
在这里插入图片描述

思路

我们可以用bfs来计算一个黑色的点与他最近的黑色的点的距离。我们可以用一个黑色点来更新其余的点到他的最短距离。例如：
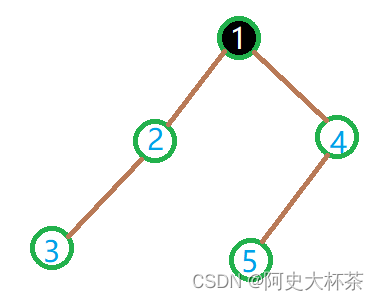
在这里插入图片描述
起初，我们黑色的点是1号，并更新了1号点到所有点的最短距离记入dis，然后假设c数组是 ${1, 2, 3, 4, 5}$ ，我们下面图成黑色的点的点就是2号。

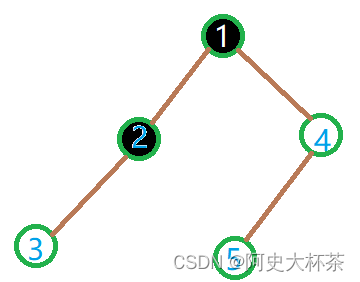
这时，输出刚才更新的dis数组中的dis[2]——1，之后我们再以而为终点更新其余点~~~

…以此类推，最后就能求出所有的

代码

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>using namespace std;const int N = 2e5 + 10;int Data;
int n, c[N], res;
int h[N], e[N * 2], ne[N * 2], idx;
int dis[N];
vector<int> g[N];inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void write(int x)
{if (x < 0)putchar('-'), x = -x;else if (x / 10 > 0)write(x / 10);putchar(char(x % 10 + '0'));
}inline void bfs(int x)
{queue<int> q;q.push(x);dis[x] = 0; //以x为终点更新其他点while (q.size()){int u = q.front();q.pop();for (auto c : g[u])if (dis[u] + 1 < dis[c] && dis[u] + 1 < res) //若距离更小，更新更小值dis[c] = dis[u] + 1, q.push(c);}
}int main()
{memset(h, -1, sizeof h);Data = read();while (Data --){memset(dis, 0x3f, sizeof dis);n = read(), c[0] = read();for (int i = 1; i < n; i ++)c[i] = read(), g[i].clear();g[n].clear();for (int i = 1; i < n; i ++){int u = read(), v = read();g[u].push_back(v);g[v].push_back(u);}res = 0x3f3f3f3f;for (int i = 0; i < n; i ++){res = min(res, dis[c[i]]); //输出当前变黑点距最近黑点的距离bfs(c[i]);if (i > 0)cout << res << " ";}cout << endl;}return 0;
}