LeetCode打卡day49-51 -- 买卖股票系列

知识总结

今天补上了这几天落下的东西, 然后这一篇将概括LeetCode上买卖股票的系列问题, 并且提供了解决该问题的模版.

Leetcode 121. 买卖股票的最佳时机

题目链接

题目说明

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

代码说明

基础版, 股票只能买一次.
方法一:
通过遍历, 记录下遍历的最小股票售价和最大利润, 返回最大利润

class Solution {public int maxProfit(int[] prices) {int minPrice = Integer.MAX_VALUE;int profit = 0;for(int price: prices){minPrice = Math.min(minPrice, price);profit = Math.max(profit, price - minPrice);}return profit;}
}

方法二,
使用动态规划, dp数组的含义:
dp[i][0]: 第i天持有股票的转态下的最大收益
dp[i][1]: 第i天不持有股票的转态下的最大收益
注意: 这里的不持有不是一定指当天卖出, 而是指的一种持续的状态, 可能是当天卖也有可能几天前就卖了

class Solution {public int maxProfit(int[] prices) {//dp[i][0] 第i天持有股票的最大现金//dp[i][1] 第i天不持有股票的最大现金int len = prices.length;int[][] dp = new int[len][2];dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < len; i++){dp[i][0] = Math.max(dp[i-1][0], -prices[i]);//昨天持有, 今天继续持有或者昨天不持有今天买了 因为只能买一次, 所以为0-prices[i]dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]+prices[i]);}// for(int i =0; i < len; i++){//     System.out.println(Arrays.toString(dp[i]));// }       return Math.max(dp[len-1][0], dp[len-1][1]);}
}

Leetcode 122. 买卖股票的最佳时机 II

题目链接

题目说明

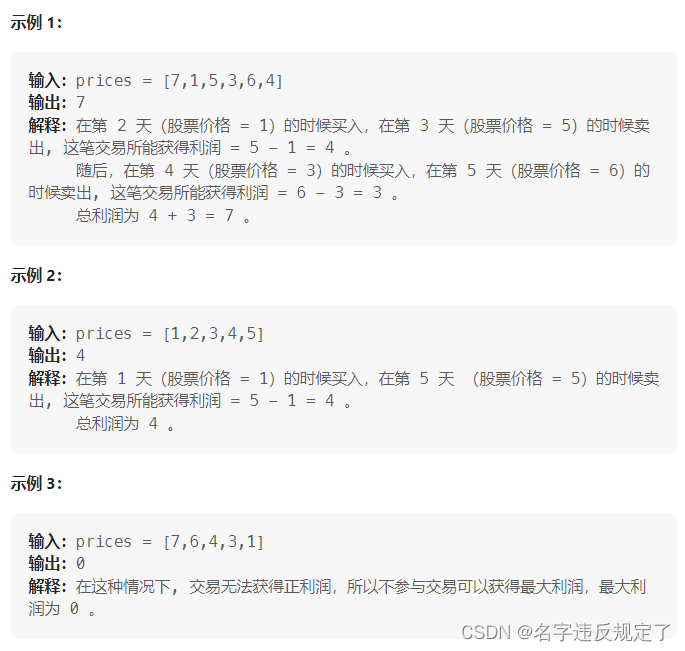
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

代码说明

这题的改变在于不限制购买次数了, 唯一的变化其实就在于持有股票的递推公式变了, 变成了

dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]-prices[i]);

其他的一模一样

public class Solution {public int maxProfit(int[] prices) {int len = prices.length;int[][] dp = new int[len][2];dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < len; i++){dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]-prices[i]);dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]+prices[i]);}return Math.max(dp[len-1][0], dp[len-1][1]);}
}

Leetcode 123. 买卖股票的最佳时机 III

题目链接

题目说明

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）

代码说明

题目说股票限购两次, 但是实际上可以交易0, 1, 2次, 如何做了, 我们可以上面的代码基础上再增加两个状态量即可.

可以认为同一天买进卖出收益为0

class Solution {public int maxProfit(int[] prices) {int len = prices.length;int[][] dp = new int[len][4];dp[0][0] = -prices[0];dp[0][1] = 0;dp[0][2] = -prices[0];dp[0][3] = 0;for(int i = 1; i < len; i++){dp[i][0] = Math.max(dp[i-1][0], 0-prices[i]); //第一次持有dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]+prices[i]); //第一次卖出dp[i][2] = Math.max(dp[i-1][2], dp[i-1][1]-prices[i]); //第二次持有dp[i][3] = Math.max(dp[i-1][3], dp[i-1][2]+prices[i]); //第二次卖出}return dp[len-1][3];}
}

这里提供一种更加快速的方法, 省去了dp数组而是采用四个变量来记录, 方法内核都是一样的

class Solution {public int maxProfit(int[] prices) {if(prices.length == 1) return 0;int buy1 = -prices[0], sell1 = 0, buy2= buy1, sell2 = 0;for(int price: prices){buy1 = Math.max(buy1, -price);sell1 = Math.max(sell1, buy1+price);buy2 = Math.max(buy2, sell1-price);sell2 = Math.max(sell2, buy2+price);} return sell2;}
}

Leetcode 188. 买卖股票的最佳时机 IV

题目链接

题目说明

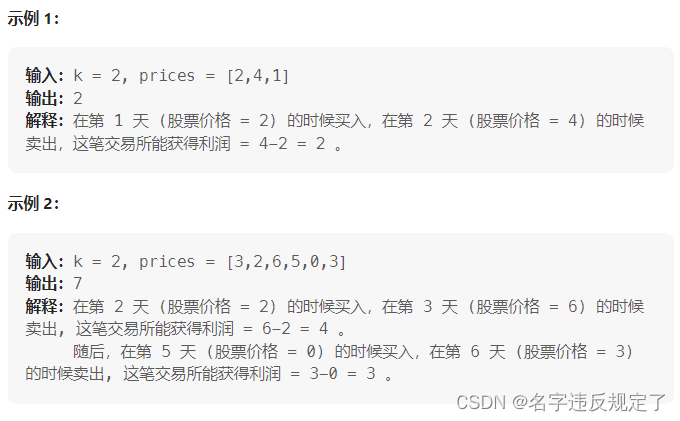
给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格，和一个整型 k 。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

代码说明

这里将难度继续提升, 不是两次而是k次, 如果再傻傻的给dp数组多写维度那也有点傻了. 所以我们借用上一题的优化的方法, dp数组储存的是每个状态的最大值.

class Solution {public int maxProfit(int k, int[] prices) {int[] dp = new int[k*2];for(int i = 0; i <2*k; i+=2){dp[i] = -prices[0];}// System.out.print(Arrays.toString(dp));for(int j = 0; j< prices.length; j++){int price = prices[j];for(int i = 0; i < 2*k; i++){if(i == 0){dp[i] = Math.max(dp[i], -price);}else if(i % 2 == 0){dp[i] = Math.max(dp[i], dp[i-1]-price);}else{dp[i] = Math.max(dp[i], dp[i-1]+price);}}// System.out.print(Arrays.toString(dp));}return dp[2*k-1];}
}

Leetcode 309. 最佳买卖股票时机含冷冻期

题目链接

题目说明

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票)

代码说明

加入了冷冻期, 怎么办?
我们之前都是将股票不持有看做一个状态, 现在拆分一下
第一个是卖出股票那一天的状态:
另外就是卖出股票后保持卖出的状态

class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len <=1) return 0;int[][] dp = new int[len][3];dp[0][0] = -prices[0]; // 持有股的状态dp[0][1] = 0; // 保持卖出股票的状态dp[0][2] = 0; // 卖出股票那一天的状态for(int i = 1; i< len; i++){dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]-prices[i]); //a+2才买入, 有了冷冻期dp[i][1] = Math.max(dp[i-1][1], dp[i-1][2]);//已经卖完了 //a+1dp[i][2] = dp[i-1][0] + prices[i]; // 当天卖股票 a}return Math.max(dp[len-1][1],dp[len-1][2]);}
}

Leetcode 714. 买卖股票的最佳时机含手续费

题目链接

题目说明

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

代码说明

每次交易要付钱了, 那么在把股票卖出去时, 就减去一个fee就好了

class Solution {public int maxProfit(int[] prices, int fee) {int len = prices.length;int[][] dp = new int[len][2];dp[0][0] = -prices[0];dp[0][1] = 0;for(int i =1; i < len; i++){dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]-prices[i]);dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]+prices[i]-fee);}return dp[len-1][1];}
}