航迹推演

​ 做机器人底层程序的时候，经常用到航迹推演（Odometry），无论是定位导航还是普通的方向控制。航迹推演中除了对机器人位姿进行估计，另一个很重要的关系是移动机器人前进速度、转向角速度与左轮速度、右轮速度之间的转换。

​ 在机器人局部路径规划算法DWA解析一文中，是在假设已知机器人前进线速度和角速度的情况下，对机器人航迹推演的位姿进行推导了，然而缺少如何通过左右轮速度得到、，因此本文将补上这个空缺。

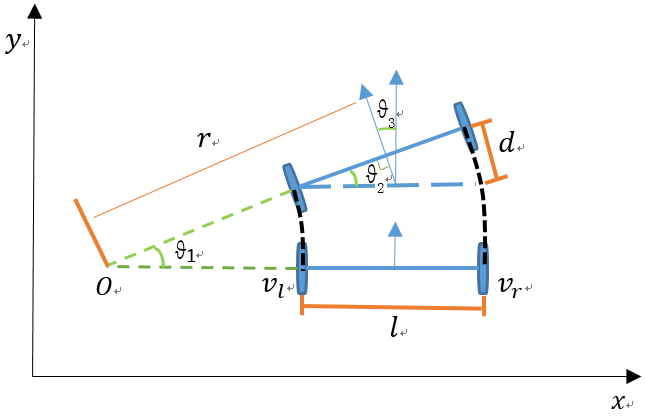
​ 下图是移动机器人在两个相邻时刻的位姿，其中是两相邻时刻移动机器人绕圆弧运动的角度，是两相邻时刻移动机器航向角（朝向角head）的变化量。是左右轮之间的间距，是右轮比左轮多走的距离。是移动机器人圆弧运动的半径。

​ 移动机器人前进速度等于左右轮速度的平均，这个好理解:

$$v=\frac{v_r+v_l}{2}(1)$$
​ 现在来推导机器人航向角如何计算，以及如何计算角速度 。如图所示，把两个时刻的机器人位置叠加在一起，可以清楚的看到移动机器人航向角变化量是 。从图中的几何关系可以得到：
$$\theta_{3} = \theta_{2}=\theta_{1}$$
​ 也就是说移动机器人航向角变化了多少角度，它就绕其运动轨迹的圆心旋转了多少角度。这句话很好验证，我们让机器人做圆周运动，从起点出发绕圆心一圈回到起点处，在这过程中机器人累计的航向角为360度，同时它也确实绕轨迹圆心运动了360度，说明机器人航向角变化多少度，就绕圆心旋转了多少度。而这三个角度中， 很容易计算出来，由于相邻时刻时间很短，角度变化量 很小，有下面的近似公式：
$$\theta_{2}\approx sin\left ( \theta \right )=\frac{d}{l}=\frac{(v_{r}- v_{l})\cdot \Delta t}{l}$$
​ 所以可以得到机器人绕圆心运动的角速度 ，它也是机器人航向角变化的速度：
$$w= \frac{\theta_{1}}{\Delta t}=\frac{v_{r}- v_{l}}{l}(2)$$
​ 线速度、角速度都有了，因此可以推出移动机器人圆弧运动的半径：
$$r = \frac{v}{w}=\frac{l\cdot (v_{r}+v_{l})}{2\left ( v_{r}-v_{l} \right )}(3)$$
​ 从公式（3）可以发现当左轮速度等于右轮速度时，半径无穷大，即直线运动。最后将三个公式综合起来，可以得到左右轮速度和线速度角速度之间的关系如下：
$$v=\frac{v_r + v_l}{2}, \omega=\frac{v_r - v_l}{l}, v=\frac{\omega}{r}=\frac{l(v_r + v_l)}{2(v_r - v_l)}$$