[poj 1151] Atlantis：扫描线+线段树求面积并

本文主要是介绍[poj 1151] Atlantis：扫描线+线段树求面积并，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

想做APIO 2012 Kunai ~~，我要把虐过我的题虐回去~~。把问题转化为了平面中线段的并，或者说面积并。听说这道题要用线段树，大概就是这里了？除了二维线段树，我没有想到什么时间复杂度合理的好方法，而且二维线段树空间会爆。
联想到数轴上的区间覆盖问题，我试着推广，但始终不能抓住要害，把二维的信息压缩到一维。
数轴上的区间覆盖问题至少有两种方法，一是排序之后扫一遍，二是像差分数组一样+1、-1。后者初具扫描线思想的雏形。

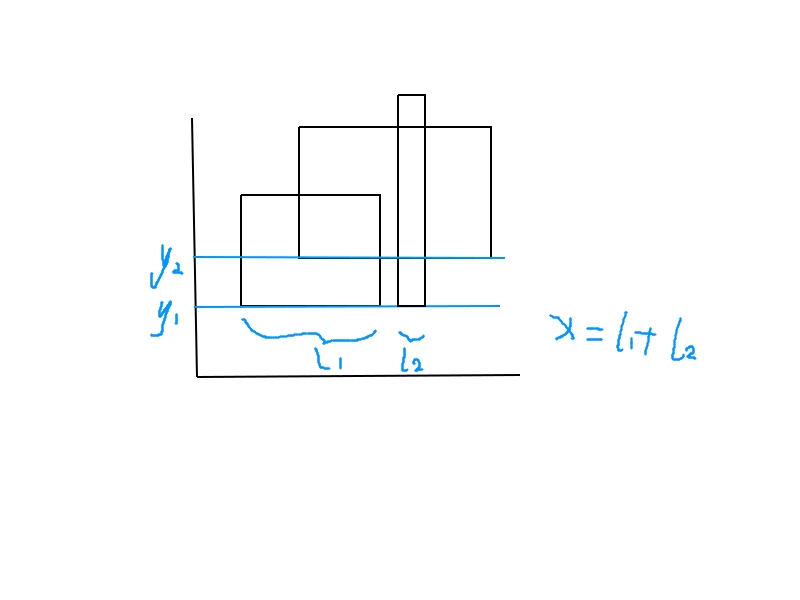
Atlantis一题中，矩形的边都是平行于坐标轴的，这就带来很大的方便。想象一条平行于x轴的直线，从负无穷处徐徐而来，当它扫过两个有矩形的边的相邻位置，设为 $y_1$ 、 $y_2$ ，夹在 $y = y_1$ 和 $y = y_2$ 之间的面积并很容易计算：

S = x (y 2 - y 1)

$S = x(y_2 - y_1)$
其中

x <script id="MathJax-Element-60" type="math/tex">x</script>为夹在两直线间的矩形的宽度之和。我们用线段树维护这个量。

扫描线求面积并

如果扫描线平行于x轴，那么要离散化x坐标。

把每个矩形的上边和下边取出来，按照高度从小到大排序。遍历，如果是下边，那么x坐标对应区间+1，如果是下边，那么x坐标对应区间-1——线段树的区间修改。不同的是，由于+1之后必有-1，标记无须下传，也就是说用不着Lazy Tag。设v是离散化后的区间[l, r]的这个量。如果v > 0，存在一条覆盖整个区间的线段，把离散化映射回去即得长度。如果v = 0，不存在一条线段完整覆盖整个区间，如果[l, r]不是叶子结点，用其子区间来求覆盖的长度，否则长度为0。

这道题PE的人很多啊（我也是）……两组数据之间要加一个空行。

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int MAX_N = 100;
int n, ptr;
double h[MAX_N*2];struct Segment {double l, r, h;int f;bool operator<(const Segment& rhs) const{return h < rhs.h;}
} S[MAX_N*2];struct Node {int v;double w;
} T[MAX_N*8];inline int hash(double x)
{return lower_bound(h, h+ptr, x) - h;
}void update(int o, int l, int r, int L, int R, int a)
{if (L<=l && r<= R)T[o].v += a;else {int m = (l+r)/2;if (L <= m)update(o*2, l, m, L, R, a);if (R > m)update(o*2+1, m+1, r, L, R, a);}T[o].w = T[o].v ? h[r] - h[l-1] : (l == r ? 0 : T[o*2].w + T[o*2+1].w);
}inline void update(const Segment& s)
{update(1, 1, 2*n, hash(s.l)+1, hash(s.r), s.f);
}double solve()
{sort(S, S+2*n);sort(h, h+ptr);ptr = unique(h, h+ptr) - h;double a = 0, &w = T[1].w;update(S[0]);for (int i = 1; i < 2*n; ++i) {a += w * (S[i].h - S[i-1].h);update(S[i]);}return a;
}int main()
{double x1, y1, x2, y2;for (int k = 1; (~scanf("%d", &n)) && n; ++k) {for (int i = 0; i < n; ++i) {scanf("%lf %lf %lf %lf", &x1, &y1, &x2, &y2);S[i*2] = (Segment){x1, x2, y1, 1};S[i*2+1] = (Segment){x1, x2, y2, -1};h[ptr++] = x1;h[ptr++] = x2;  }printf("Test case #%d\nTotal explored area: %.2f\n\n", k, solve());ptr = 0;memset(T, 0, sizeof T);}return 0;
}