本文主要是介绍【VRPTW问题】数学模型与CPLEX求解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、问题描述
1.1 VRP
车辆路径问题(VRP)是指一定数量的客户,各自有不同数量的货物需求,配送中心向客户提供货物,由一个车队负责分送货物,组织适当的行车路线,目标是使得客户的需求得到满足,并能在一定的约束下,达到诸如路程最短、成本最小、耗费时间最少等目的。
1.2 VRPTW
由于VRP问题的持续发展,考虑需求点对于车辆到达的时间有所要求之下,在车辆途程问题之中加入时窗的限制,便成为带时间窗车辆路径问题(VRP with Time Windows, VRPTW)。带时间窗车辆路径问题(VRPTW)是在VRP上加上了客户的被访问的时间窗约束。在VRPTW问题中,除了行驶成本之外, 成本函数还要包括由于早到某个客户而引起的等待时间和客户需要的服务时间。
在VRPTW中,车辆除了要满足VRP问题的限制之外,还必须要满足需求点的时窗限制,而需求点的时窗限制可以分为两种,一种是硬时窗(Hard Time Window),硬时窗要求车辆必须要在时窗内到达,早到必须等待,而迟到则拒收;另一种是软时窗(Soft Time Window),不一定要在时窗内到达,但是在时窗之外到达必须要处罚,以处罚替代等待与拒收是软时窗与硬时窗最大的不同。
二、数学模型
决策变量:两点之间的弧为0,1变量,判断i点是否到达j点
目标函数:成本最低(用距离替代,即距离最短)
约束条件:
- 容量约束
- 时间约束,包括时间窗约束和两点之间前后到达的时间关系约束(防止子回路出现的约束已在其中)
- 每个点只能访问一次的约束(每个点必须被访问)
- 起点约束,必须从起点出发(此处弧为单向)
- 终点约束,必须停在终点(此处弧为单向)
- 客户点不能停留的约束,即进入i点之后必须从i点出去(此处i点为客户点)(与点只能访问一次的约束相辅相成,即可成为每个客户点只能经过一次的约束)


模型解释(个人理解):
wik表示第k辆车到达i点的时刻
约束(2)还表示每个点必须被访问(因为等于1,而不是小于等于1)
约束(6)表示前后到达时间之间的关系,同时消除了子回路(例如,0,1,0的子回路,则会有w0k<w1k<w0k,产生矛盾)
约束(7)表示i点的时间窗约束
约束(8)表示起始点与终点的时间窗约束
三、CPLEX求解
3.1 程序结构
3.1.1 主方法运行
- 记录求解时间
- 读取数据
- 初始化参数
- 测试数据集
- cplex求解与结果打印
- 检验解结果
3.1.2 读取数据
IO流
运用string.split()方法对文本进行切割
3.1.3 初始化参数
总点数、坐标、时间窗、需求量、服务时间数据、距离矩阵、无向图构建
3.1.4 测试数据(可有可无)
判断时间与需求数据是否有误
3.1.5 cplex建模求解
变量不仅仅是决策变量,也还可以是约束中的所需变量
cplex.addLe(a,b)方法指a<=b,注意别写成addLe(b,a)了
3.1.6 检验解结果
测试解的某些数据是否对应算例的数据,该解测试其车辆数、车容量、时间窗是否满满足要求
注意两个整数值转成double值进行比较大小时,有精度误差,需要加上或者减去一定大的小数
3.2 算例(Solomon经典算例C101(100))
VEHICLE
NUMBER CAPACITY10 200CUSTOMER
CUST NO. XCOORD. YCOORD. DEMAND READY TIME DUE DATE SERVICE TIME0 40 50 0 0 1236 0 1 45 68 10 912 967 90 2 45 70 30 825 870 90 3 42 66 10 65 146 90 4 42 68 10 727 782 90 5 42 65 10 15 67 90 6 40 69 20 621 702 90 7 40 66 20 170 225 90 8 38 68 20 255 324 90 9 38 70 10 534 605 90 10 35 66 10 357 410 90 11 35 69 10 448 505 90 12 25 85 20 652 721 90 13 22 75 30 30 92 90 14 22 85 10 567 620 90 15 20 80 40 384 429 90 16 20 85 40 475 528 90 17 18 75 20 99 148 90 18 15 75 20 179 254 90 19 15 80 10 278 345 90 20 30 50 10 10 73 90 21 30 52 20 914 965 90 22 28 52 20 812 883 90 23 28 55 10 732 777 90 24 25 50 10 65 144 90 25 25 52 40 169 224 90 26 25 55 10 622 701 90 27 23 52 10 261 316 90 28 23 55 20 546 593 90 29 20 50 10 358 405 90 30 20 55 10 449 504 90 31 10 35 20 200 237 90 32 10 40 30 31 100 90 33 8 40 40 87 158 90 34 8 45 20 751 816 90 35 5 35 10 283 344 90 36 5 45 10 665 716 90 37 2 40 20 383 434 90 38 0 40 30 479 522 90 39 0 45 20 567 624 90 40 35 30 10 264 321 90 41 35 32 10 166 235 90 42 33 32 20 68 149 90 43 33 35 10 16 80 90 44 32 30 10 359 412 90 45 30 30 10 541 600 90 46 30 32 30 448 509 90 47 30 35 10 1054 1127 90 48 28 30 10 632 693 90 49 28 35 10 1001 1066 90 50 26 32 10 815 880 90 51 25 30 10 725 786 90 52 25 35 10 912 969 90 53 44 5 20 286 347 90 54 42 10 40 186 257 90 55 42 15 10 95 158 90 56 40 5 30 385 436 90 57 40 15 40 35 87 90 58 38 5 30 471 534 90 59 38 15 10 651 740 90 60 35 5 20 562 629 90 61 50 30 10 531 610 90 62 50 35 20 262 317 90 63 50 40 50 171 218 90 64 48 30 10 632 693 90 65 48 40 10 76 129 90 66 47 35 10 826 875 90 67 47 40 10 12 77 90 68 45 30 10 734 777 90 69 45 35 10 916 969 90 70 95 30 30 387 456 90 71 95 35 20 293 360 90 72 53 30 10 450 505 90 73 92 30 10 478 551 90 74 53 35 50 353 412 90 75 45 65 20 997 1068 90 76 90 35 10 203 260 90 77 88 30 10 574 643 90 78 88 35 20 109 170 90 79 87 30 10 668 731 90 80 85 25 10 769 820 90 81 85 35 30 47 124 90 82 75 55 20 369 420 90 83 72 55 10 265 338 90 84 70 58 20 458 523 90 85 68 60 30 555 612 90 86 66 55 10 173 238 90 87 65 55 20 85 144 90 88 65 60 30 645 708 90 89 63 58 10 737 802 90 90 60 55 10 20 84 90 91 60 60 10 836 889 90 92 67 85 20 368 441 90 93 65 85 40 475 518 90 94 65 82 10 285 336 90 95 62 80 30 196 239 90 96 60 80 10 95 156 90 97 60 85 30 561 622 90 98 58 75 20 30 84 90 99 55 80 10 743 820 90 100 55 85 20 647 726 90
3.3 java+cplex源码
package test;import ilog.concert.*;
import ilog.cplex.IloCplex;import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;/*** ClassName: VRPTW* Package: test* Description:CPLEX求解VRPTW问题** @Author:* @Create: 2023/6/11 - 10:48* @Version:*/
public class VRPTW {int locationNum;//总点数double[] locationData;//[x,y,d,a,b,s],坐标+需求+时间窗+服务时间,读取数据用List<double[]> locationList;//存储点数据的集合,读取数据用double[][] location;//存储每个点的坐标[x,y]int[][] arcs;//弧,arcs[i][j]表示i到j点的弧,值为1则此弧存在,值为0则此弧不存在int vehicleNum;//车子总数double[][] distance;//两点之间的距离矩阵,满足三角关系,暂用距离表示花费c[i][j]=distance[i][j]double[] a;//时间窗[ai,bi]double[] b;//时间窗[ai,bi]double E;//仓库点(起始点、终点)时间窗[E,l]double L;//仓库点(起始点、终点)时间窗[E,l]double C;//每辆车子的总容量double[] d;//每个点的需求didouble[] s;//每个点的服务时间List<List<Integer>> routes;//所有车的路径回路集合(用于结果输出)List<List<Double>> arriveTimes;//所有车的路径的时间集合(用于结果的检验)//读取数据public List<double[]> dataInput(String path){File file = null;FileInputStream fileInputStream = null;StringBuilder sb = null;try {file = new File(path);//创建文件对象fileInputStream = new FileInputStream(file);//创建字节输入流对象,导入文件//读入数据int len;sb = new StringBuilder();//创建该对象,将文本内容转为字符串存储到该对象中while ((len = fileInputStream.read()) != -1){sb.append((char)len);//append()方法将一个个(char)len字符存储字符串中}} catch (IOException e) {e.printStackTrace();} finally {try {if (fileInputStream != null) {fileInputStream.close();//关闭数据}} catch (IOException e) {e.printStackTrace();}}//将读取到的数据传到List<double[]> locationList中String[] data = sb.toString().split("\n");//将文本内容按行存储进字符串数组中String[] data1 = data[2].split("\\s+");//将第三行的数据按空格分开,存储进字符串数组中vehicleNum = Integer.parseInt(data1[1]);//车子总数C = Integer.parseInt(data1[2]);//每辆车总容量locationData = new double[6];//数据数组初始化locationList = new ArrayList<>();//数据集合初始化for (int i = 7;i < data.length;i++){//将起始点与100个客户点数据传输到数组和集合里String[] data2 = data[i].split("\\s+");locationData[0] = Double.parseDouble(data2[2]);//坐标xlocationData[1] = Double.parseDouble(data2[3]);//坐标ylocationData[2] = Double.parseDouble(data2[4]);//需求dlocationData[3] = Double.parseDouble(data2[5]);//时间窗alocationData[4] = Double.parseDouble(data2[6]);//时间窗blocationData[5] = Double.parseDouble(data2[7]);//服务时间slocationList.add(locationData.clone());}//将终点传输到数组和集合里,终点数据即起点数据,只是编号不一样而已String[] data2 = data[7].split("\\s+");locationData[0] = Double.parseDouble(data2[2]);//坐标xlocationData[1] = Double.parseDouble(data2[3]);//坐标ylocationData[2] = Double.parseDouble(data2[4]);//需求dlocationData[3] = Double.parseDouble(data2[5]);//时间窗alocationData[4] = Double.parseDouble(data2[6]);//时间窗blocationData[5] = Double.parseDouble(data2[7]);//服务时间slocationList.add(locationData.clone());return locationList;//返回数据集合,包含起点、终点、客户点,共n+2各点}//初始化参数及问题初始条件public void init(){locationNum = locationList.size();//总点数//坐标、时间窗、需求量、服务时间数据location = new double[locationNum][2];//数组初始化a = new double[locationNum];b = new double[locationNum];d = new double[locationNum];s = new double[locationNum];for (int i = 0;i < locationNum;i++){//取数据location[i][0] = locationList.get(i)[0];//x坐标location[i][1] = locationList.get(i)[1];//y坐标a[i] = locationList.get(i)[3];b[i] = locationList.get(i)[4];d[i] = locationList.get(i)[2];s[i] = locationList.get(i)[5];}//仓库点的时间窗,即起点和终点的时间窗E = a[0];L = b[0];//两点之间距离的获取distance = new double[locationNum][locationNum];for (int i = 0;i < locationNum;i++){for (int j = i;j < locationNum;j++){if (i == j){distance[i][j] = Double.MAX_VALUE;//不能自己到达自己,设置距离为无限大} else {//欧式距离distance[i][j] = Math.sqrt(Math.pow(location[i][0] - location[j][0],2) + Math.pow(location[i][1] - location[j][1],2));distance[j][i] = distance[i][j];}}}//三点之间的距离满足三角关系,即a+b<cfor (int k = 0;k < locationNum;k++){for (int i = 0;i < locationNum;i++){for (int j = 0;j < locationNum;j++){if (distance[i][j] > distance[i][k] + distance[k][j]){distance[i][j] = distance[i][k] + distance[k][j];}}}}//G=(V,A)无向图的构建,去除掉某些不符合原始数据条件的弧和规定了起点和终点是单向弧后所得的图arcs = new int[locationNum][locationNum];//无向图中的弧for (int i = 0;i < locationNum;i++){//初始化完全图for (int j = 0;j < locationNum;j++){if (i != j){//其余i==j的弧值默认为0(数组默认值)arcs[i][j] = 1;}}}for (int i = 0;i < locationNum;i++){//除掉某些不符合时间数据和容量数据的弧for (int j = 0;j < locationNum;j++){if (i != j){if (a[i] + s[i] + distance[i][j] > b[j] || d[i] + d[j] > C){arcs[i][j] = 0;}}}}//起点和终点是单向弧,起点只能出不能进,终点只能进不能出for (int i = 0;i < locationNum;i++){arcs[i][0] = 0;arcs[locationNum - 1][i] = 0;}}//测试数据集是否有误public void testData(){for (int i = 0;i < locationNum;i++){for (int j = 0;j < locationNum;j++){if (i != j){if (a[0] + distance[0][i] + s[i] + distance[i][locationNum - 1] > b[locationNum - 1]){//从起始点出发,最早到达i点,再到达终点时,判断其所花费的时间是否满足整个过程的时间窗,不满足则该数据集有误System.out.println("The calculating example is false!");}}}}//最小值min1=最晚到达i点的时间(即时间窗bi) - 起始点到i点所花费的时间(距离),如果min1比整个过程的时间窗E还小,则数据集有误//最小值min2=最早到达i点的时间(即时间窗ai)+ i点的服务时间 + i点到终点所花费的时间(距离),如果min2比整个过程的时间窗L还大,则数据集有误double min1 = Double.MAX_VALUE;double min2 = Double.MAX_VALUE;for (int i = 1;i < locationNum - 1;i++){if (b[i] - distance[0][i] < min1){min1 = b[i] - distance[0][i];}if (a[i] + s[i] + distance[i][locationNum - 1] < min2){min2 = a[i] + s[i] + distance[i][locationNum - 1];}}if (E > min1 || L < min2){System.out.println("Duration false!");System.exit(0);}//如果一个地点的需求量超过一辆车的容量,则数据集有误for (int i = 0;i < locationNum;i++){if (d[i] > C){System.out.println("Demand false!");}}}//CPLEX建模求解public void cplexSolve() throws IloException {//建立模型IloCplex cplex = new IloCplex();//决策变量IloIntVar[][][] x = new IloIntVar[locationNum][locationNum][vehicleNum];//0 1变量,xijk=1时表示第k辆车从i点到j点IloNumVar[][] w = new IloNumVar[locationNum][vehicleNum];//wik表示第k辆车访问i点时的到达时刻for (int i = 0;i < locationNum;i++){for (int j = 0;j < locationNum;j++){if (arcs[i][j] == 0){//弧不存在时,变量即不存在x[i][j] = null;} else {for (int k = 0;k < vehicleNum;k++){//0 1变量x[i][j][k] = cplex.intVar(0,1);}}}for (int k = 0;k < vehicleNum;k++){//定义域定大一些,需大于时间窗Lw[i][k] = cplex.numVar(0,1e15, IloNumVarType.Float,"w" + i + "," + k);}}//目标函数:距离最小值IloLinearNumExpr expr = cplex.linearNumExpr();for (int i = 0;i < locationNum;i++){for (int j = 0;j < locationNum;j++){if (arcs[i][j] == 1){//添加有弧的式子for (int k = 0;k < vehicleNum;k++){expr.addTerm(distance[i][j],x[i][j][k]);}}}}cplex.addMinimize(expr);//约束条件//每个点只能被访问一次for (int i = 1;i < locationNum - 1;i++){IloLinearNumExpr expr1 = cplex.linearNumExpr();for (int j = 1;j < locationNum;j++){if (arcs[i][j] == 1){for (int k = 0;k < vehicleNum;k++){expr1.addTerm(1,x[i][j][k]);}}}cplex.addEq(1,expr1);}//每辆车必须从起始点0开始出发for (int k = 0;k < vehicleNum;k++){IloLinearNumExpr expr2 = cplex.linearNumExpr();for (int j = 1;j < locationNum;j++){if (arcs[0][j] == 1) {expr2.addTerm(1, x[0][j][k]);}}cplex.addEq(1,expr2);}//每辆车必须在终点处停for (int k = 0;k < vehicleNum;k++){IloLinearNumExpr expr3 = cplex.linearNumExpr();for (int i = 0;i < locationNum - 1;i++){if (arcs[i][locationNum - 1] == 1) {expr3.addTerm(1, x[i][locationNum - 1][k]);}}cplex.addEq(1,expr3);}//每辆车到达一个客户点后必须从该客户点出发,不能停留在该客户点(流平衡)for (int k = 0;k < vehicleNum;k++){for (int j = 1;j < locationNum - 1;j++){IloLinearNumExpr expr4 = cplex.linearNumExpr();for (int i = 0;i < locationNum;i++){if (arcs[i][j] == 1){expr4.addTerm(1,x[i][j][k]);}if (arcs[j][i] == 1){expr4.addTerm(-1,x[j][i][k]);}}cplex.addEq(0,expr4);}}//地点到达时间前后关系约束,同时可以用来防止子回路的产生double M = 1e5;//一个足够大但得尽量小的数for (int k = 0;k < vehicleNum;k++){for (int i = 0;i < locationNum;i++){for (int j = 0;j < locationNum;j++){if (arcs[i][j] == 1){IloLinearNumExpr expr5 = cplex.linearNumExpr();expr5.addTerm(1,w[i][k]);expr5.addTerm(-1,w[j][k]);expr5.addTerm(M,x[i][j][k]);cplex.addLe(expr5,M - s[i] - distance[i][j]);}}}}//每辆车到达i点的时刻必须在时间窗之内for (int k = 0;k < vehicleNum;k++){for (int i = 1;i < locationNum - 1;i++){IloLinearNumExpr expr6 = cplex.linearNumExpr();IloLinearNumExpr expr7 = cplex.linearNumExpr();for (int j = 0;j < locationNum;j++){if (arcs[i][j] == 1){expr6.addTerm(a[i],x[i][j][k]);expr7.addTerm(b[i],x[i][j][k]);}}cplex.addLe(expr6,w[i][k]);cplex.addLe(w[i][k],expr7);}}//每辆车从起点0出发和到达终点的时刻必须在整个过程的时间窗[E,L]之内for (int k = 0;k < vehicleNum;k++){IloLinearNumExpr expr8 = cplex.linearNumExpr();IloLinearNumExpr expr9 = cplex.linearNumExpr();expr8.addTerm(1,w[0][k]);expr9.addTerm(1,w[locationNum - 1][k]);cplex.addLe(E,expr8);cplex.addLe(expr8,L);cplex.addLe(E,expr9);cplex.addLe(expr9,L);}//每辆车到达的点的需求量总和不超过车容量for (int k = 0;k < vehicleNum;k++){IloLinearNumExpr expr10 = cplex.linearNumExpr();for (int i = 1;i < locationNum - 1;i++){for (int j = 0;j < locationNum;j++){if (arcs[i][j] == 1){expr10.addTerm(d[i],x[i][j][k]);}}}cplex.addLe(expr10,C);}//求解结果输出cplex.setOut(null);//关闭cplex求解的过程数据routes = new ArrayList<>();//所有车的路径回路集合(用于结果输出)arriveTimes = new ArrayList<>();//所有车的路径的时间集合(用于结果的检验)double obj;//目标函数值for (int k = 0;k < vehicleNum;k++){//初始化上面两个集合List<Integer> route = new ArrayList<>();//一辆车的路径回路链表(可用数组替代)List<Double> arriveTime = new ArrayList<>();//一辆车到达每个地点时的时刻w[i][k]routes.add(route);arriveTimes.add(arriveTime);}//判断建立的数学模型是否有解if (cplex.solve() == false){//模型无解System.out.println("The problem should not solve!!!");return;//若无解,则跳出cplexSolve()方法} else {//模型有解,生成车辆路径for (int k = 0;k < vehicleNum;k++){routes.get(k).add(0);//添加起始点0arriveTimes.get(k).add(0.0);//添加起点到达时刻int i = 0;while (true){for (int j = 0;j < locationNum;j++){if (arcs[i][j] == 1 && cplex.getValue(x[i][j][k]) > 1e-06){routes.get(k).add(j);arriveTimes.get(k).add(cplex.getValue(w[j][k]));i = j;break;}}if (i == locationNum - 1){break;}}}}obj = cplex.getObjValue();//获取目标函数值//打印结果List<Integer> route = new ArrayList<>();System.out.println("最优路径为:");for (int k = 0;k < vehicleNum;k++){route = routes.get(k);System.out.println(route);}System.out.println("最短路径长度为:" + obj);}//检验解的正确性public void checkSolution(){//解的车辆数量是否超过算例数量的判断if (routes.size() > vehicleNum){System.out.println("Error:vehicleNum!!!");System.exit(0);//退出程序}//解中每辆车的车辆载荷是否超过车容量的判断for (int k = 0;k < routes.size();k++){double capacity = 0;List<Integer> route = routes.get(k);for (int i = 0;i < route.size();i++){capacity += d[route.get(i)];}if (capacity > C){System.out.println("error:Capacity!!!");System.exit(0);}}//解中时间窗可行性判断for (int k = 0;k < vehicleNum;k++){List<Integer> route = routes.get(k);List<Double> arriveTime = arriveTimes.get(k);for (int i = 0;i < route.size() - 1;i++){int origin = route.get(i);int destination = route.get(i + 1);double originTime = arriveTime.get(i);double destinationTime = arriveTime.get(i + 1);if (originTime < a[origin] && destinationTime > b[destination]){//到达时间不在时间窗范围内System.out.println("Error:arriveTime!!!");System.exit(0);}if (originTime + s[origin] + distance[origin][destination] > b[destination] + 0.0001){//从i点到j点,到达j点时超过了j点的时间窗System.out.println(origin + "->" + destination);System.out.println("Error:be late");System.exit(0);}if (destinationTime - s[origin] - distance[origin][destination] < a[origin] - 0.0001){//double精度问题,两个整数值相等,换算成double值时不一定相等,容易造成误差,故在两个double值比较大小时,得加或者减去一定大的小数以消除精度差double temp = destinationTime - s[origin] - distance[origin][destination];System.out.println(origin + "->" + destination + ":" + temp);System.out.println("Error:be late!");System.exit(0);}}}}//主方法运行public static void main(String[] args) throws IloException {long startTime = System.currentTimeMillis();//开始时间(毫秒),该时间返回的是long值VRPTW vrptw = new VRPTW();vrptw.dataInput("D:\\IDEA2022\\IDEA projects\\algorithm implementation\\CplexTest\\VRPTWDATAC101(100).txt ");//读取数据,手动修改文件System.out.println("Input successfully!!");System.out.println("cplex求解器求解VRPTW问题:" + vrptw.locationList.size() + "个城市");vrptw.init();//初始化参数vrptw.testData();//测试数据集是否有误vrptw.cplexSolve();//cplex求解及结果输出vrptw.checkSolution();//检查求解结果是否正确System.out.println("程序运行时间:" + (System.currentTimeMillis() - startTime) / 1000d + "s");//所花费的时间,1000d指1000是double值,也就是1000.0}
}
3.4 结果展示
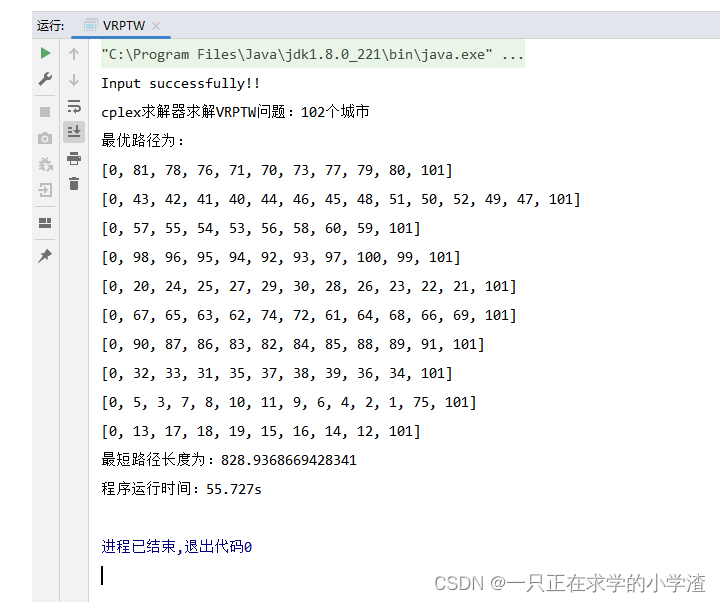
这篇关于【VRPTW问题】数学模型与CPLEX求解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









