DNN for Youtube Recommend System简介

本文主要是介绍DNN for Youtube Recommend System简介，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Abstract

这篇论文主要详细讲述了深度候选生成模型以及描述了一个深度排序模型。同时也提供了practical lessons and insights。

Introduction

YouTube推荐面临三个挑战：

规模：数据规模大，在小数据集上运行好的算法对youtube不适用
更新频率：youtube视频更新频率很高，每秒有小时级别的视频上传，需要在新发布视频和已有存量视频间进行balance。
噪音：用户历史表现总是很稀疏，以及无法观察的外部因素。对用户满意度无法有一个真正的了解，只有一些嘈杂的隐性的反馈信号。视频本身很多数据都是非结构化的。

System overview

整个推荐系统分为candidate generation和ranking两个阶段。在candidate generation阶段相对比较粗糙的召回，在rankin阶段比较精细的计算排序。

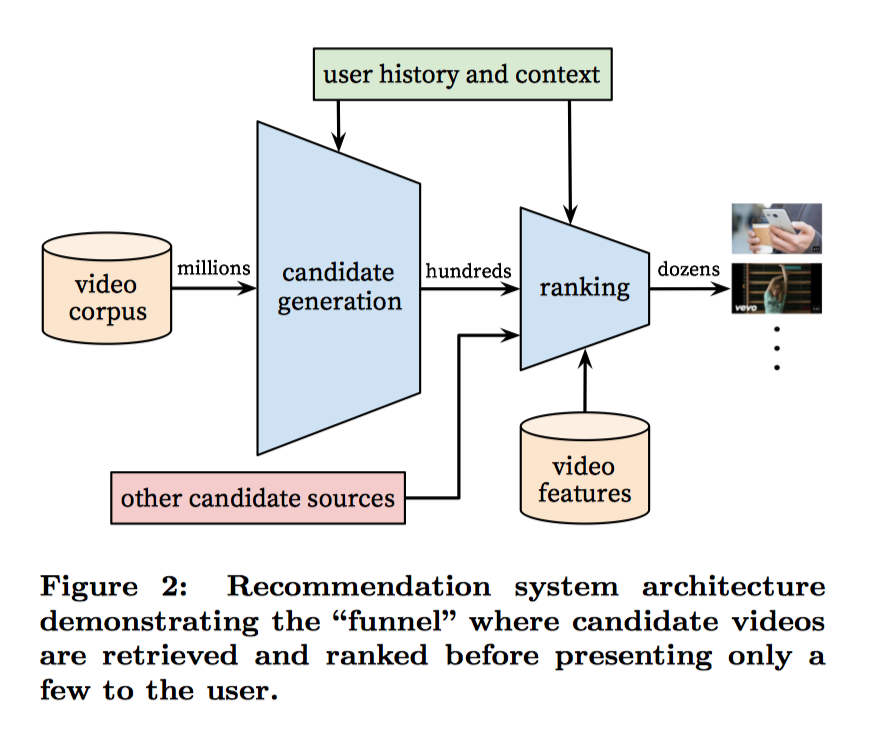
在这里插入图片描述

Recommendation as Classiﬁcation

推荐问题变成了一个大规模的多分类问题。在时刻t，为用户U，上下文context，从视频库V中预测视频i的概率，推荐概率最大的视频。公式如下：

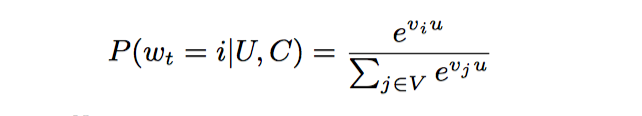
在这里插入图片描述

向量u是用户与上下文的高维embedding，向量j是视频j的embedding向量。DNN的目标就是在用户信息和上下文信息为输入条件下学习用户的embedding向量。

Efﬁcient Extreme Multiclass

为了有效的在这种大规模问题上分类，youtube采用负采样，来提高效率。

Model Architecture

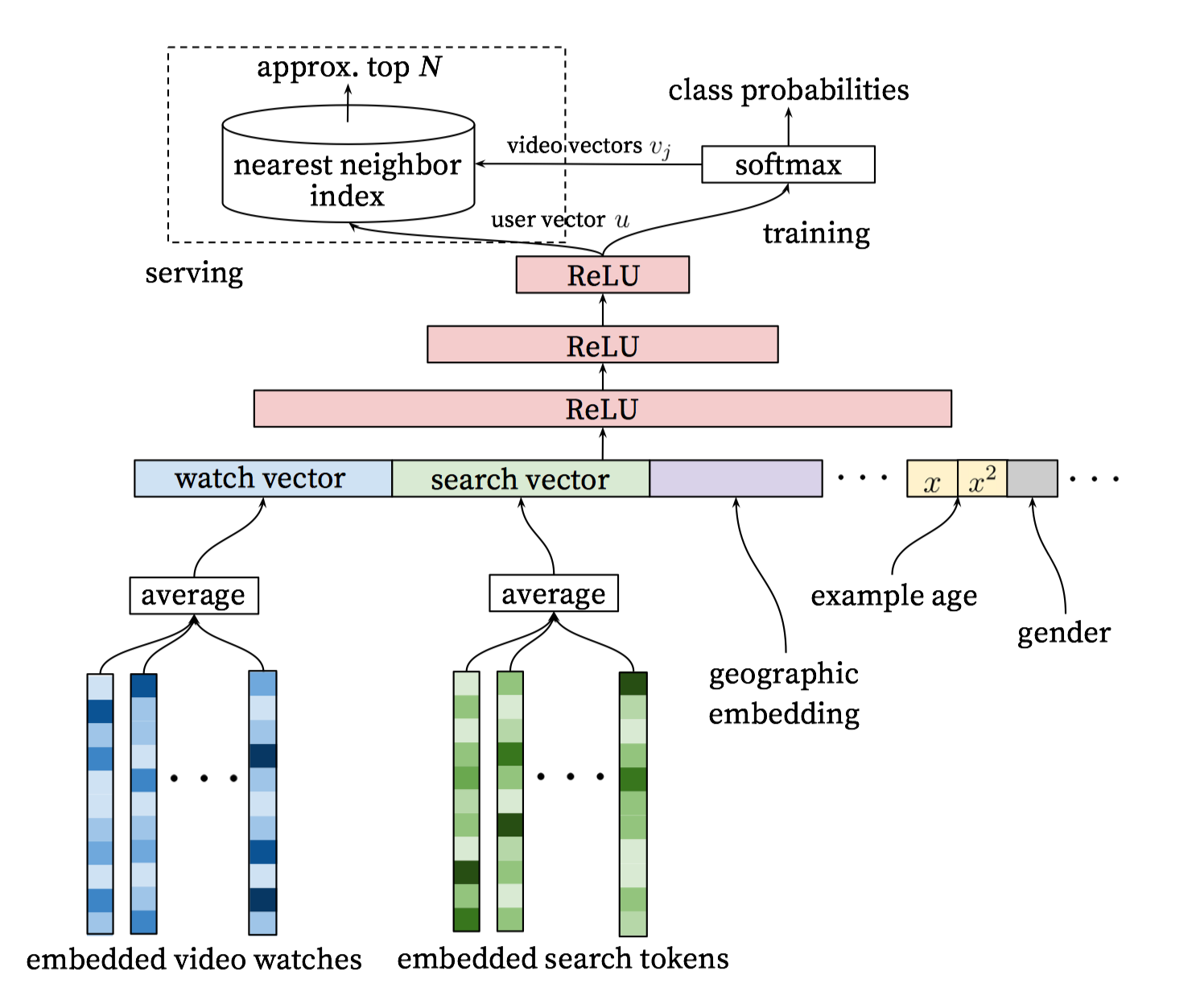
在这里插入图片描述

整个模型架构是包含三层全连接层，使用relu激活函数。输入是用户观看历史、搜索历史、地理位置、example age和其余上下文信息concat成的输入向量；输出分线上和离线训练两个部分。

训练阶段使用softmax输出概率，在服务期间则直接使用接近最近邻搜索来进行生产候选的N个视频。

Heterogeneous Signals

类似于word2vec的做法，每个视频都会被embedding到固定维度的向量中。用户的观看视频历史则是通过变长的视频序列表达，最终通过加权平均（可根据重要性和时间进行加权）得到固定维度的watch vector作为DNN的输入。

引入DNN的好处则是任意的连续特征和离散特征可以很容易添加到模型当中。

主要特征：

搜索历史：搜索历史与观看历史被同等对待，把历史搜索的query分词后的token的embedding向量进行加权平均，能够反映用户的整体搜索历史状态
人口统计学信息：性别、年龄、地域等
其他上下文信息：设备、登录状态等

“Example Age” Feature

虽然用户偏爱新鲜的内容哪怕牺牲相关性。但是youtube也不会因为一个视频是新的所以就推荐给用户。

机器学习系统总是利用历史的例子去预测未来，所以对过去总会有一个隐含的偏差。为了矫正偏差，youtube把训练集的上线时间当作一个特征。下图也充分证明了该方法的有效性。

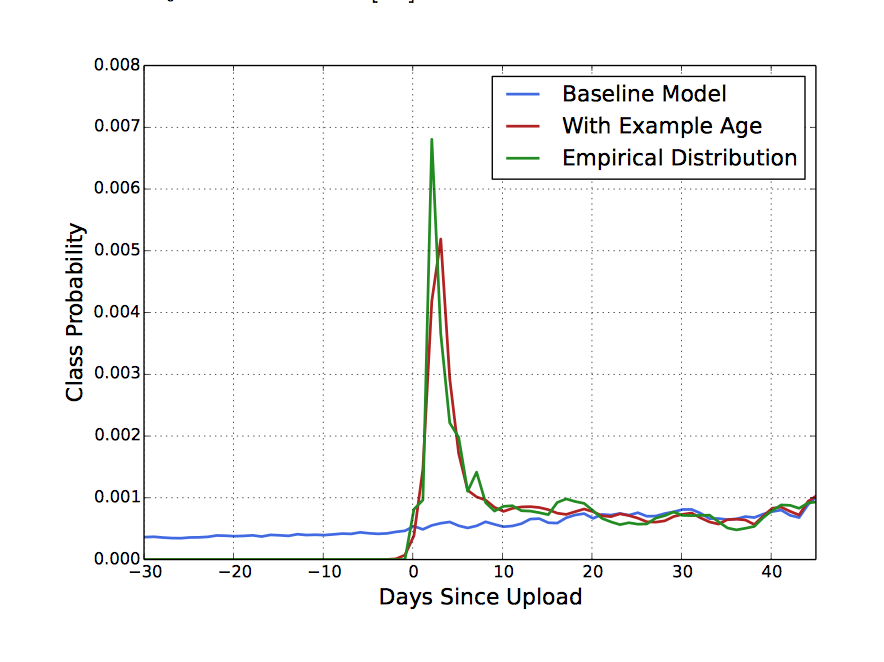
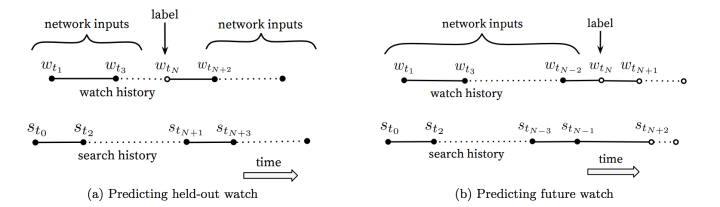
在这里插入图片描述

Label and Context Selection

训练数据被生成来自所有youtube的影片而不是只是我们推荐的影片数据。
每个用户都有固定数量的训练集。
丢弃序列信息以及以一个无序的token袋表达查询请求
asymmetric co-watch：研究发现预测用户的下一个观影数据有更好的表现比从用户历史数据中任意选择效果好。

Ranking

Ranking阶段的最重要任务就是精准的预估用户对视频的喜好程度。在排序阶段面对的数据集比较小，因此会采用更多的特征来计算。
作者在排序阶段所设计的DNN和上文的DNN的结构是类似的，并基于逻辑回归对每一个视频进行独立打分，也就是说，离线训练模块，对视频的打分函数不再是softmax，而是采用的逻辑回归。排序DNN参见下图：

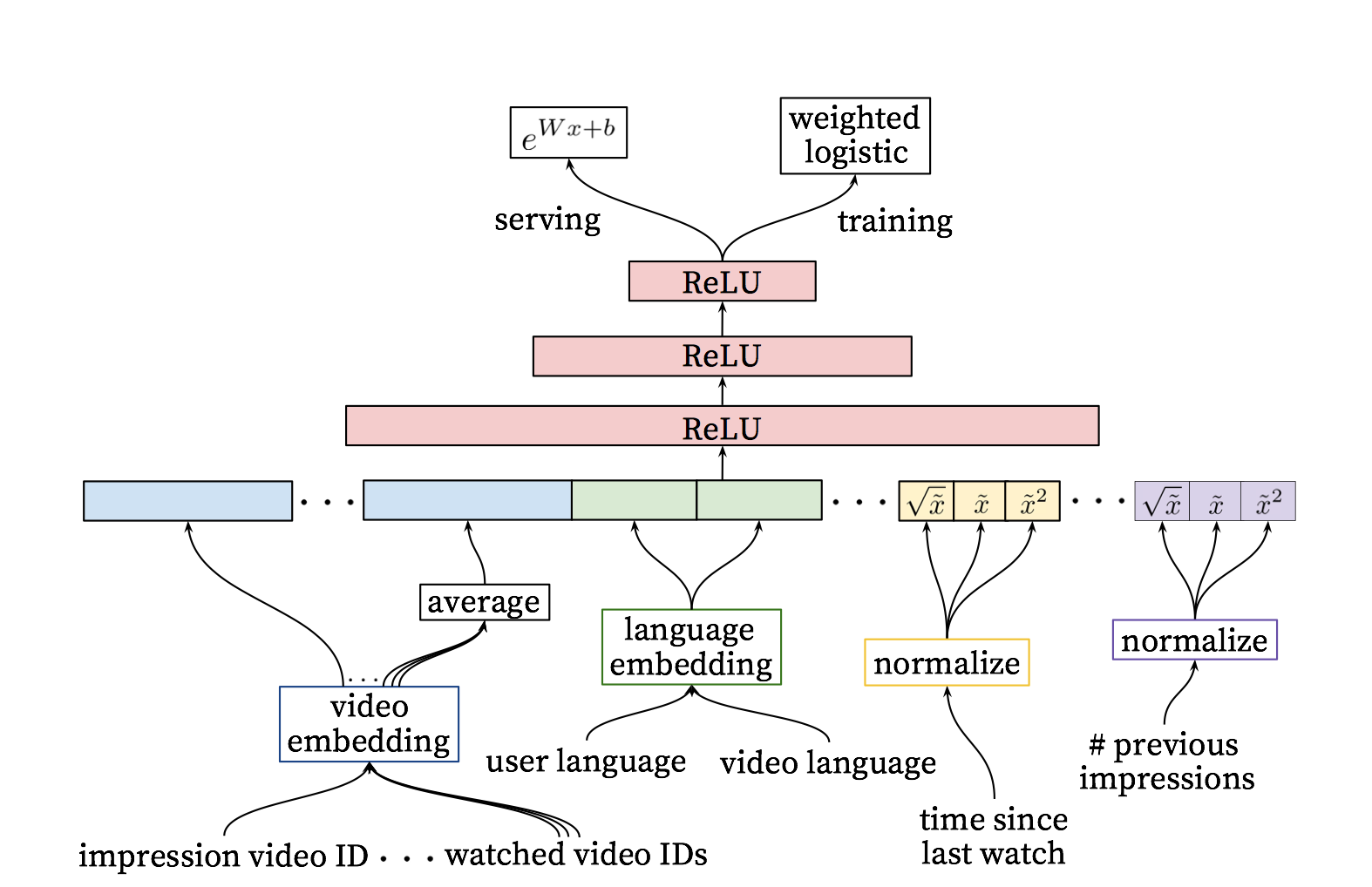
在这里插入图片描述

Feature Engineering

然而在搜索和推荐场景，我们的很难把原始数据直接作为FNN的输入，特征工程仍然很重要。

Embedding Categorical Features

NN更适合处理连续特征，因此稀疏的特别是高基数空间的离散特征需要embedding到稠密的向量中。

Normalizing Continuous Features

一个符合f分布的特征x，等价转化成x~,用微积分使其均匀的分布在[0,1）区间上。

Modeling Expected Watch Time

这个模型是基于交叉熵损失函数的逻辑回归模型训练的。但是我们用观看时长对正样本做了加权，负样本都用单位权重（即不加权）。这样，我们通过逻辑回归学到的优势就是 $\frac{( ∑Ti )}{(N-k)}$ ,其中N是样本数量，k是正样本数量，Ti是观看时长。假设正样本集很小，那么我们学到的优势就近似 $\frac{E[T]}{(1+P)}$ ,P是点击概率，E[T]是观看时间的期望值。因为P很小，那么这个乘积就约等于E[T]。我们用指数函数 $e^x$ 作为最终的激活函数来产生近似观看时长的估计值。