本文主要是介绍简单谐振回路,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、简单谐振回路分析
- 阻抗分析
| 类型 | 并联谐振回路 | 串联谐振回路 |
|---|---|---|
| 示意图 | 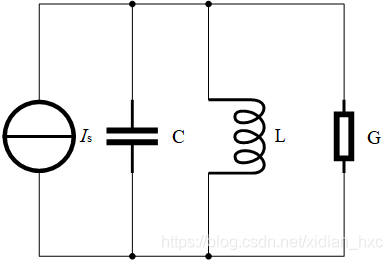 | 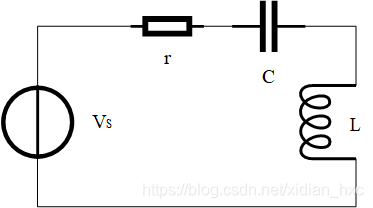 |
| 阻抗与导纳 对 应 的 复 数 相 位 角 度 范 围 : ( − π 2 , π 2 ) _{对应的复数相位角度范围:(-\frac{\pi}{2}, \frac{\pi}{2}) } 对应的复数相位角度范围:(−2π,2π) | Y ( ω ) = G + 1 j ω L + j ω C Y(\omega)=G+\frac{1}{j\omega L}+j\omega C Y(ω)=G+jωL1+jωC | Z ( ω ) = r + j ω L + 1 j ω C Z(\omega)=r+j\omega L+\frac{1}{j\omega C} Z(ω)=r+jωL+jωC1) |
| 谐振角频率 ( 【 阻 抗 / 导 纳 】 虚 部 为 0 ) _{(【阻抗/导纳】虚部为0)} (【阻抗/导纳】虚部为0) | ω o = 1 L C {\omega}_{o}=\frac{1}{\sqrt{LC}} ωo=LC1 | ω o = 1 L C {\omega}_{o}=\frac{1}{\sqrt{LC}} ωo=LC1 |
| 谐振阻抗 | 最大(理想谐振相当于开路) | 最小(理想谐振相当于短路) |
| 品质因数(表征器件损耗) | Q = R / ρ , 其 中 R = 1 / G ; ρ = ω o L 或 ρ = 1 / ω o C Q=R/{\rho},_{其中R=1/G;{\rho}={\omega}_o L或{\rho}=1/{\omega}_o C} Q=R/ρ,其中R=1/G;ρ=ωoL或ρ=1/ωoC | Q = ρ / r Q=\rho/r Q=ρ/r |
两者在理想情况下的交流等效回路在去掉电源后是一致的
- 幅频特性 ( 呈 钟 形 ) _{(呈钟形)} (呈钟形)
| 类型 | 并联谐振回路 | 串联谐振回路 |
|---|---|---|
| 通频带 ( Q ↑ ⟷ B W 3 d B ↓ ) _{(Q\uparrow \longleftrightarrow BW_{3dB}\downarrow)} (Q↑⟷BW3dB↓) | B W 3 d B = f 0 Q BW_{3dB}=\frac{f_0}{Q} BW3dB=Qf0 | B W 3 d B = f 0 Q BW_{3dB}=\frac{f_0}{Q} BW3dB=Qf0 |
| 矩形系数 B W 0.1 / B W 3 d B {BW_{0.1}/BW_{3dB}} BW0.1/BW3dB 3 d B 指 功 率 减 半 幅 值 降 为 最 高 点 的 1 / 2 _{3dB指功率减半幅值降为最高点的1/\sqrt{2}} 3dB指功率减半幅值降为最高点的1/2 | 9.96 | 9.96 |
高选择性 ⇆ \leftrightarrows ⇆宽通频带,无法兼得
- 相频特性(极限分析)
| 类型 | 并联谐振回路(负斜率) | 串联谐振回路(正斜率) |
|---|---|---|
| 失谐状态 ω < ω o _{\omega < \omega_{o}} ω<ωo | 回路呈现感性 | 回路呈现容性 |
| 失谐状态 ω > ω o _{\omega > \omega_{o}} ω>ωo | 回路呈现容性 | 回路呈现感性 |
二、实际谐振回路分析
- 阻抗串并转换

R p = r s ( 1 + Q 2 ) ; X p ( 电 抗 = 感 抗 − 容 抗 ) = X s ( 1 + 1 Q 2 ) R_p=r_s(1+Q^2);\quad {X_p}_{(电抗=感抗-容抗)}=X_s(1+\frac{1}{Q^2}) Rp=rs(1+Q2);Xp(电抗=感抗−容抗)=Xs(1+Q21)
式中 Q = X s / R s = R p / X p Q= X_s/R_s=R_p/X_p Q=Xs/Rs=Rp/Xp;
- 实际并联谐振回路分析(有耗电感 L L L与无耗电容 C C C, r r r为 L L L串联损耗电阻)
谐 振 频 率 : ω p = 1 L C 1 − C r 2 L = ω o 1 − C r 2 L = ω o 1 − 1 Q 0 2 谐振频率:\omega_{p}=\sqrt{\frac{1}{LC}}\sqrt{1-\frac{Cr^2}{L}}=\omega_{o}\sqrt{1-\frac{Cr^2}{L}}=\omega_{o}\sqrt{1-\frac{1}{Q_0^2}} 谐振频率:ωp=LC11−LCr2=ωo1−LCr2=ωo1−Q021
式中 ω o = 1 L C , Q 0 = ω 0 L r \omega_o=\frac{1}{\sqrt{LC}},Q_0=\frac{\omega_0 L}{r} ωo=LC1,Q0=rω0L
- 有载品质因数

1)加入有内阻的 R s R_s Rs电源 I s I_s Is,以及负载 R L R_L RL;
2)图中 R p ≈ r Q 0 2 , L p ≈ L R_p\approx rQ_0^2,L_p \approx L Rp≈rQ02,Lp≈L。
有 载 品 质 因 数 : Q e = R T ρ = Q 0 1 + R p R s + R p R L 有载品质因数:Q_e=\frac{R_T}{\rho}=\frac{Q_0}{1+\frac{R_p}{R_s}+\frac{R_p}{R_L}} 有载品质因数:Qe=ρRT=1+RsRp+RLRpQ0
1) R T = R S ∥ R L ∥ R P R_T=R_S \parallel R_L \parallel R_P RT=RS∥RL∥RP;
2) ρ = ω o L = 1 ω o C \rho =\omega_oL=\frac{1}{\omega_oC} ρ=ωoL=ωoC1。
微信公众号:通信随笔XIDIAN

这篇关于简单谐振回路的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







