leetcode - 319. Bulb Switcher

本文主要是介绍leetcode - 319. Bulb Switcher，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Description

There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.

On the third round, you toggle every third bulb (turning on if it’s off or turning off if it’s on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.

Return the number of bulbs that are on after n rounds.

Example 1:

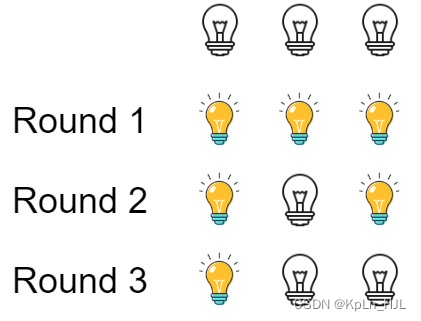
Input: n = 3
Output: 1
Explanation: At first, the three bulbs are [off, off, off].
After the first round, the three bulbs are [on, on, on].
After the second round, the three bulbs are [on, off, on].
After the third round, the three bulbs are [on, off, off]. 
So you should return 1 because there is only one bulb is on.

Example 2:

Input: n = 0
Output: 0

Example 3:

Input: n = 1
Output: 1

Constraints:

0 <= n <= 109

Solution

Solved after others’ solutions…

Ref: https://leetcode.com/problems/bulb-switcher/solutions/77104/math-solution/

A bulb ends up on iff it is switched an odd number of times.

Call them bulb 1 to bulb n. Bulb i is switched in round d if and only if d divides i. So bulb i ends up on if and only if it has an odd number of divisors.

Divisors come in pairs, like i=12 has divisors 1 and 12, 2 and 6, and 3 and 4. Except when i is a square, like 36 has divisors 1 and 36, 2 and 18, 3 and 12, 4 and 9, and double divisor 6. So bulb i ends up on if and only if i is a square.

So just count the square numbers.

Let R = int(sqrt(n)). That’s the root of the largest square in the range [1,n]. And 1 is the smallest root. So you have the roots from 1 to R, that’s R roots. Which correspond to the R squares. So int(sqrt(n)) is the answer.

Time complexity: $o(1)$
Space complexity: $o(1)$

Code

class Solution:def bulbSwitch(self, n: int) -> int:return int(sqrt(n))

这篇关于leetcode - 319. Bulb Switcher的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---