本文主要是介绍智能机器人系统(国防科技大学),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
智能机器人系统–第三章机器人运动控制
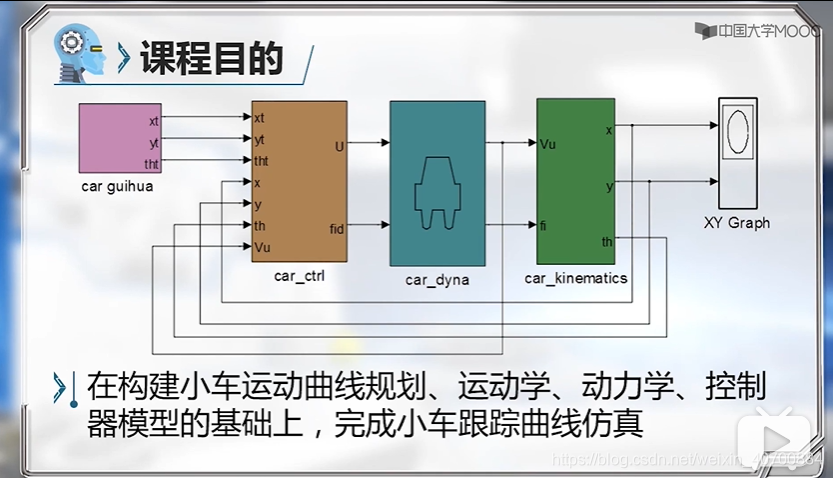

3.1 轮式机器人构型
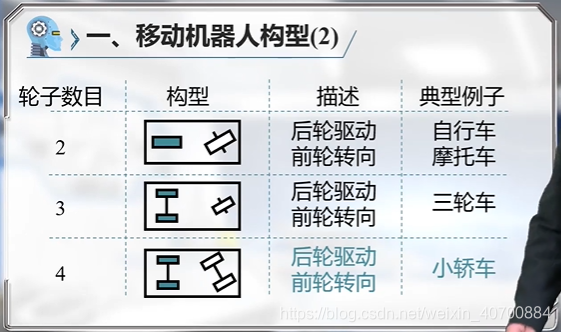
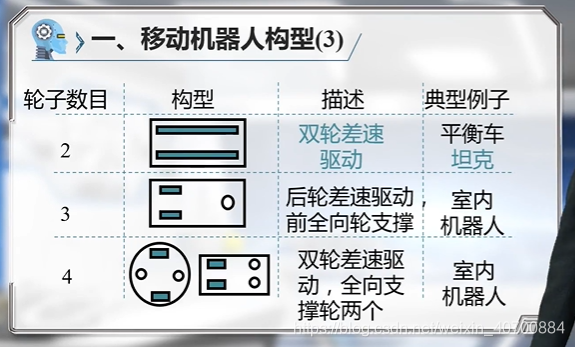
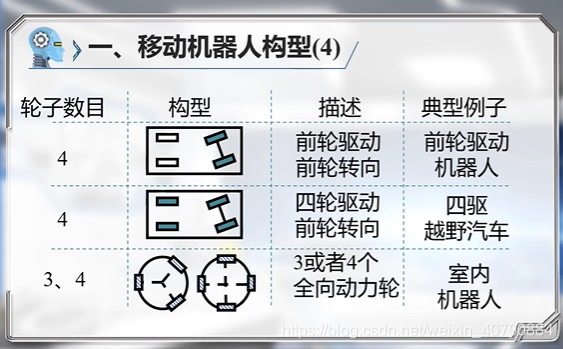

3.2 机器人运动规划—N个控制点的B样条曲线
这个讲解非常详细,一直困惑的三个点:多段的曲线如何保证光滑、如何过指定的点、相邻段的控制点有何关系 终于得到了解答!
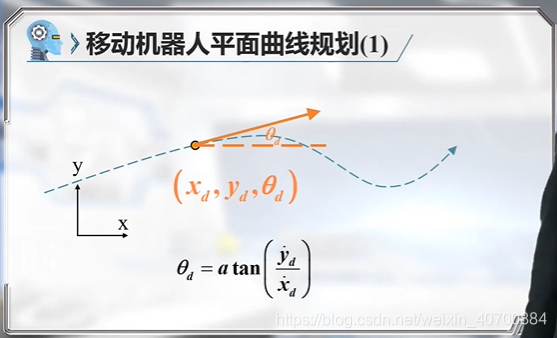

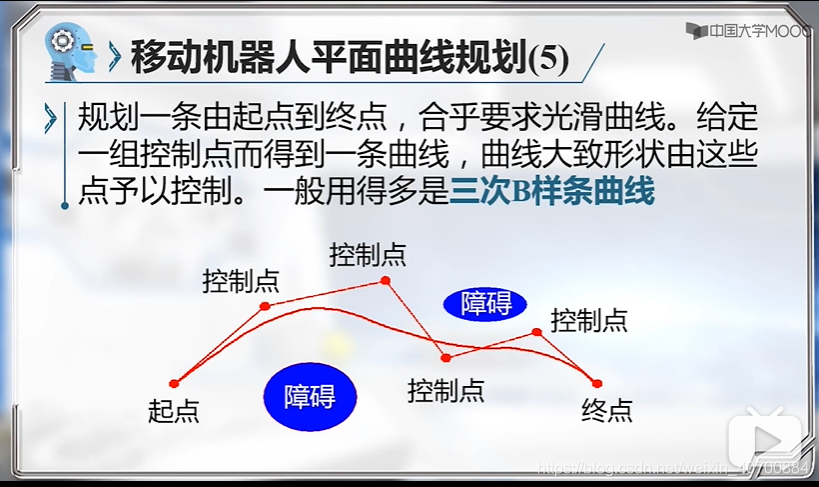

s是规划的路程,0到1表示起点到终点

三阶B样条,有四个控制点,四个样条函数


C1是(0,0),C2是(1,1),C3是(2,1),C4是(3,0)
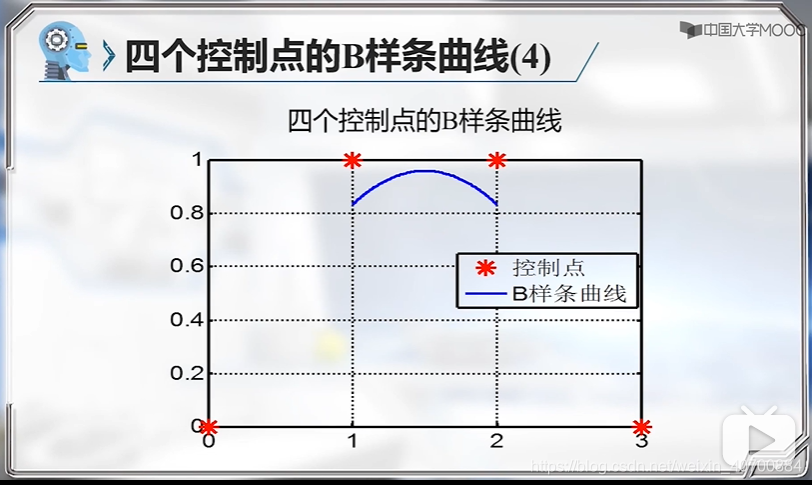
B样条是不过首尾控制点的。

两段B样条的生成:
5个控制点即可生成两段。(关键)

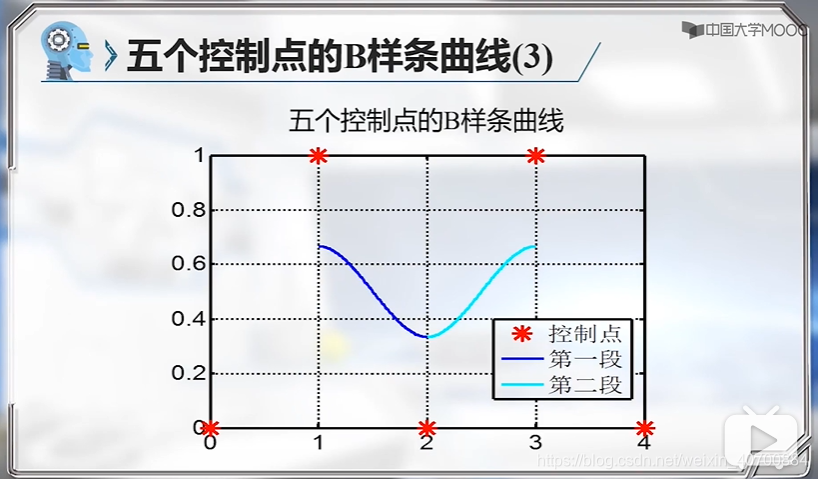


这里其实就是分段三次b样条曲线了,原来是这么实现的!!

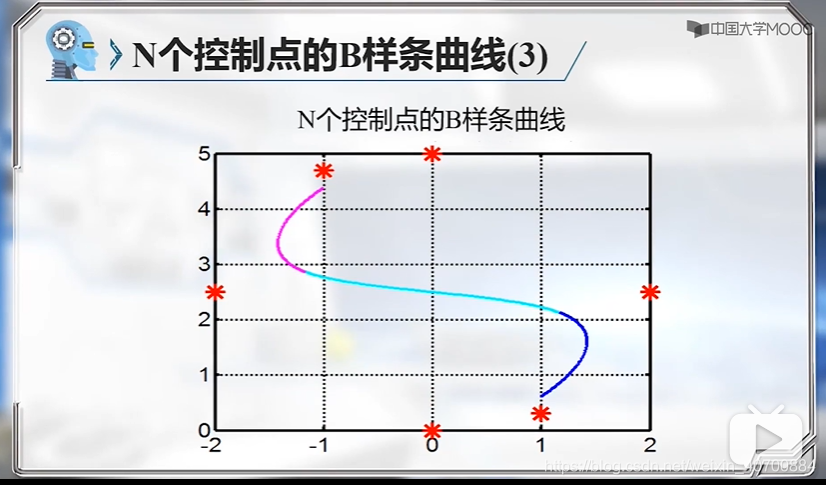
下一步还需要让曲线过起点和终点
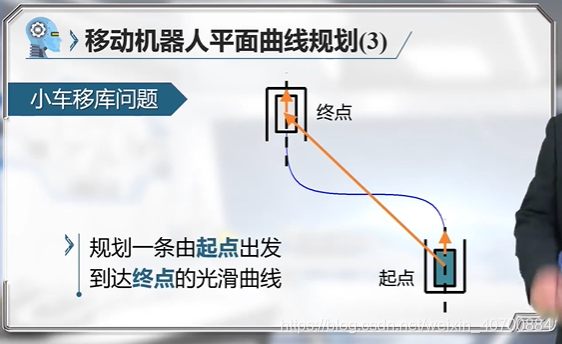
3.3 机器人运动规划—过起点和终点的B样条曲线





V1是起点的速度方向;L是正整数,一般选为小车车长的一般。


带入求解得到:
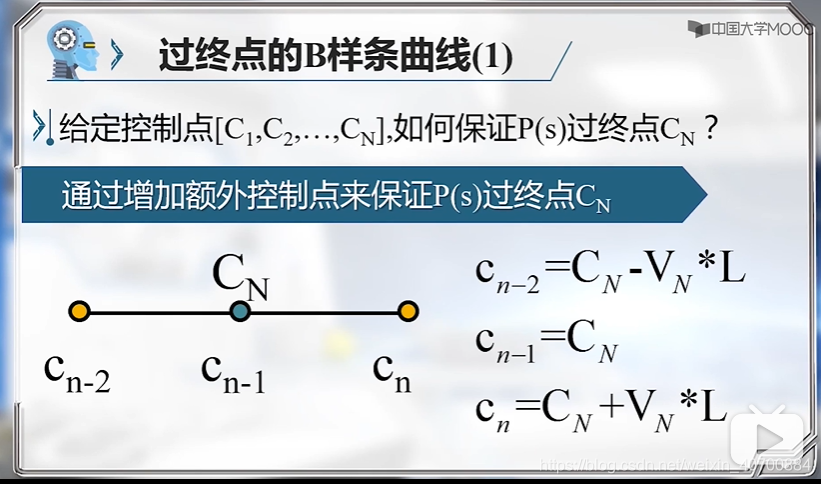
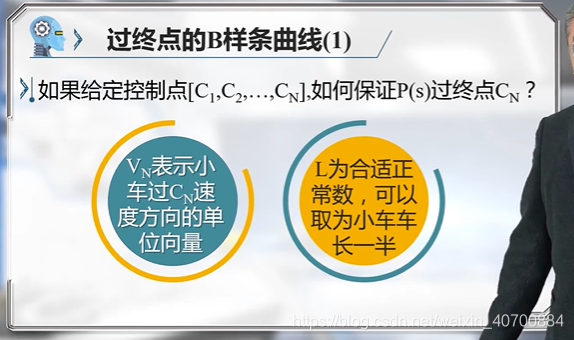







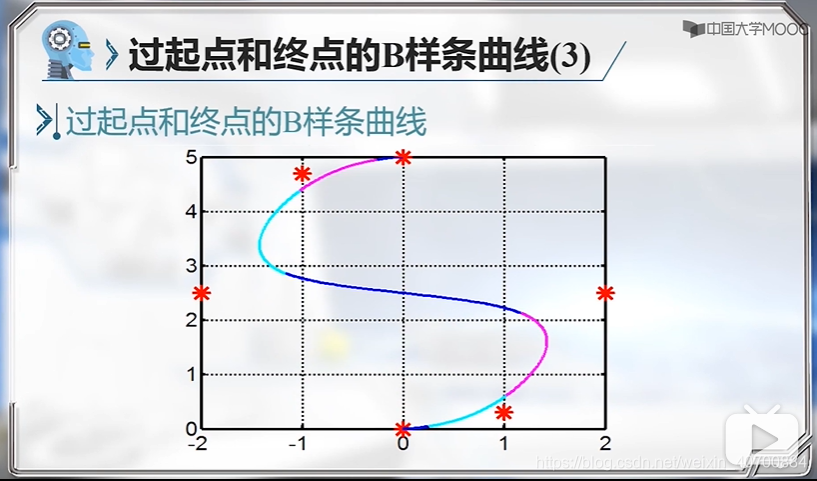

这个性质可以利用一下,可以在中间某个位置,约束一下曲线,比如过圆弧最高点,或者过直线的终点等。
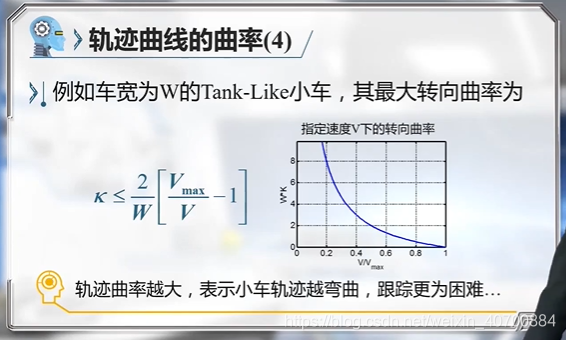
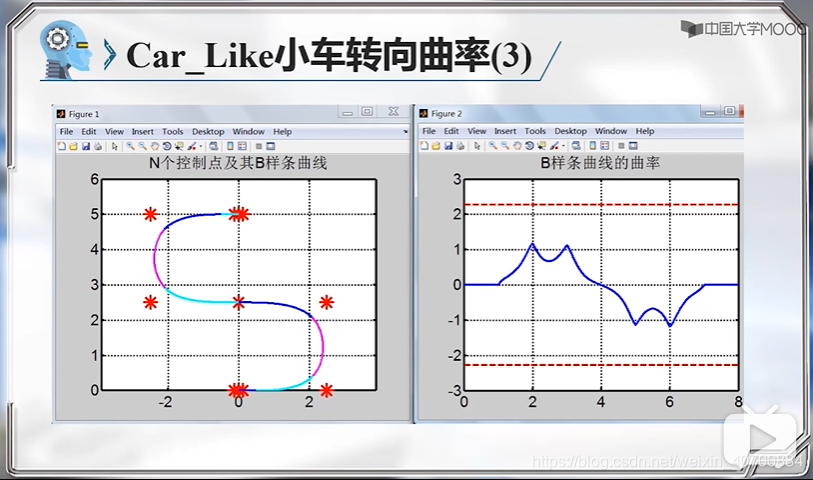
3.4 机器人运动规划—B样条曲线的曲率
B样条如何约束曲率一直不明白,这里终于学到了!

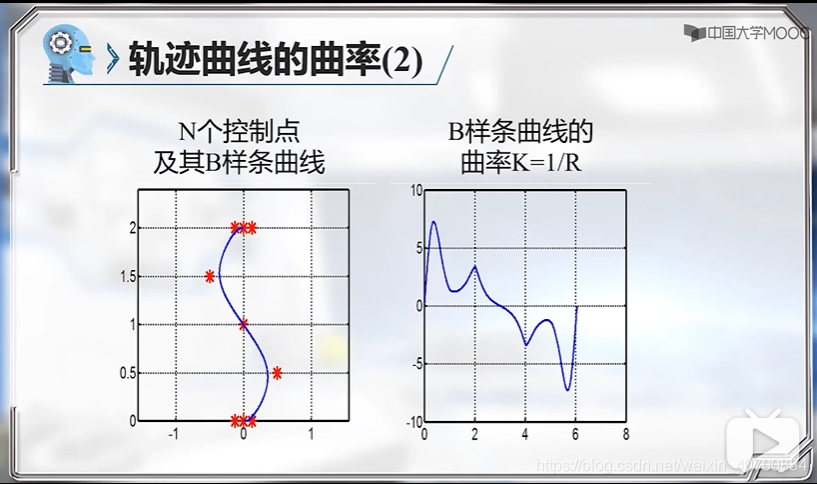




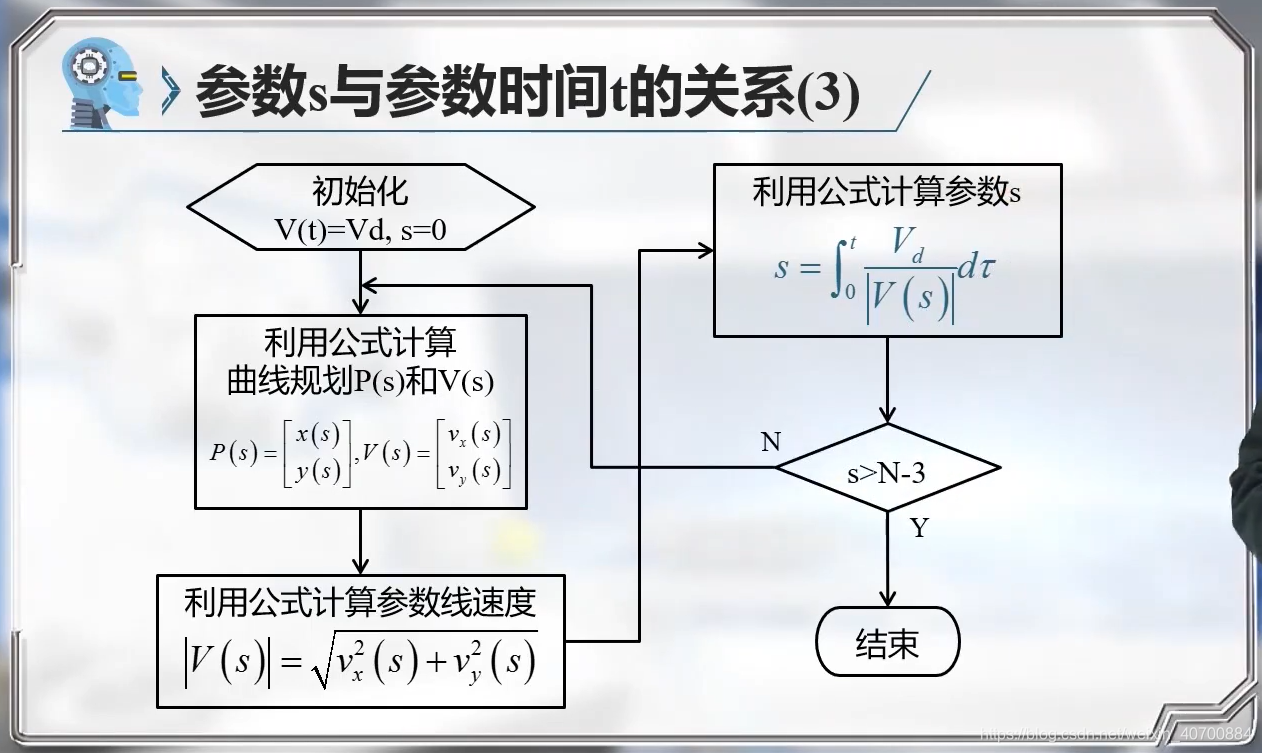
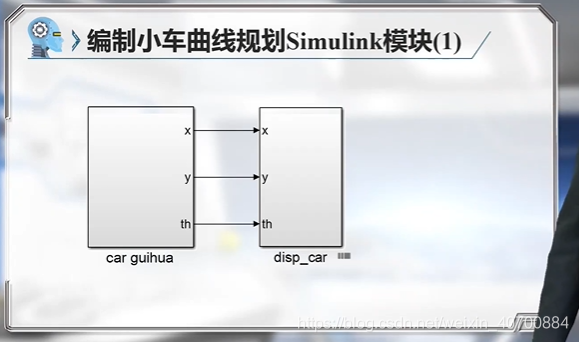
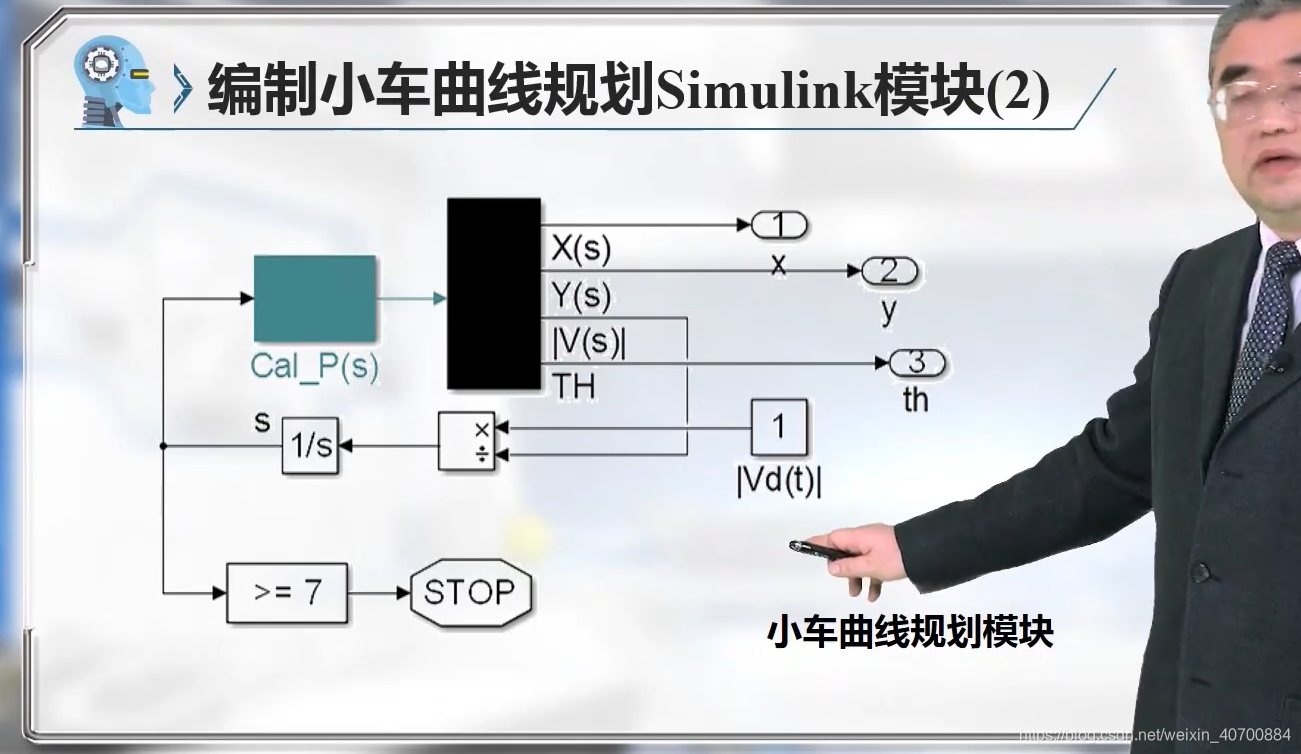
Cal_P(s)模块如下:


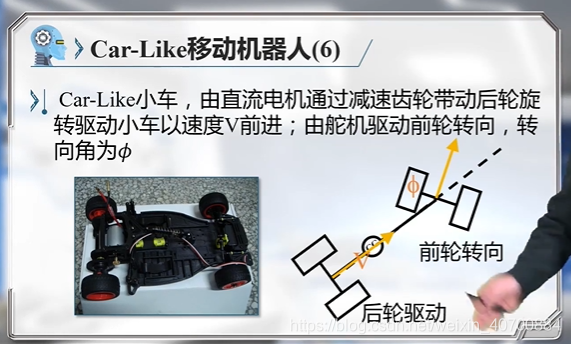
3.5 机器人运动学模型—Car-Like小车运动学模型
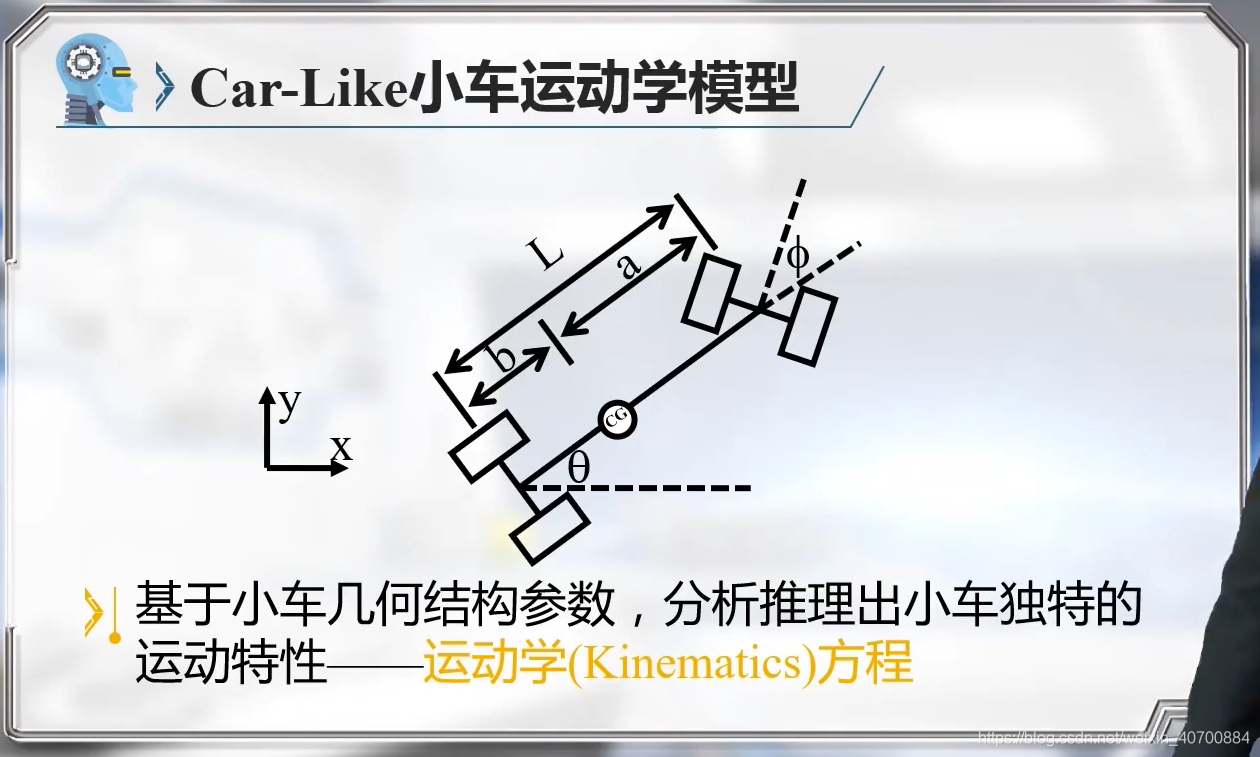
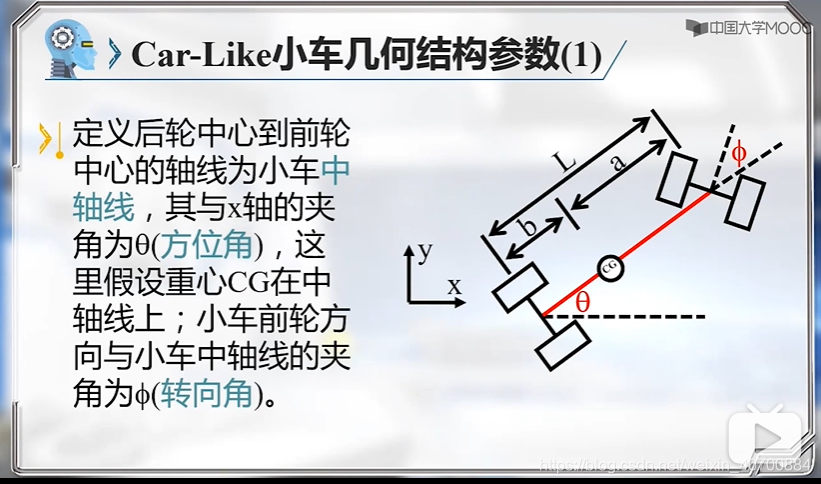
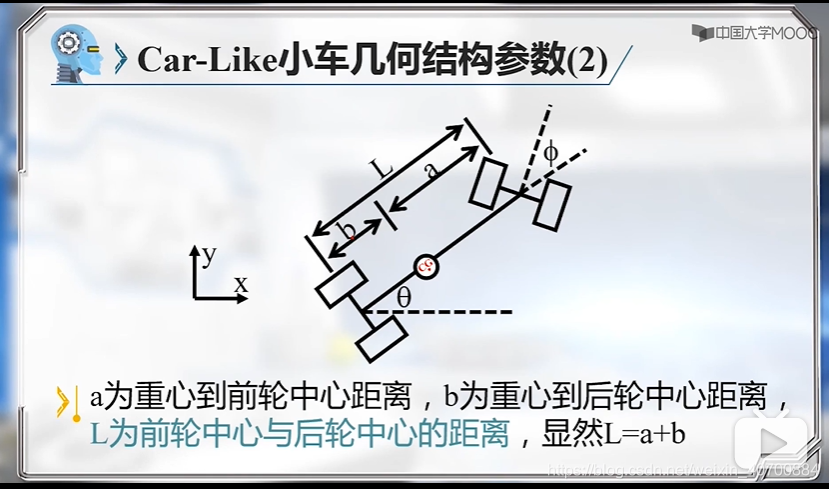
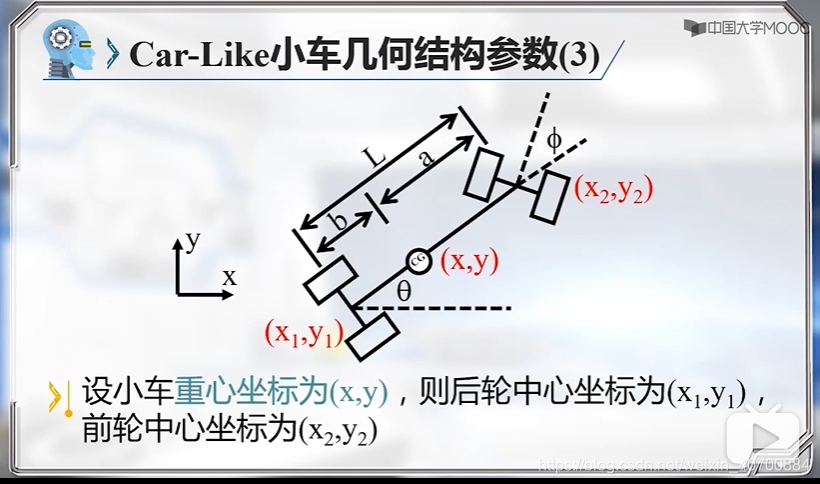




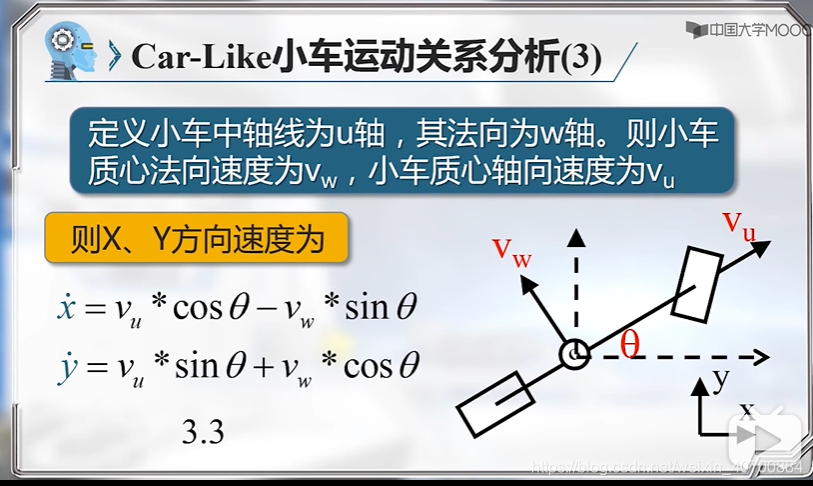



用后轮中心更简单,所以后边就用后轮中心,而不用质心!!


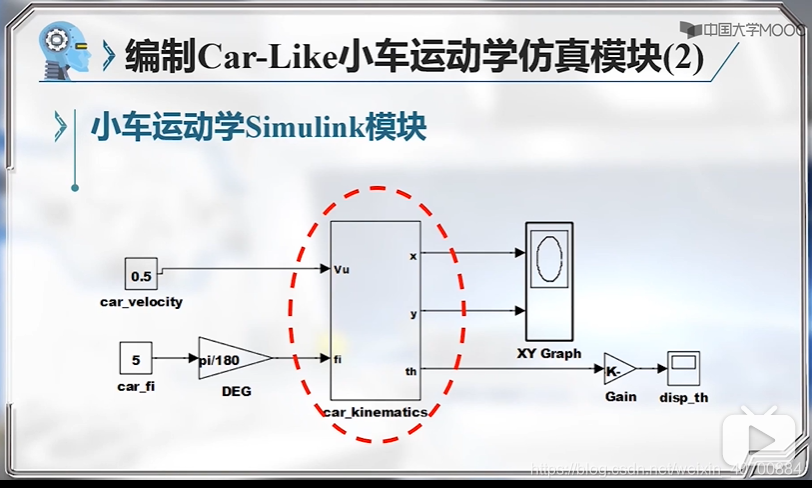
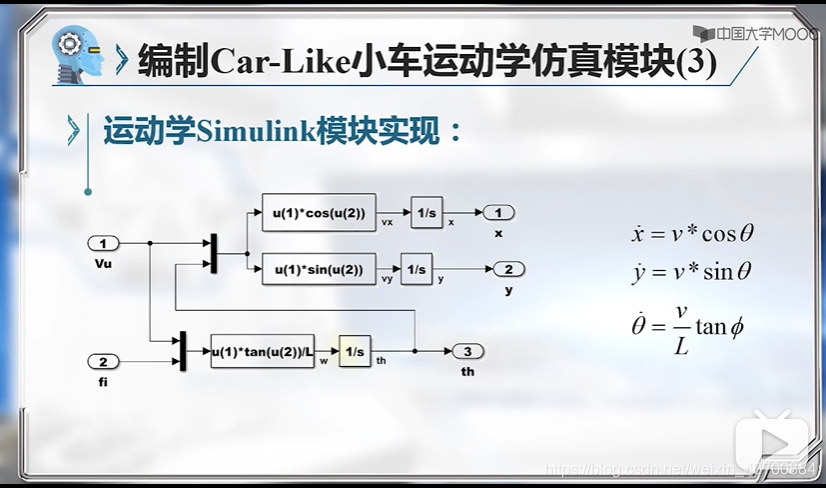




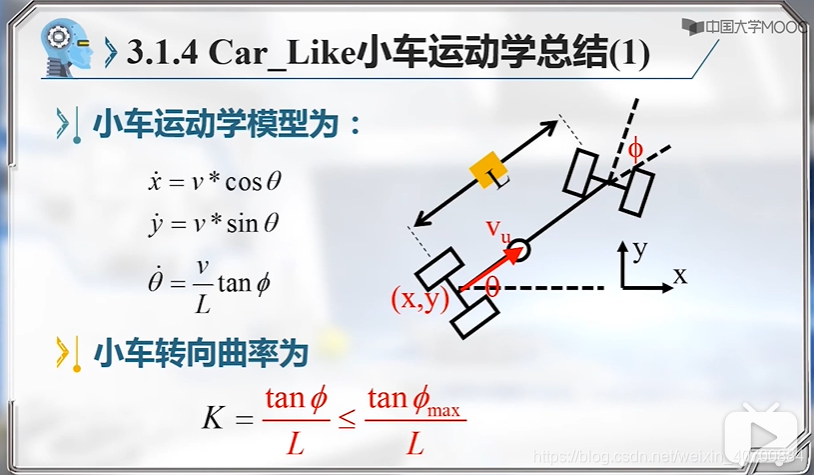
注意,这里是用小车后轮中心建模的。因为后轮的表达式简单,一般用后轮。
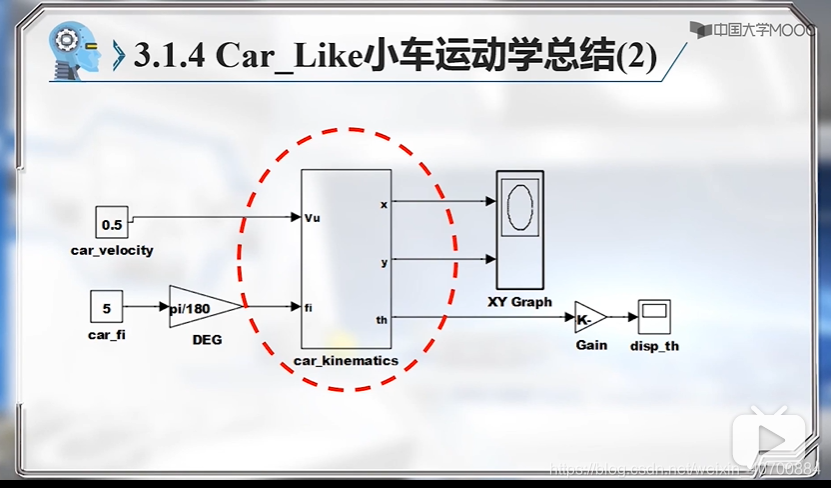

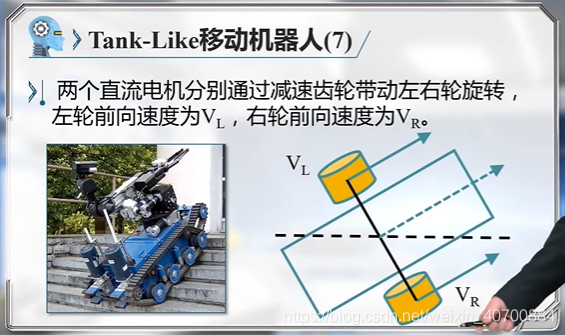
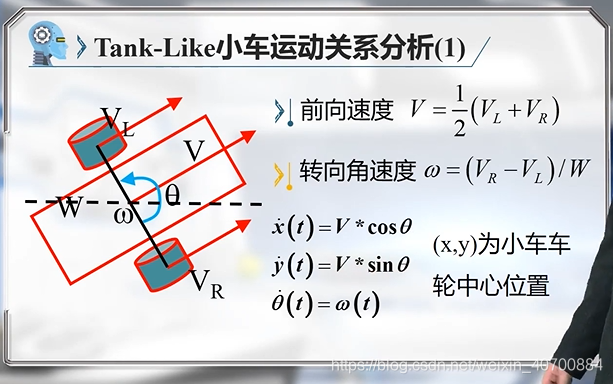
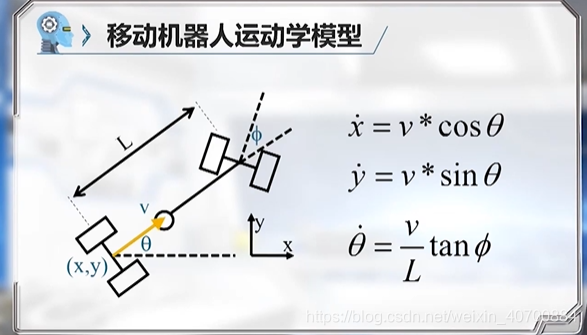
3.6 机器人运动学模型—Tank-Like小车运动学模型
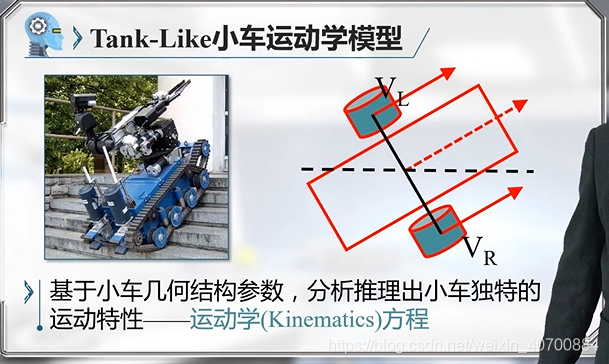
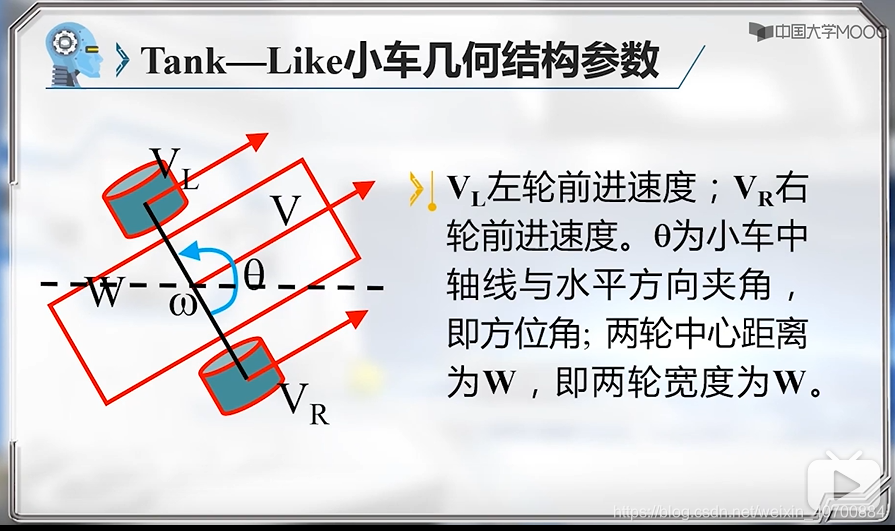
对于car-like,用的是小车后轮中心,对于tank-like用的是车轮中心位置。



当前向速度V为零时,也就是静止,曲率时无限大的。
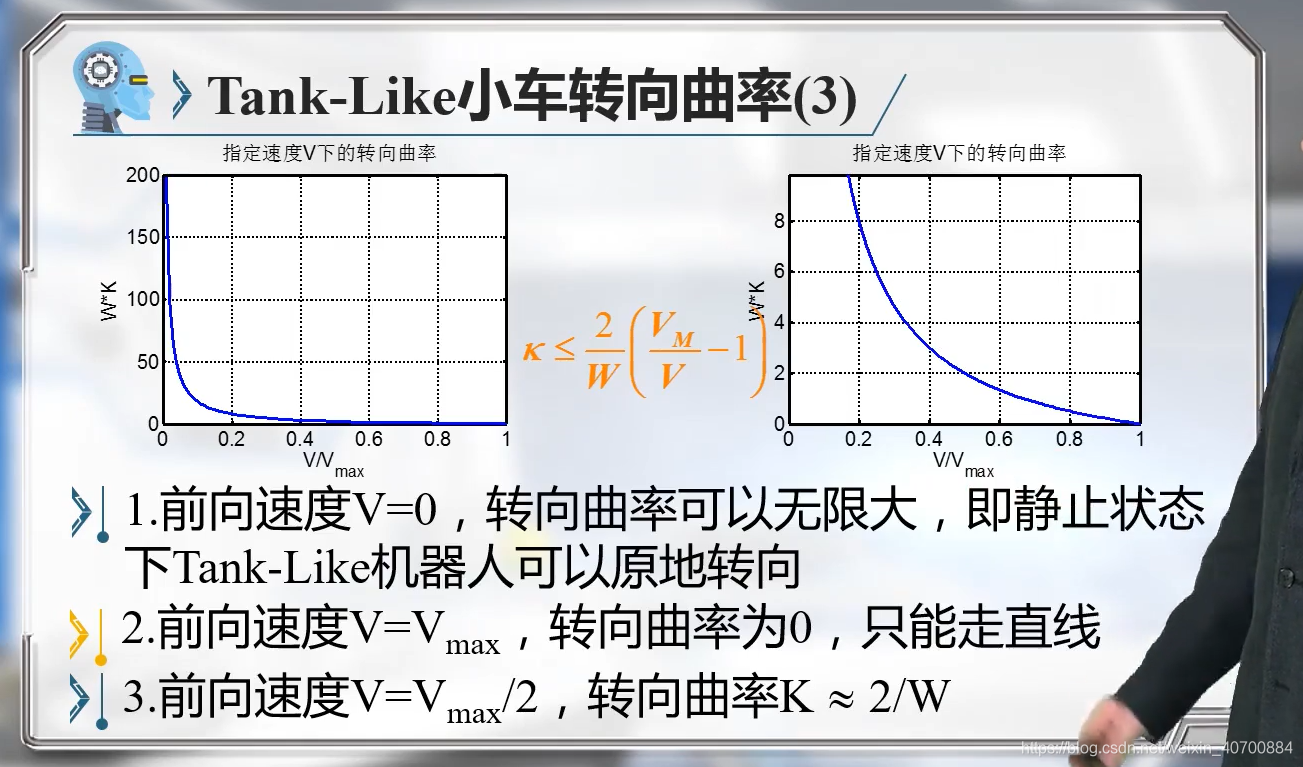
清洗车应该就是这种。一般在前进速度和转向能力之间取个折中的值。
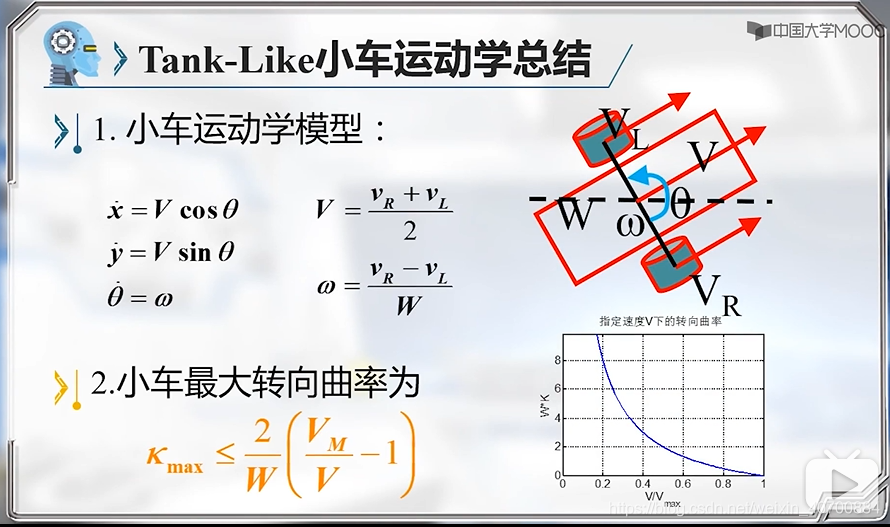
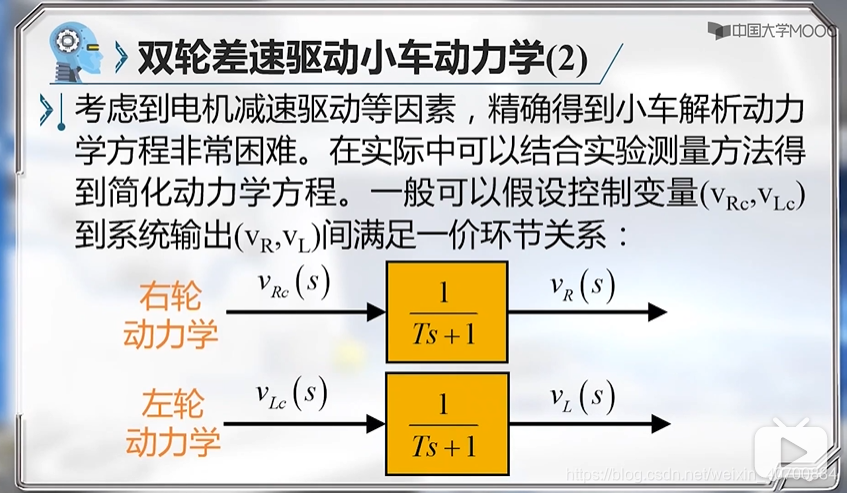
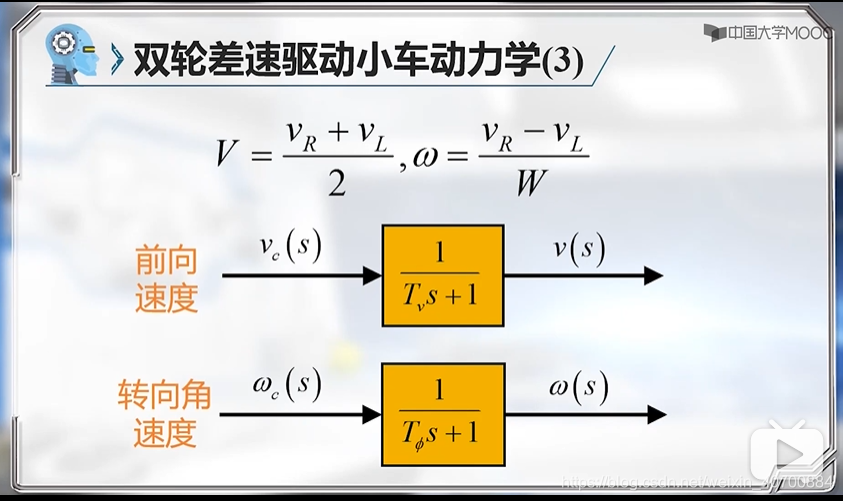
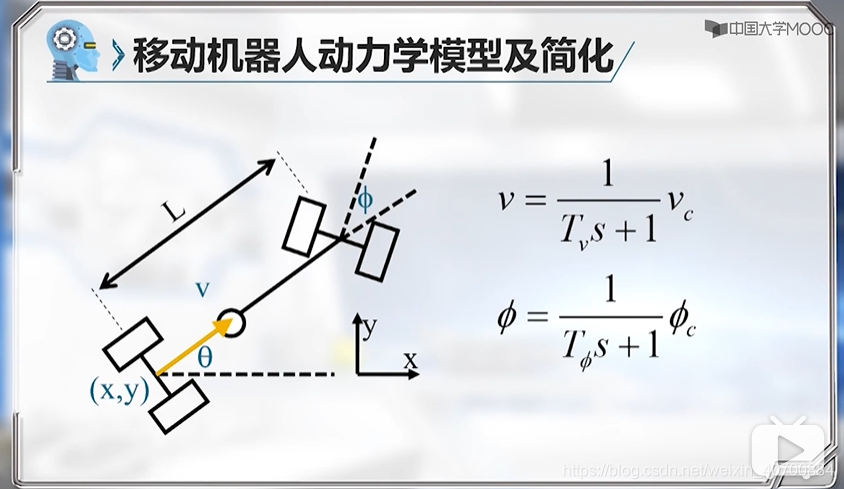
3.7 机器人动力学模型及简化
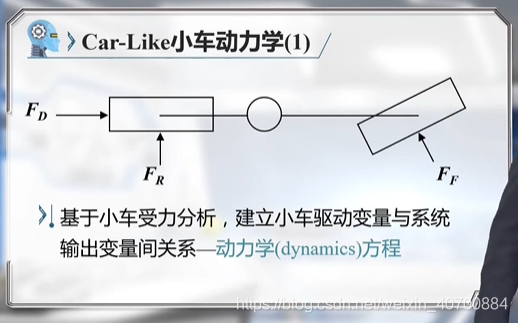
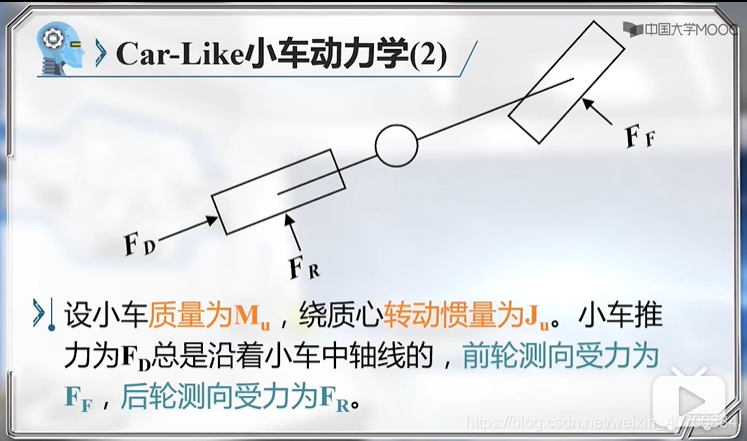
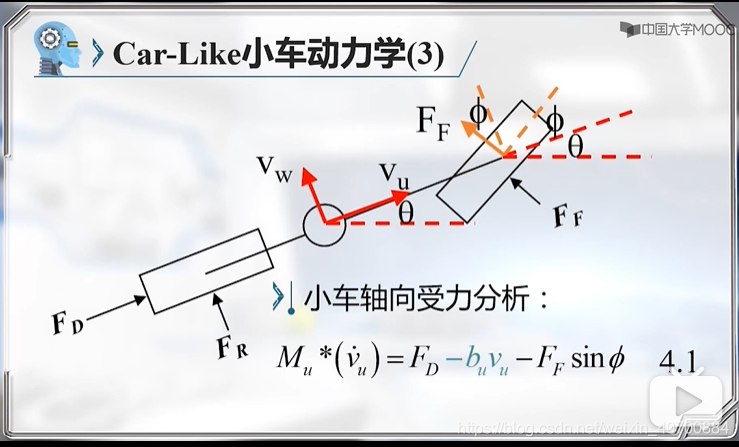
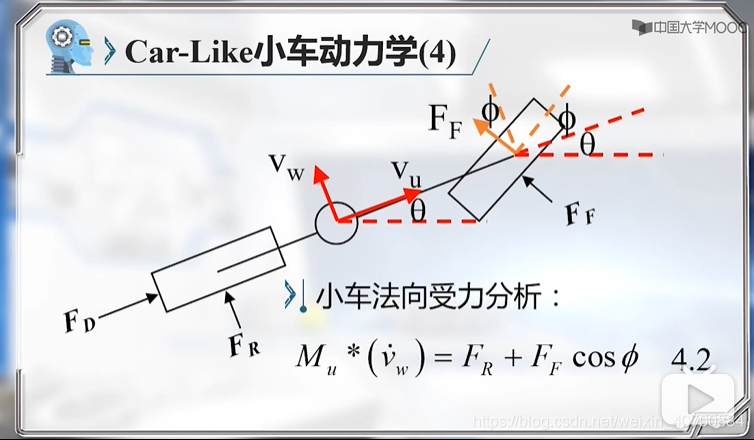
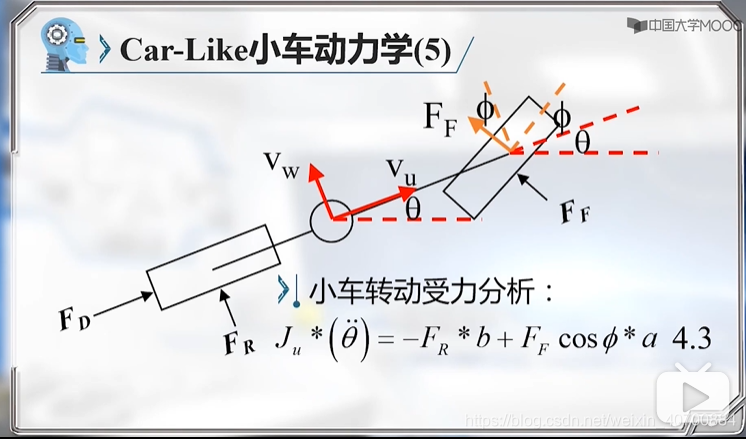

FR和FF是不知道的,所以是非完整约束问题。





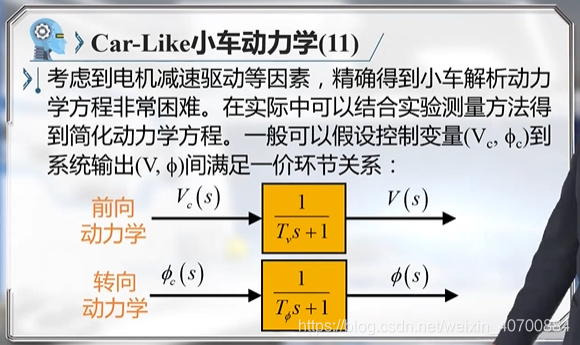
Tv和Tfai可以通过实验测量。
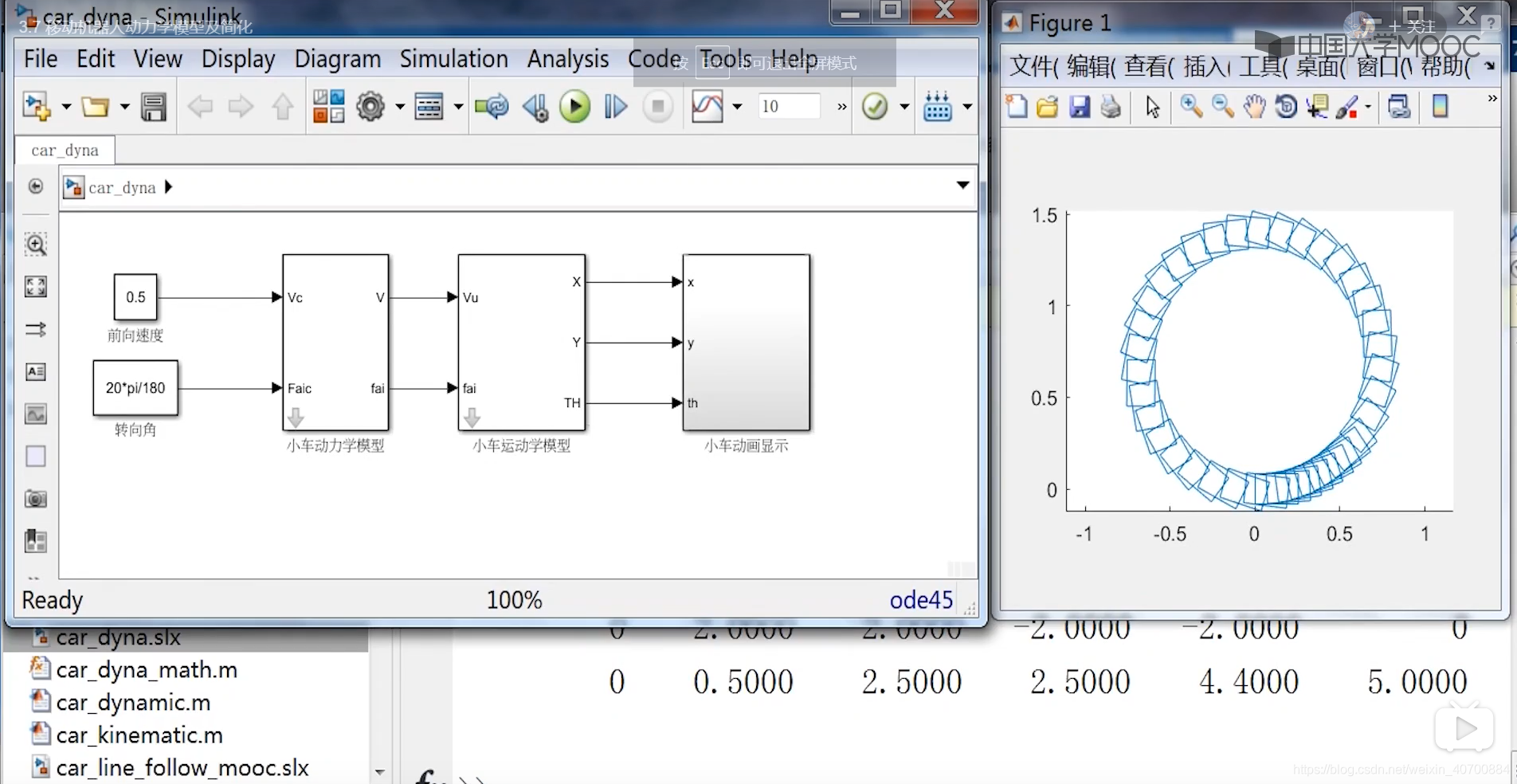
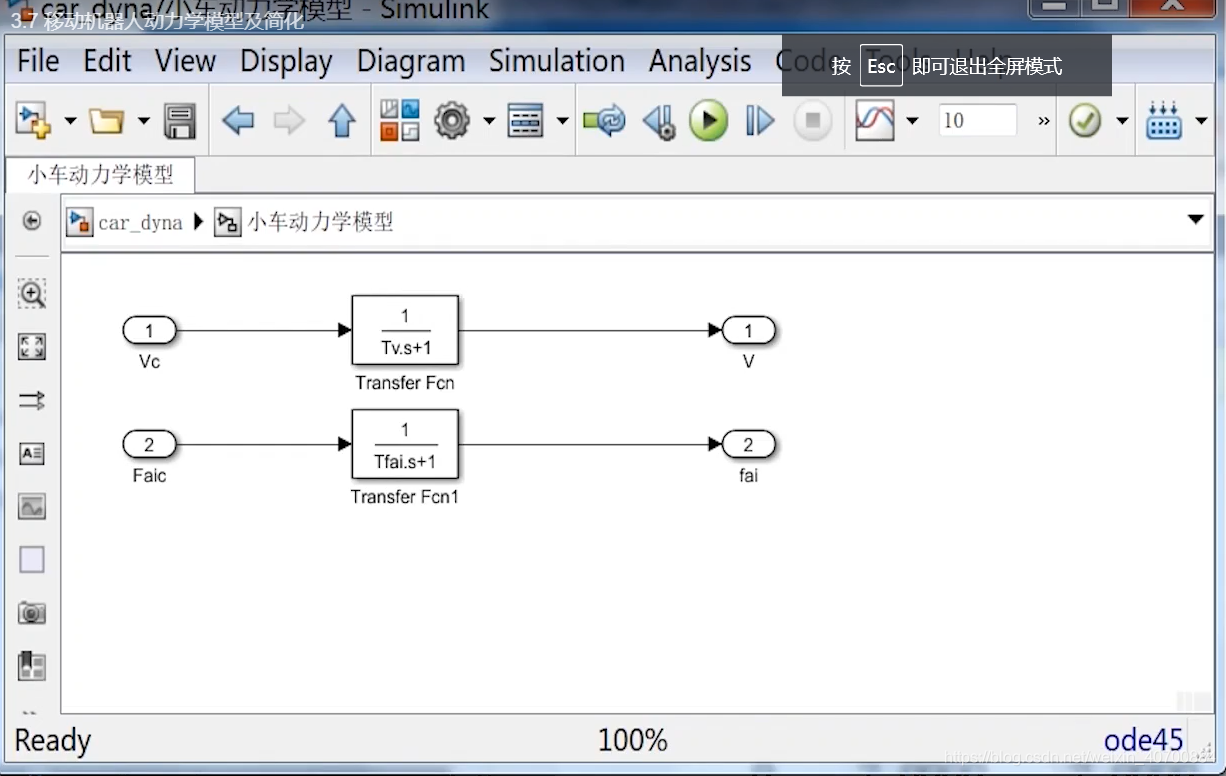
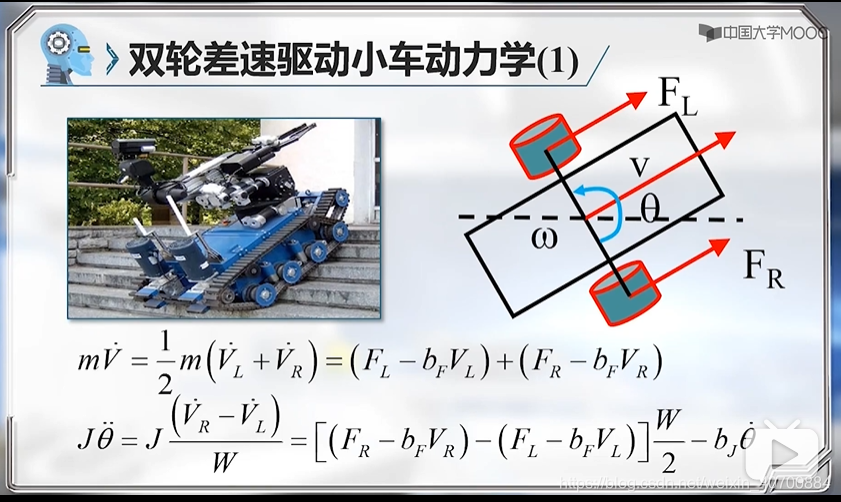

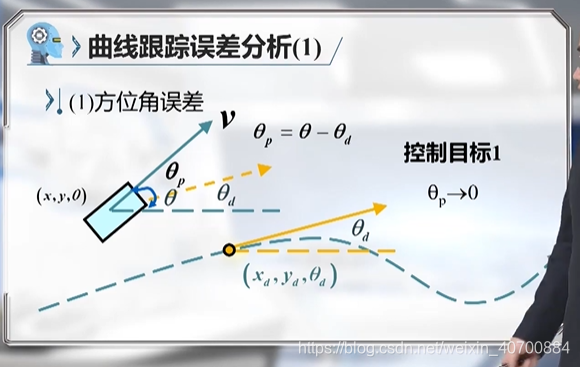
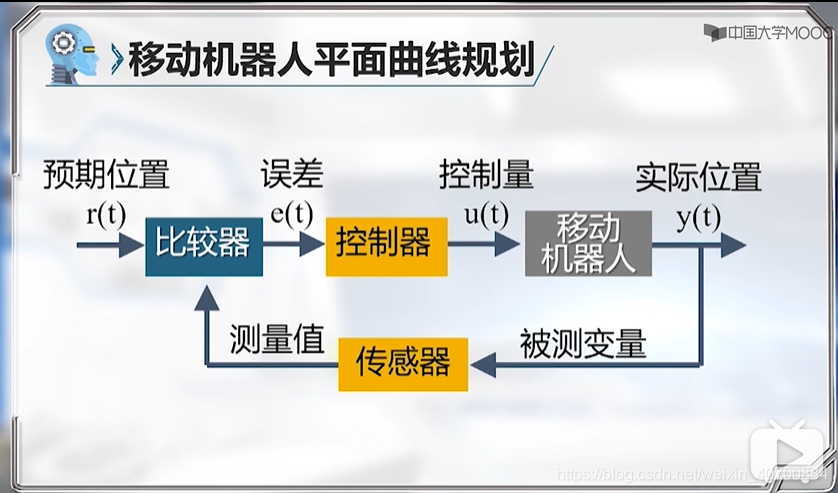
3.8 机器人路径跟踪控制—控制误差分析
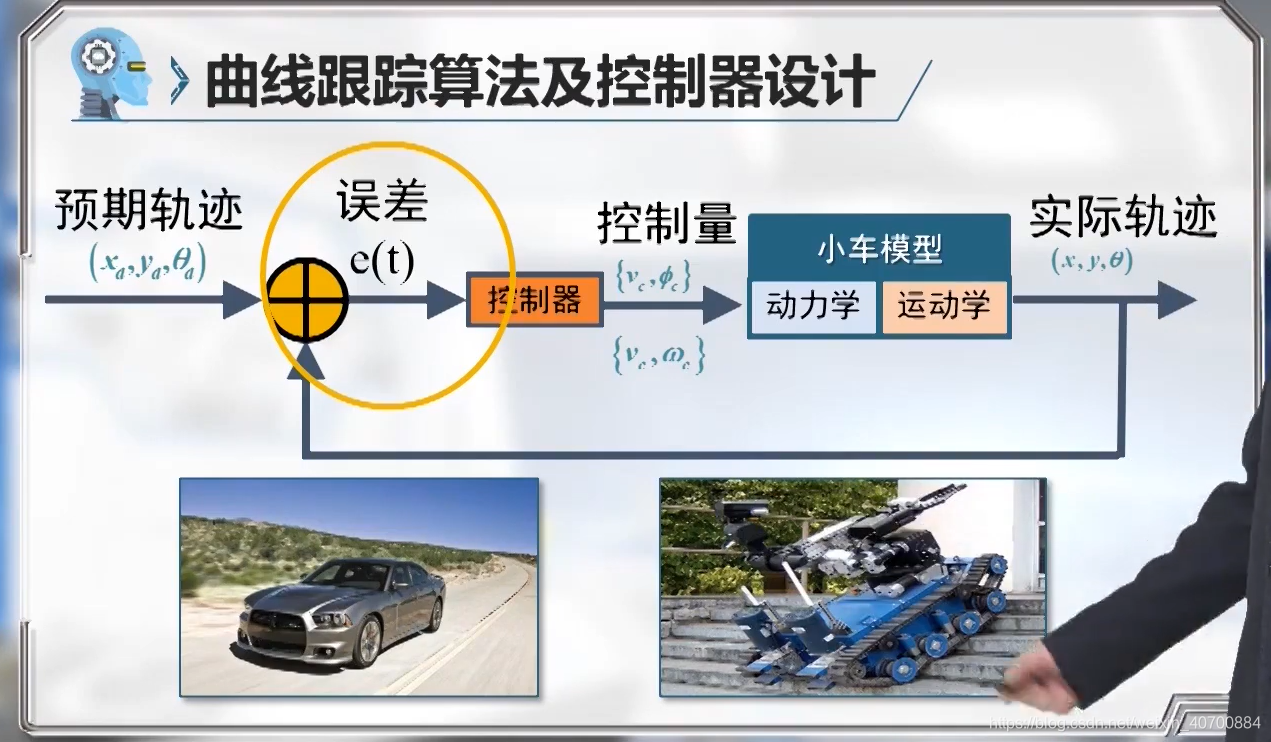
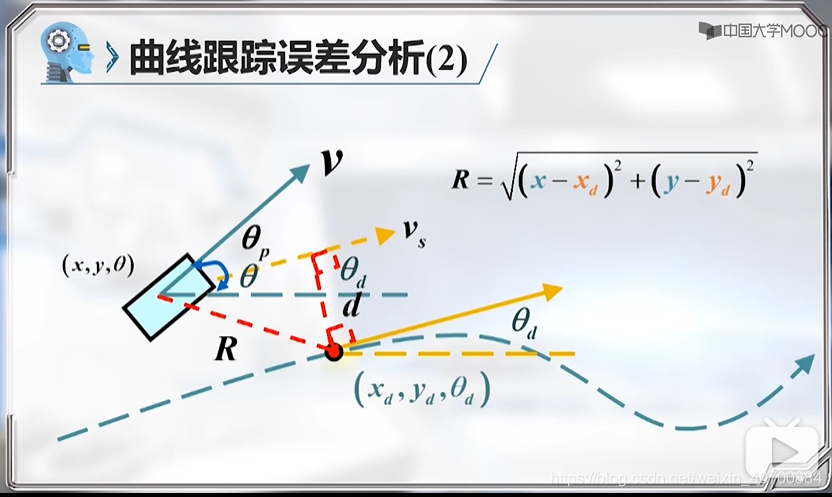
R是一个二维变量,可以在小车前向和法向上进行投影。
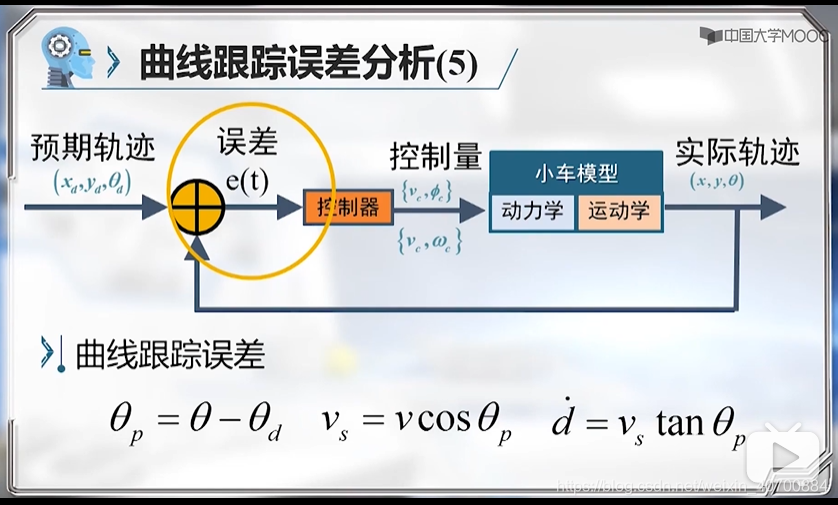
3.9 机器人路径跟踪控制—Car-Like小车曲线跟踪线性化模型及控制器设计


上边的方程都是非线性方程,需要线性化。
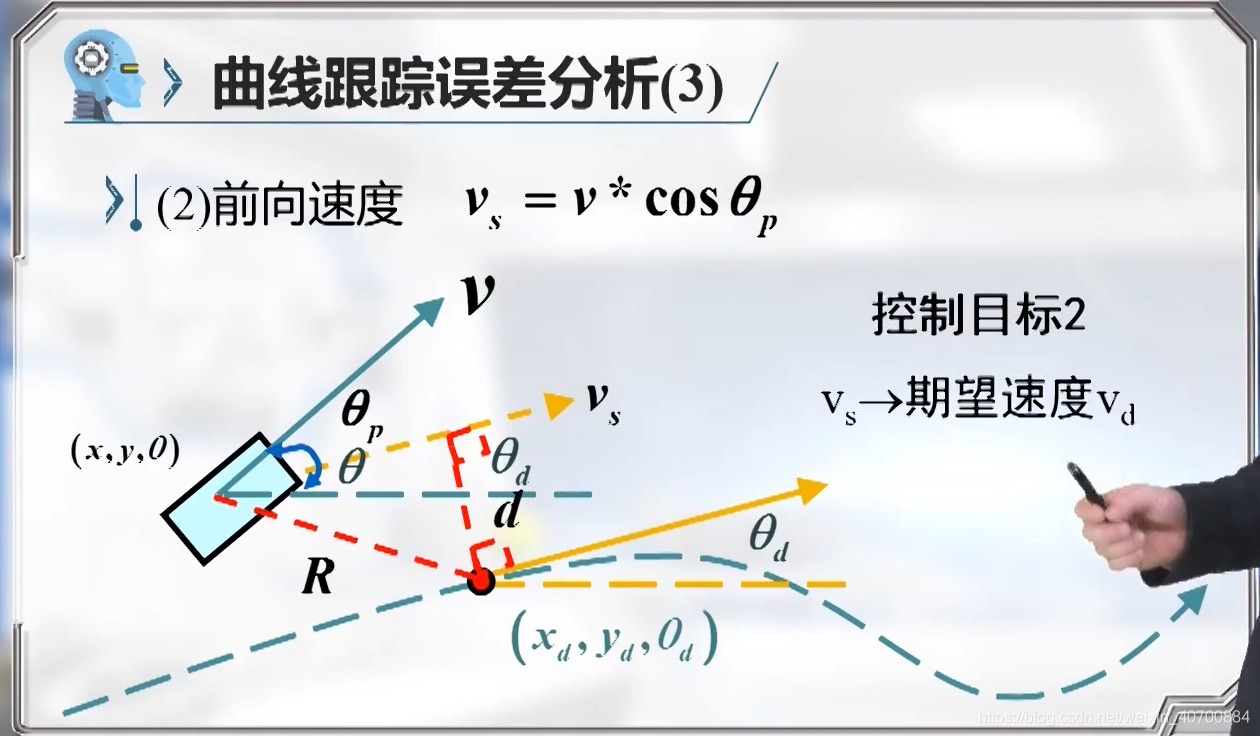
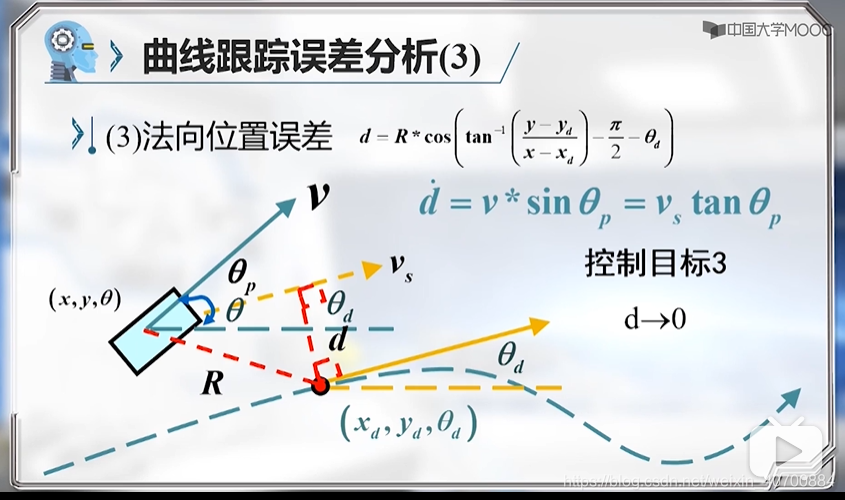
Vs代表小车沿着期望方向的前向速度,d为横向控制偏差,θp方位角偏差,fai为转向角。用这四个变量把这些方程描述清楚。
关于这四个变量的非线性方程,在工作点附近对其线性化。

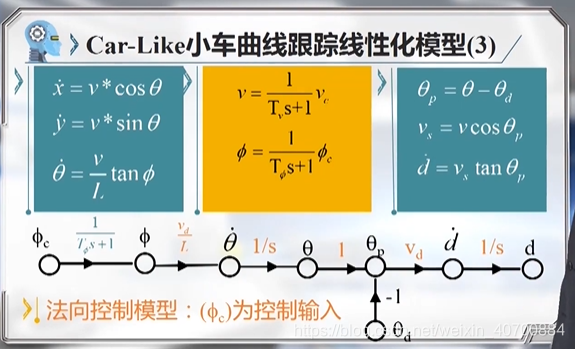
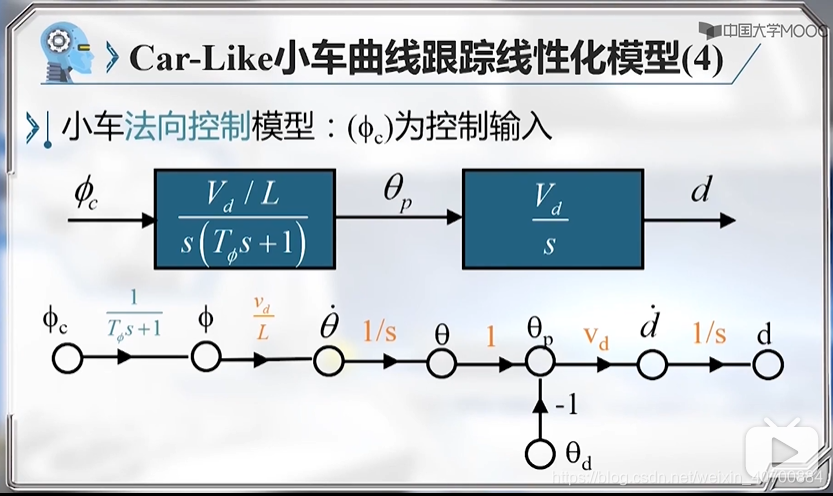
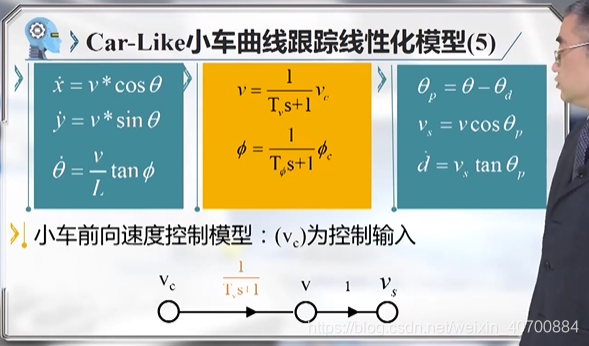
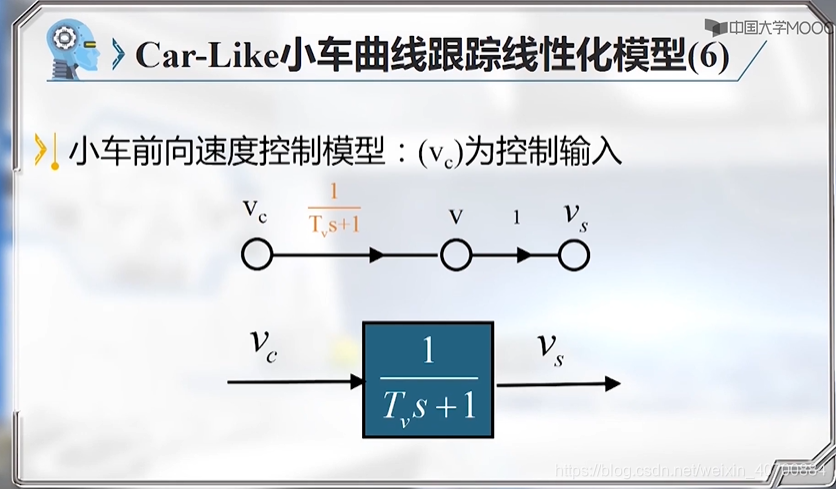
最终得到两个模型:横向偏差控制模型,三阶的模型;前向速度控制模型。
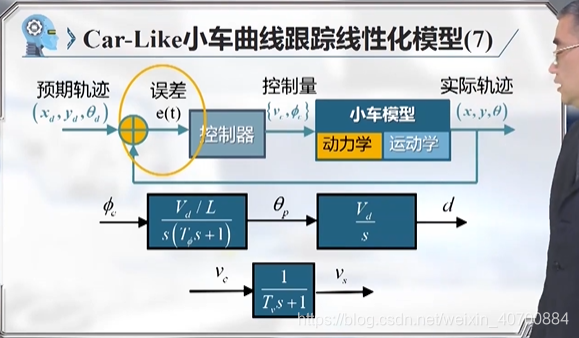
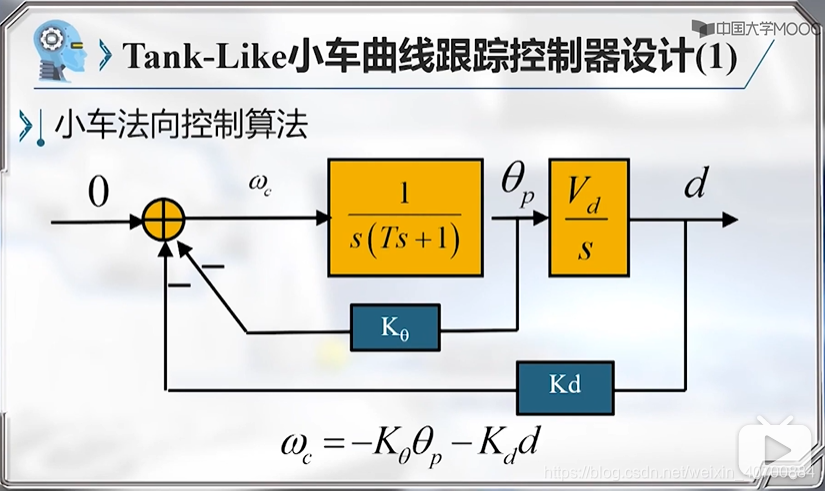
算法很多,下边是一个pd控制器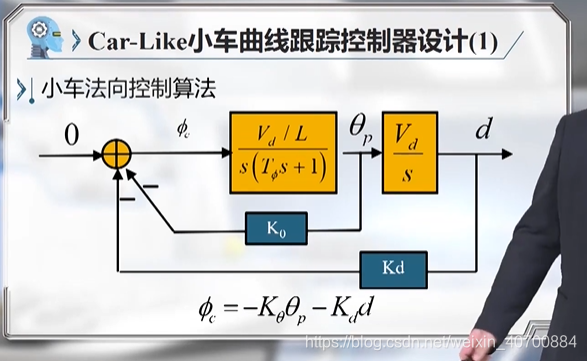
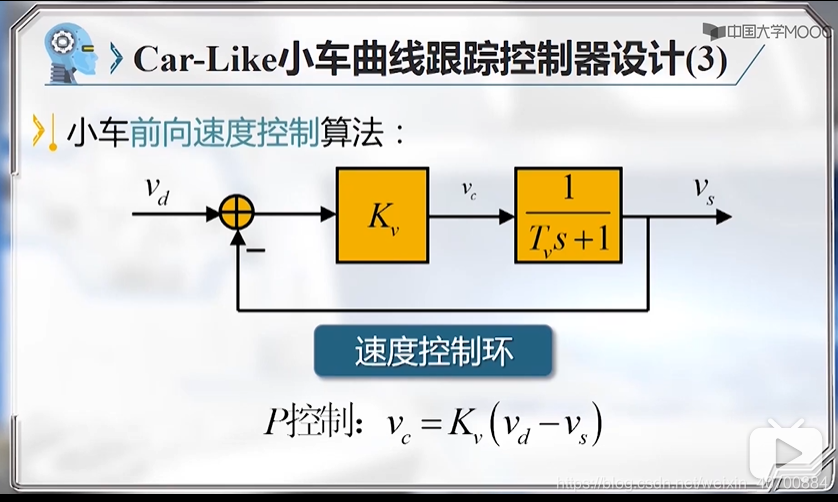
由此到得到小车曲线跟踪的两个法向和前向的线性模型。
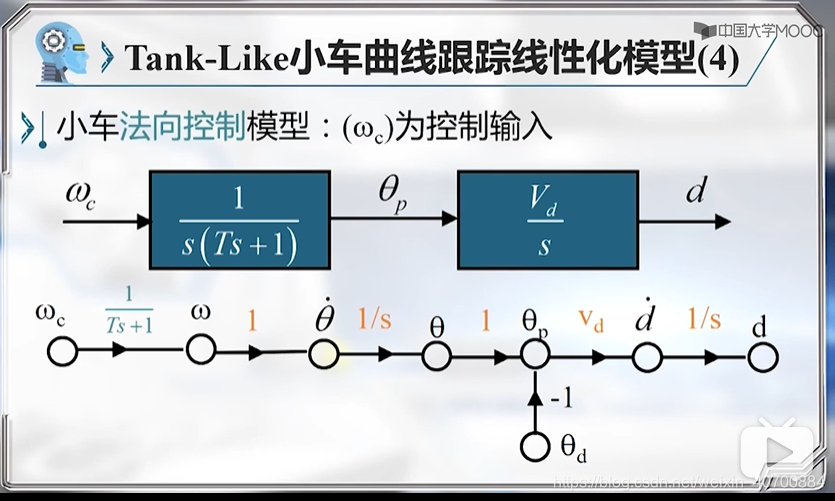
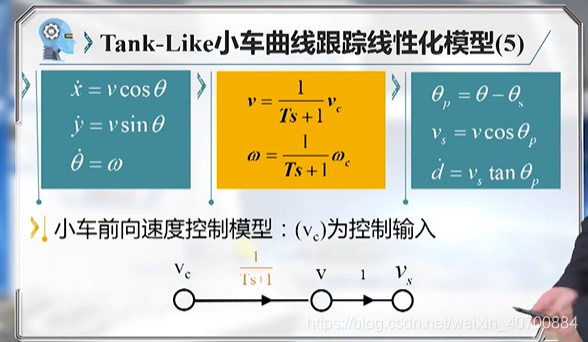
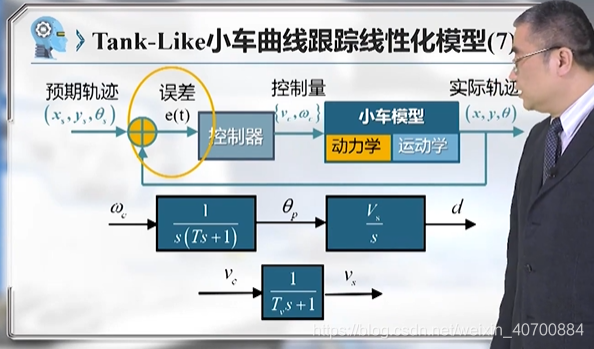
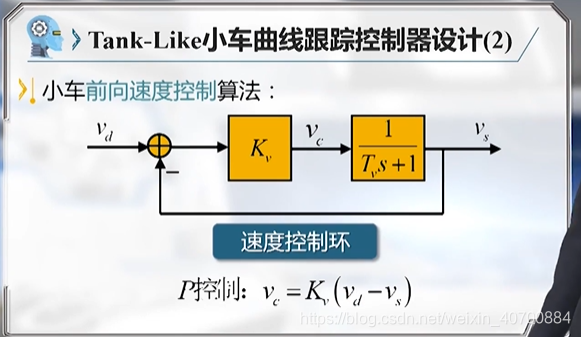
3.10 机器人路径跟踪控制—Tank-Like小车曲线跟踪线性化模型及控制器设计

用三元组描述,进行线性化
vs代表前向速度,d代表横向偏差,θp代表方位角误差。

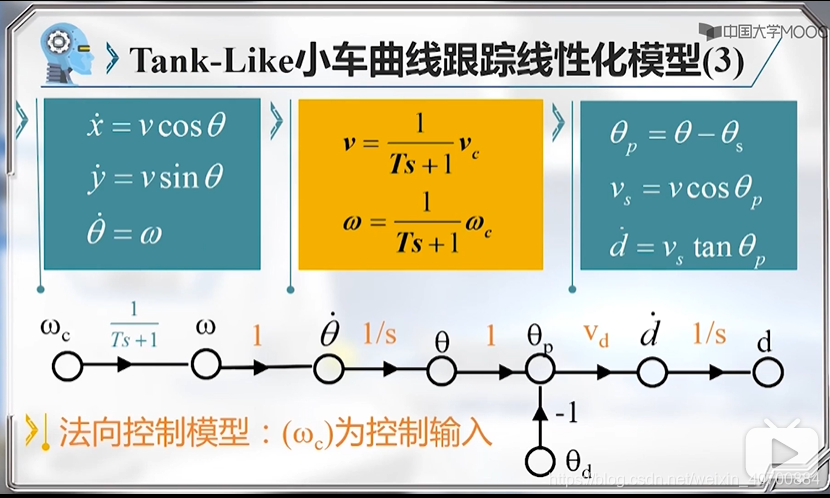
3.11 机器人运动控制总结

这篇关于智能机器人系统(国防科技大学)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







