HDU 2446 Shell Pyramid（二分查找 数学）

In the 17th century, with thunderous noise, dense smoke and blazing fire, battles on the sea were just the same as those in the modern times. But at that time, the cannon ,were extremely simple. It was just like an iron cylinder, with its rearward end sealed and forward end open. There was a small hole at the rearward end of it, which was used to install the fuse. The cannons on the warships were put on small vehicles which had four wheels and the shells were iron spheres with gunpowder in them.

At that time, it was said that there was an intelligent captain, who was also a mathematician amateur. He liked to connect everything him met to mathematics. Before every battle, he often ordered the soldiers to put the shells on the deck and make those shells to form shell pyramids.

Now let's suppose that a shell pyramid has four layers, and there will be a sequence of ordinal numbers in every layer. They are as the following figure:



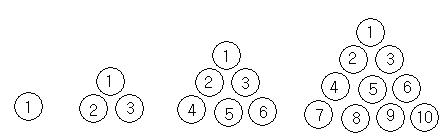
In the figure, they are the first layer, the second layer, the third layer and the fourth layer respectively from the left to the right.

In the first layer, there is just 1 shell, and its ordinal number is 1. In the second layer, there are 3 shells, and their ordinal numbers are 1, 2, and 3. In the third layer, there are 6 shells, and their ordinal numbers are 1, 2, 3, 4, 5, and 6. In the fourth layer, there are 10 shells, and their ordinal numbers are shown in the figure above.

There are also serial numbers for the whole shell pyramid. For example, the serial number for the third shell in the second layer is 4, the serial number for the fifth shell in the third layer is 9, and the serial number for the ninth shell in the fourth layer is 19.

There is also a interrelated problem: If given one serial number s, then we can work out the s th shell is in what layer, what row and what column. Assume that the layer number is i, the row number is j and the column number is k, therefore, if s=19, then i=4, j=4 and k=3.

Now let us continue to tell about the story about the captain.
A battle was going to begin. The captain allotted the same amount of shells to every cannon. The shells were piled on the deck which formed the same shell pyramids by the cannon. While the enemy warships were near, the captain ordered to fire simultaneously. Thunderous sound then was heard. The captain listened carefully, then he knew that how many shells were used and how many were left. 

At the end of the battle, the captain won. During the break, he asked his subordinate a question: For a shell pyramid, if given the serial number s, how do you calculate the layer number i, the row number j and column number k? 

First input a number n,repersent n cases.For each case there a shell pyramid which is big enough, a integer is given, and this integer is the serial number s（s<2^63）. There are several test cases. Input is terminated by the end of file.

For each case, output the corresponding layer number i, row number j and column number k.

  
2
19
75822050528572544

  
4 4 3
769099 111570 11179

2008 Asia Regional Harbin

#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
typedef __int64 LL;#define N 2000017
LL p[N] = {0}, sn[N] = {0};
//a每一个位置的数,b：SnLL findd1(LL n)
{LL s = 1, e = N, mid;while(s < e){mid = (s+e)/2;if(sn[mid] < n)s = mid+1;else if(sn[mid] > n)e = mid-1;elsereturn mid;}return s;
}LL findd2(LL n, LL endd)
{LL s = 1, e = endd, mid;while(s < e){mid = (s+e)/2;if(p[mid] < n)s = mid+1;else if(p[mid] > n)e = mid-1;elsereturn mid;}return s;
}int main()
{LL t;LL n;memset(p,0,sizeof(p));memset(sn,0,sizeof(sn));for(int i = 1; i < N; i++)//每一堆{p[i] = p[i-1]+i;}for(int i = 1; i < N; i++)//Sn{sn[i] = p[i]+sn[i-1];}/* for(int i = N-10; i < N; i++){printf("%I64d\n",sn[i]);}*///2^63 = 9223372036854775808scanf("%I64d",&t);while(t--){scanf("%I64d",&n);LL weizhi = findd1(n);// printf("pos:%I64d\n",weizhi);if(sn[weizhi] < n)weizhi+=1;LL tt = n-sn[weizhi-1];//本堆的个数LL r = findd2(tt,weizhi);//printf("R:%I64d\n",r);if(p[r] == tt){printf("%I64d %I64d %I64d\n",weizhi,r,r);}else{if(p[r] < tt)r++;LL c = tt - p[r-1];printf("%I64d %I64d %I64d\n",weizhi,r,c);}/*else{LL c = tt - p[r-1];printf("%I64d %I64d %I64d\n",weizhi,r,c);}*/}return 0;
}/*
2
14
15
*/