LeetCode 6076. 表示一个折线图的最少线段数

一、题目

1、题目描述

  给你一个二维整数数组 stockPrices，其中 stockPrices[i] = [dayi, pricei]表示股票在 dayi的价格为 pricei。折线图 是一个二维平面上的若干个点组成的图，横坐标表示日期，纵坐标表示价格，折线图由相邻的点连接而成。比方说下图是一个例子：

  样例输入： stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
  样例输出： 3

2、基础框架

• C++ 版本给出的基础框架代码如下：

class Solution {
public:int minimumLines(vector<vector<int>>& stockPrices) {}
};

3、原题链接

LeetCode 6076. 表示一个折线图的最少线段数

二、解题报告

1、思路分析

  $(1)$ 看到这道题，首先要想到给出的数据是不是按照 day单调递增的，如果不是则需要排序；
  $(2)$ 只有一个点的情况需要特殊处理；
  $(3)$ 如果一旦出现两个点或者以上，则线段至少需要一条，令计数器为1；
  $(4)$ 从第三个点开始枚举，看是否和前一个点共线，如果不共线，则需要多一条线段出来；
  $(5)$ 共线的判定，可以采用斜率相等，对于三个坐标 $(x_0,y_0),(x_1,y_1),(x_2,y_2)$，必须满足：
$$\frac{y_1-y_0}{x_1-x_0}=\frac{y_2-y_1}{x_2-x_1}$$
  $(6)$ 由于除法会带来精度问题，所以可以将这些坐标点都定义成 long long，然后判断如下等式是否成立：
$$(y_1-y_0)(x_2-x_1)==(y_2-y_1)(x_1-x_0)$$
  $(7)$ 不成立，则计数器加一；
  $(8)$ 最后返回计数器。

2、时间复杂度

   最坏时间复杂度 $O(nlo{g}_{2}n)$ 。

3、代码详解

class Solution {
public:int minimumLines(vector<vector<int>>& stockPrices) {int n = stockPrices.size();int i;if(n == 1) {return 0;}sort( stockPrices.begin(), stockPrices.end(), [&](const vector<int>& a, const vector<int>& b) {return a[0] < b[0];});int ans = 1;for(i = 2; i < n; ++i) {long long x0 = stockPrices[i-2][0], y0 = stockPrices[i-2][1];long long x1 = stockPrices[i-1][0], y1 = stockPrices[i-1][1];long long x2 = stockPrices[i-0][0], y2 = stockPrices[i-0][1];//  y1 - y0       y2 - y1//  x1 - x0   ==  x2 - x1if( (y1-y0)*(x2-x1) != (y2-y1)*(x1-x0) ) ++ans;}return ans;}
};

三、本题小知识

  精度问题一定要小心，能乘法的一定不要用除法。

四、加群须知

  相信看我文章的大多数都是「 大学生 」，能上大学的都是「 精英 」，那么我们自然要「 精益求精 」，如果你还是「 大一 」，那么太好了，你拥有大把时间，当然你可以选择「 刷剧 」，然而，「 学好算法 」，三年后的你自然「 不能同日而语 」。
  那么这里，我整理了「 几十个基础算法 」 的分类，点击开启：

  大致题集一览：

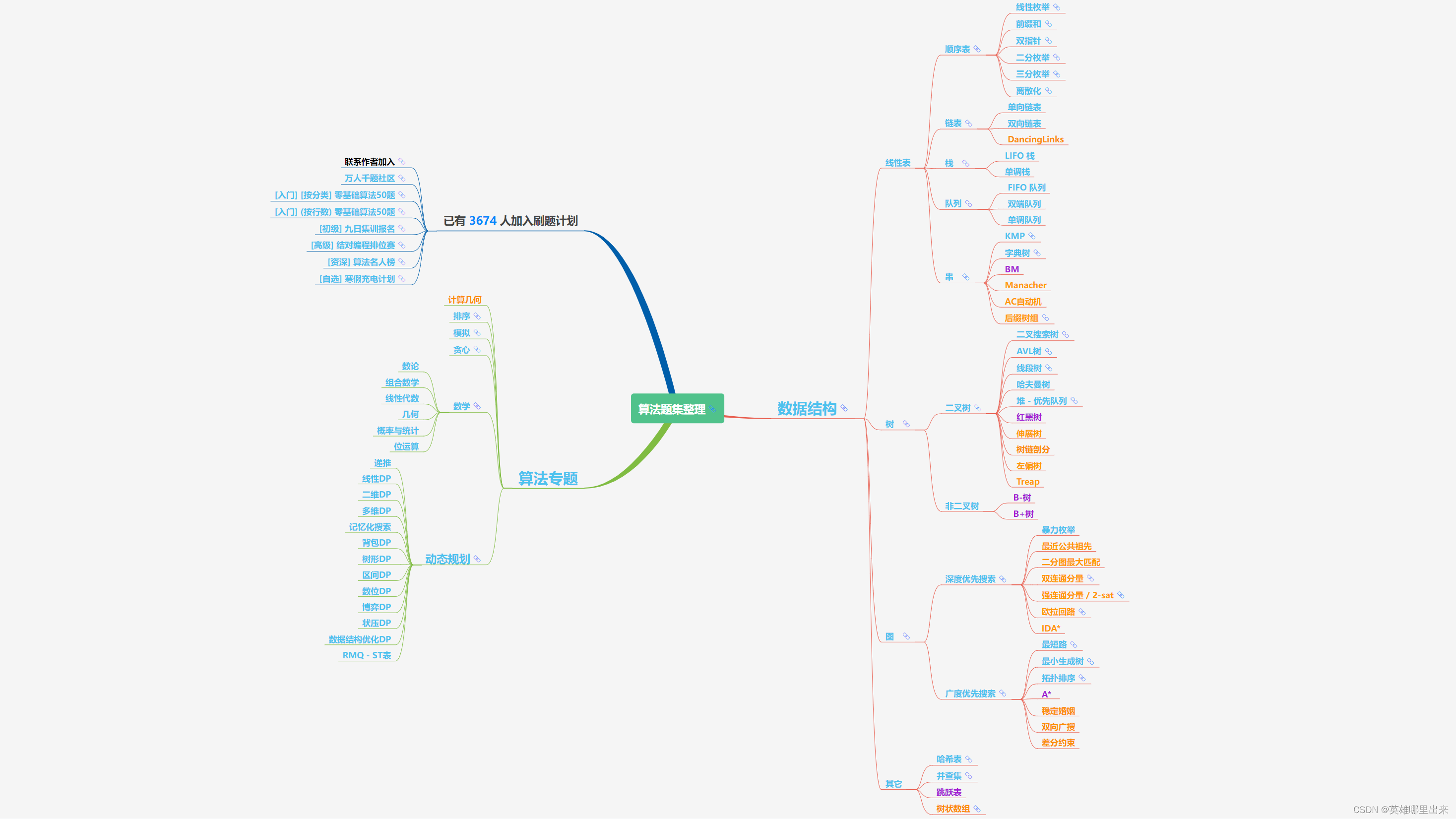
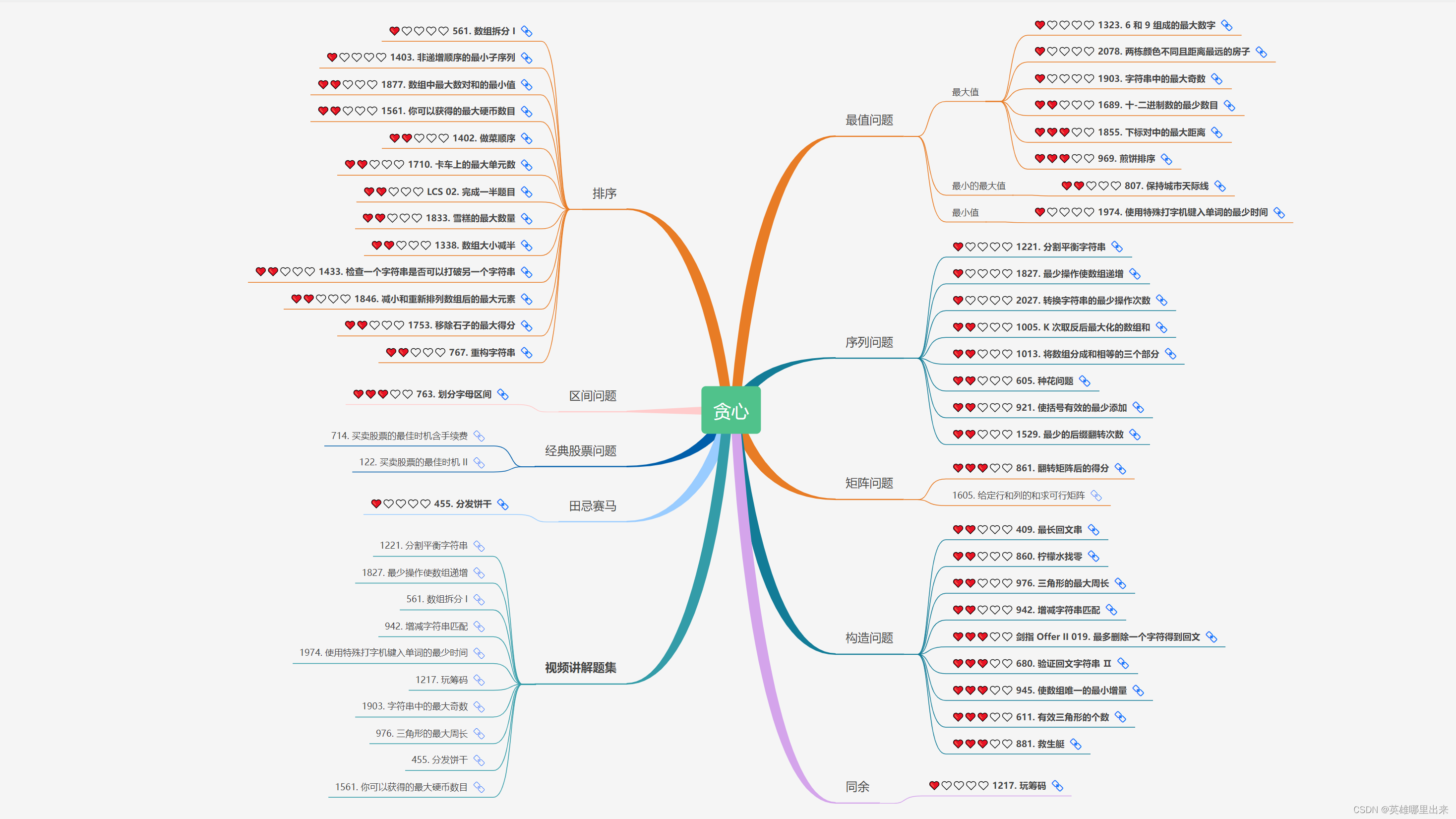
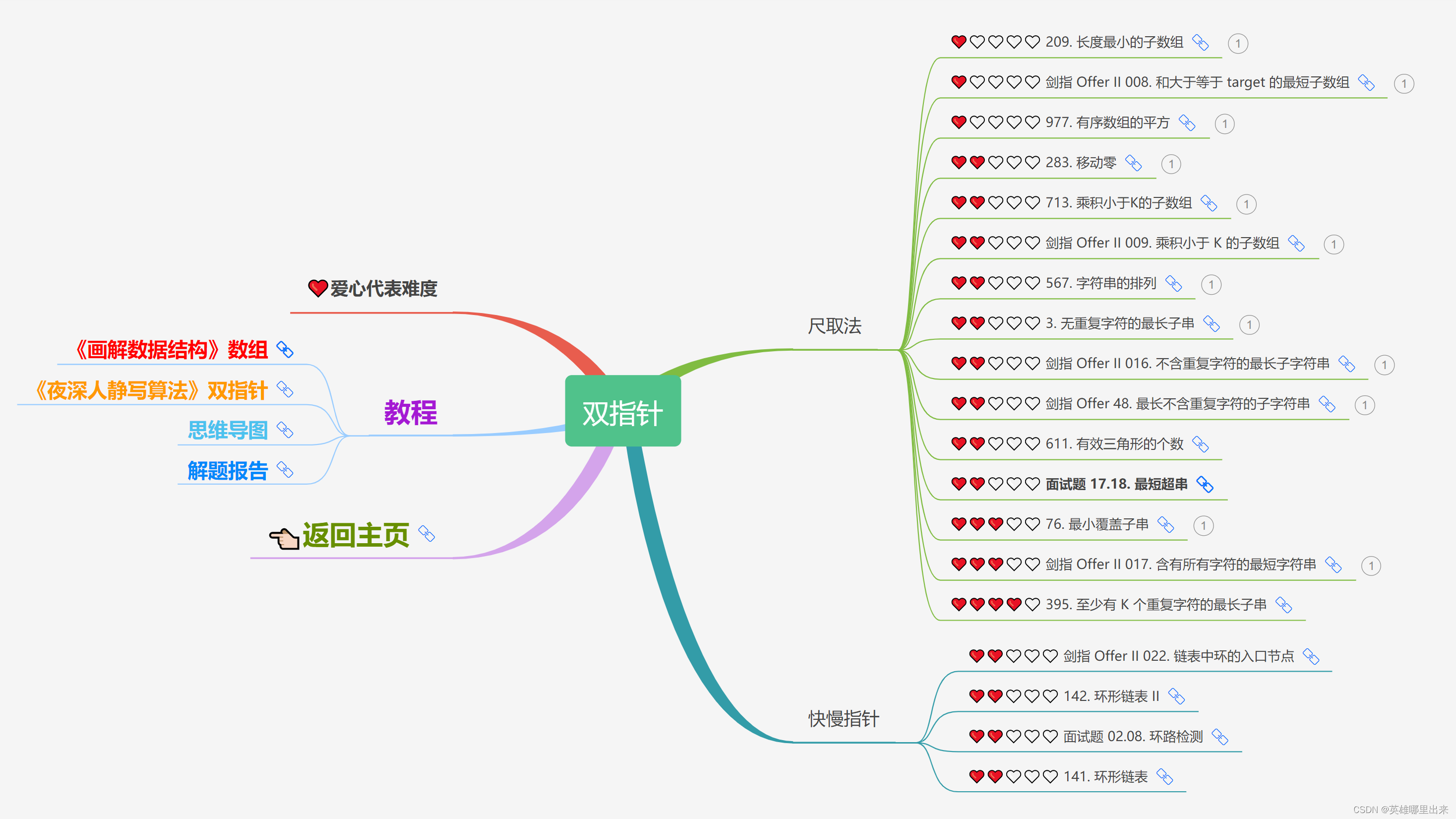
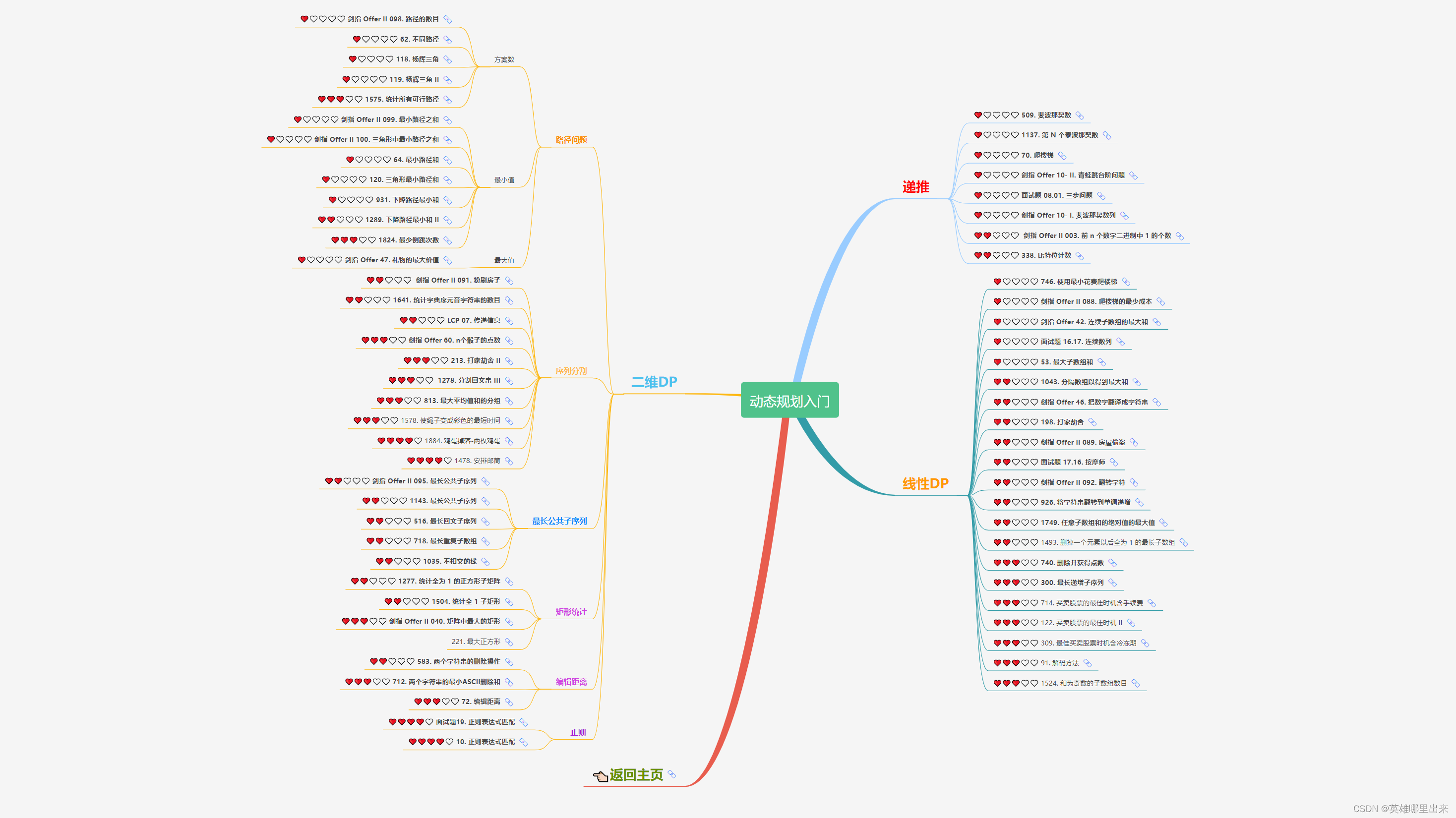
  为了让这件事情变得有趣，以及「 照顾初学者 」，目前题目只开放最简单的算法 「 枚举系列 」 （包括：线性枚举、双指针、前缀和、二分枚举、三分枚举），当有 一半成员刷完 「 枚举系列 」 的所有题以后，会开放下个章节，等这套题全部刷完，你还在群里，那么你就会成为「 夜深人静写算法 」专家团 的一员。
  不要小看这个专家团，三年之后，你将会是别人 望尘莫及 的存在。如果要加入，可以联系我，考虑到大家都是学生， 没有「 主要经济来源 」，在你成为神的路上，「 不会索取任何 」。
  🔥联系作者，或者扫作者主页二维码加群，加入刷题行列吧🔥

🔥让天下没有难学的算法🔥
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
让你养成九天持续刷题的习惯 🔥《九日集训》🔥
入门级C语言真题汇总 🧡《C语言入门100例》🧡
组团学习，抱团生长 🌌《算法零基础100讲》🌌
几张动图学会一种数据结构 🌳《画解数据结构》🌳
竞赛选手金典图文教程 💜《夜深人静写算法》💜