第七届集美大学程序设计竞赛（个人赛）题解

参考难度：
签到题：B、D
⭐：C
⭐⭐：H、J
⭐⭐⭐：I、G
⭐⭐⭐⭐：A、E、F

A. 送分题

思路

要算的式子可以变成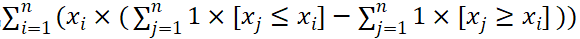
很明显按$x_i$大小顺序排序会很方便。因为要范围查询还有单点修改，所以用线段树或者平衡树。
假如用线段树的话，树的每个点代表区间$[l,r]$范围的答案，记录三个值，(数量，总和，答案)
叶子时，$l=r$，所以该点的值为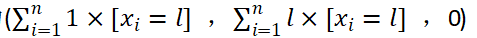

结合两个区间时 ，右区间的$l\ge$左区间的r，生成的点的值为(左区间数量+右区间数量，左区间总和+右区间总和 ，左区间答案+右区间答案+右区间总和左区间大小-左区间总和右区间大小) ，因为右区间内的任何一个$x_j$都比左区间内的$x_i$任何一个大 , 所以要$-$右区间数量$\ast$左区间总和，而左区间内部的$x_i$和$x_j$产生的答案已经在左区间答案记录了，不需要再算；右区间同理，只是要$+$。
平衡树时，因为每个点都代表一个$x_i$ ，所以根也要算上，每个子树当作一个区间。
方法有点像在排序后的数组上点分治。如果只看一个$x_i$,它跟排序后左边的区间结合，会$-$左区间数量$\ast x_i$,跟右边的区间结合，会右区间数量* ,直到扩展到要求的区间。
原题链接：https://codeforces.com/contest/295/problem/E

代码

参考答案：
动态线段树(作者：Arpa ,出题人微改)：

//God & me
#include <bits/stdc++.h>
#define pb push_back
#define X first
#define Y second
using namespace std;
template<class T,class L>bool smax(T&x,L y){return x<y?(x=y,1):0;}template<class T,class L>bool smin(T&x,L y){return x>y?(x=y,1):0;}
typedef pair<int,int> pii;const int maxn=1e5+17;
struct node{long long sum,ans;int cnt,s,e;node * l,* r;node (int c=0,long long ss=0,long long a=0,int st=-1e9,int en=1e9+1){cnt=c,sum=ss,ans=a,s=st,e=en,l=r=NULL;}node mrg(const node &od){return node(od.cnt+cnt, od.sum+sum , od.ans + ans + od.sum * cnt - sum * od.cnt);}void plant(){int mid=(s+e)/2;if(l==NULL)l=new node(0,0,0,s,mid);if(r==NULL)r=new node(0,0,0,mid,e);}node smoke(int st,int en){if(st<=s && e<=en)return *this;if(en<=s || e<=st)return node();plant();return (l -> smoke(st,en)).mrg(r -> smoke(st,en));}void water(int p,int nut=1){if(s+1==e){cnt+=nut, ans=0,sum=cnt*p;return ;}int mid=(s+e)/2;plant();if(p<mid)l -> water(p,nut);elser -> water(p,nut);node tmp=l -> mrg(*r);cnt=tmp.cnt , ans = tmp.ans , sum = tmp.sum;}
}*root;
int n,p[maxn];
int main(){ios::sync_with_stdio(0),cin.tie(0);root = new node();cin>>n;for(int i=0;i<n;i++)cin>>p[i],root->water(p[i]);int q;cin>>q;for(int t,x,y;q--;){cin>>t>>x>>y;if(t==1)root->water(p[--x],-1),root->water(p[x]+=y);elsecout<<root->smoke(x,y+1).ans<<endl;}return 0;
}

离散化线段树(作者：Keshi)：
//In the name of GOD
#include <bits/stdc++.h>
using namespace std;typedef long long ll;const ll maxn = 2e6 + 100;
const ll mod = 1e9 + 7;
const ll inf = 1e18;#define fast_io ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define file_io freopen("input.txt" , "r+" , stdin) ; freopen("output.txt" , "w+" , stdout);
#define pb push_back
#define Mp make_pair
#define pll pair<ll, ll>
#define F first
#define S secondstruct dat{ll cnt, sum, dis;
};ll n, m, k, a[maxn], b[maxn];
dat seg[maxn];
vector<ll> p;
vector<pair<ll, pll> > q;
vector<dat> vec;dat mrg(dat p1, dat p2){dat p3;p3.cnt = p1.cnt + p2.cnt;p3.sum = p1.sum + p2.sum;p3.dis = p1.dis + p2.dis + p1.cnt * p2.sum - p1.sum * p2.cnt;return p3;
}void upd(ll id, ll s, ll e, ll l, ll x, ll y){if(l < s || e <= l) return;if(e - s == 1){seg[id].cnt += x;seg[id].sum += y;return;}ll mid = (s + e) / 2;upd(id * 2, s, mid, l, x, y);upd(id * 2 + 1, mid, e, l, x, y);seg[id] = mrg(seg[id * 2], seg[id * 2 + 1]);return;
}
void get(ll id, ll s, ll e, ll l, ll r){if(r <= s || e <= l) return;if(l <= s && e <= r){vec.pb(seg[id]);return;}ll mid = (s + e) / 2;get(id * 2, s, mid, l, r);get(id * 2 + 1, mid, e, l, r);return;
}
ll solve(ll l, ll r){vec.clear();get(1, 0, k, l, r);for(ll i = 1; i < vec.size(); i++){vec[i] = mrg(vec[i - 1], vec[i]);}if(vec.empty()) return 0;return vec[vec.size() - 1].dis;
}int main(){fast_io;ll t, l, r;cin >> n;for(ll i = 0; i < n; i++){cin >> a[i];b[i] = a[i];p.pb(b[i]);}cin >> m;for(ll i = 0; i < m; i++){cin >> t >> l >> r;q.pb(Mp(t, Mp(l, r)));if(t == 1){b[l - 1] += r;p.pb(b[l - 1]);}}sort(p.begin(), p.end());k = p.size();for(ll i = 0; i < n; i++){upd(1, 0, k, lower_bound(p.begin(), p.end(), a[i]) - p.begin(), 1, a[i]);}for(ll i = 0; i < m; i++){t = q[i].F;l = q[i].S.F;r = q[i].S.S;if(t == 1){upd(1, 0, k, lower_bound(p.begin(), p.end(), a[l - 1]) - p.begin(), -1, -a[l - 1]);a[l - 1] += r;upd(1, 0, k, lower_bound(p.begin(), p.end(), a[l - 1]) - p.begin(), 1, a[l - 1]);}else{cout << solve(lower_bound(p.begin(), p.end(), l) - p.begin(), upper_bound(p.begin(), p.end(), r) - p.begin()) << '\n';}}return 0;
}

平衡树treap:

#include<bits/stdc++.h>
using namespace std;mt19937 rnd(time(0));struct item{int key,prior;int sz;long long sum;long long ans;int l,r;item(){}item(int key):key(key),prior(rnd()),sz(1),ans(0),sum(key),l(0),r(0){}
}tree[200010];int tcnt=0;int new_item(int key){tree[++tcnt]=item(key);return tcnt;
}int cnt(int it){return it?tree[it].sz:0;
}long long sum(int it){return it?tree[it].sum:0LL;
}long long ans(int it){return it?tree[it].ans:0LL;
}void upd(int it){if(it){int l=tree[it].l,r=tree[it].r;tree[it].sz=1+cnt(l)+cnt(r);tree[it].sum=tree[it].key+sum(l)+sum(r);tree[it].ans=1LL*(cnt(l)-cnt(r))*tree[it].key+1LL*(cnt(l)+1)*sum(r)-1LL*(cnt(r)+1)*sum(l)+ans(l)+ans(r);}
}void split(int t,int key,int &l,int &r){if(!t){l=r=0;return;}if(tree[t].key<=key)split(tree[t].r,key,tree[t].r,r),l=t;else split(tree[t].l,key,l,tree[t].l),r=t;upd(t);
}void merge(int &t,int l,int r){if(!l||!r)t=l?l:r;else if(tree[l].prior>tree[r].prior)merge(tree[l].r,tree[l].r,r),t=l;else merge(tree[r].l,l,tree[r].l),t=r;upd(t);
}void join(int &t,int p,int q){if(!p||!q){t=p?p:q;return ;}if(tree[p].prior<tree[q].prior)swap(p,q);int l,r;split(q,tree[p].key-rnd()%2,l,r);join(tree[p].l,tree[p].l,l);join(tree[p].r,tree[p].r,r);t=p;upd(t);
}void erase(int &t,int key){if(!t)return;if(tree[t].key==key){merge(t,tree[t].l,tree[t].r);}else erase(tree[t].key<key?tree[t].r:tree[t].l,key);upd(t);
}long long out(int &t,int l,int r){int lf,seg,rf;split(t,l-1,lf,seg);split(seg,r,seg,rf);long long ans=tree[seg].ans;merge(t,lf,seg);merge(t,t,rf);return ans;
}int main(){freopen("10//in.txt","r",stdin);freopen("10//out.txt","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,m;int root=0;cin>>n;vector<int > X(n);for(int i=0;i<n;i++){cin>>X[i];join(root,root,new_item(X[i]));}cin>>m;for(int i=0;i<m;i++){int op;cin>>op;if(op==1){int p,d;cin>>p>>d;p--;erase(root,X[p]);X[p]+=d;join(root,root,new_item(X[p]));}else {int l,r;cin>>l>>r;long long ans=out(root,l,r);cout<<ans<<endl;}}
}

---

---

B. 数列问题

题意

给定一个7个数的数列，其中两个数x1,x2是未知数，给出其中一个未知数x1的值，问另一个未知数x2可以取什么值使得数列可以构造出一个通项公式。

解题思路

任何有限数列都可以使用多项式拟合，所以不管给定的x1是什么，x2都可以是任何值。

换句话说，x1,x2是什么根本就不影响数列是否可以构造一个通项公式。

故输出一个合法的数字即可。（输出2个以上数字或者其他字符则不行）

代码

#include<stdio.h>
int main()
{printf("0");
}

---

---

C. 勋总的英语试卷

题意

有若干选择题，有单选或者多选，每次提交答案后，都能得到反馈，即每道题目是否正确，多选题当且仅当所有选项都选对时才会反馈正确，求至多多少次提交可以答对所有题。

思路

假如只有单选题，那提交次数最多为max(每到题目的选项数)，如果只有多选题的话，所有的组合情况为$2^n-1$次，因为至少要选一个选项。（n为max(每道题目的选项数))

代码

#include <bits/stdc++.h>
using namespace std;long long qpow(long long x, long long y) {long long ans = 1;while (y) {if (y & 1)ans = ans * x;y >>= 1;x = x * x;}return ans;
}int main() {ios::sync_with_stdio(false);int n;cin >> n;long long num;char ch;long long cnt1 = 0;long long cnt2 = 0;for (int i = 0; i < n; i++) {cin >> ch >> num;if (ch == 'S') {cnt1 = max(num, cnt1);} else {cnt2 = max(cnt2, num);}}long long ans1 = qpow(2, cnt2)-1;cout << max(ans1, cnt1) << endl;return 0;
}

---

---

D. 签到题

题意

输出一个小写字母满足：

• 这个字母是陕西省英文的第四个字母
• 这个字母的美国信息交换标准代码是97
• 这个字母是字符串"ax"和"xa"的LCS（最长公共子序列）

解题思路

• 陕西省英文：Shaanxi Province
• 'a’的美国信息交换标准代码（ASCII码）是97
• 字符串"ax"和"xa"的LCS是’a’或者’x’

代码

#include<stdio.h>
int main()
{printf("a");
}

---

---

E. csgo

解题思路

一个很简单的小常识：想求一个多边形的面积，先定一个原点，逆时针沿着多边形的边，每条边计算原点到边的两个端点的向量叉积/2，加起来，就是多边形面积。

图1（黑色线是多边形，红色点是我们定的原点）

图2(浅蓝色叉积大小为正，深蓝色叉积大小为负)

图3(浅蓝色叉积大小为正，深蓝色叉积大小为负)

图4(浅蓝色叉积大小为正，深蓝色叉积大小为负)

图5(浅蓝色叉积大小为正，深蓝色叉积大小为负)

图6(浅蓝色叉积大小为正，深蓝色叉积大小为负，先浅加了再深减了，所以那部分面积没有被累加)
因为任意三点不共线，我们可以把任意反恐精英的坐标变成原点，预处理每两个反恐精英的位置和原点组成三角形包含的恐怖分子的数量，记为$dp[i][j]$，像面积一样，只是把面积大小换成了包含的恐怖分子的数量，如果原点到两个反恐精英位置的向量叉积是正的就加包含恐怖分子的数量，如果原点到两个反恐精英位置的向量叉积是负的就减包含恐怖分子的数量。如果$\overrightarrow{Oi}$到$\overrightarrow{Oj}$是逆时针方向，则$\overrightarrow{Oj}$到$\overrightarrow{Oi}$是顺时针方向，所以$dp[i][j]=-dp[j][i]$。复杂度$O(N^{2}M)$
每次询问，就把反恐精英的点求一次凸包，然后逆时针沿着凸包的边，每个边有两个点，假如边的出发端点是$i$，边的终止端点是$j$，把预处理$dp[i][j]$加起来，就是询问的答案。复杂度$O(\sum klogk+k)$
原题链接：https://www.codechef.com/problems/CHEFPOLY

代码

#include<bits/stdc++.h>
using namespace std;using Point=complex<int >;int dot(Point a,Point b){return (conj(a)*b).real();
}int cross(Point a,Point b){return (conj(a)*b).imag();
}bool belong(Point A,Point B,Point C,Point P){return abs(cross(B-A,C-A))==abs(cross(A-P,B-P))+abs(cross(B-P,C-P))+abs(cross(C-P,A-P));
}int sign(int v){return v==0?0:v>0?1:-1;
}vector<int > getConvex_Hull(const vector<int >& V,const vector<Point >& R){int len=V.size();vector<int > newV(V.begin(),V.end());sort(newV.begin(),newV.end(),[&](int x,int y){return R[x].real()==R[y].real()?R[x].imag()<R[y].imag():R[x].real()<R[y].real();});Point rot[2]={{0,1},{0,-1}};vector<int > hull[2]={{newV[0]},{newV[0]}};for(int k=0;k<2;k++){vector<Point> vers;for(int i=1;i<len;i++){while(vers.size()&&dot(vers.back(),R[newV[i]]-R[hull[k].back()])<=0){hull[k].pop_back();vers.pop_back();}vers.push_back((R[newV[i]]-R[hull[k].back()])*rot[k]);hull[k].push_back(newV[i]);}}reverse(hull[1].begin(),hull[1].end());hull[0].insert(hull[0].end(),hull[1].begin()+1,hull[1].end()-1);return hull[0];
}int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int N,M;cin>>N>>M;vector<Point> R(N),B(M);for(auto &r:R){int x,y;cin>>x>>y;r={x,y};}for(auto &b:B){int x,y;cin>>x>>y;b={x,y};}Point O(R[0]);for(auto &r:R){r-=O;}for(auto &b:B){b-=O;}O={0,0};vector<vector<int > > T(N,vector<int >(N)); for(int i=0;i<N;i++){for(int j=i+1;j<N;j++){int signq=sign(cross(R[i],R[j]));if(signq==0)continue;for(int k=0;k<M;k++){if(belong(O,R[i],R[j],B[k])){T[i][j]+=signq;T[j][i]-=signq;}}}}int Q;cin>>Q;for(int i=0;i<Q;i++){//cerr<<i<<endl;int ans=0;int k;cin>>k;//cerr<<k<<endl;vector<int > V(k); for(auto &v:V){cin>>v;v--;}V=getConvex_Hull(V,R);k=V.size();for(int j=0;j<k;j++){//cerr<<V[j]<<' ';int net=(j+1)%k;ans+=T[V[j]][V[net]];}//cerr<<endl;cout<<abs(ans)<<endl;}

---

---

F. Total order

解题思路

样例很明显的暗示，如果是环答案就是$0$，如果不是环那就是树或森林。先按照输入建图，每个同学都连向他想超越的同学（无向图，有向图的话是他想超越的同学指向他自己），如果是自己，则连向一个虚假的最后同学（第$n+1$个同学）。假如判断没有环，则这是一棵树，根是那个虚假的同学。
现在我们想要的是一个排列，假如每个子树都代表它能构成排列的数量。
叶子的时候，答案是$1$，只有自己。
当点不是叶子的时候，它会有很多子树（也可能1个），这些子树都已经变成了排列，我们需要把这些排列随意相互合并即可，但原来子树的排列的前后顺序不能交换，然后把点作为最后的同学就形成新的排列。假设现在这个点有k个子树，每个子树大小为$le{n}_1,le{n}_2,le{n}_3,...,le{n}_k$，子树都已经变成了排列，则合并种类有$C_{le{n}_1+le{n}_2+le{n}_3+...+le{n}_k}^{le{n}_1}\ast C_{le{n}_2+le{n}_3+...+le{n}_k}^{le{n}_2}\ast ...\ast C_{le{n}_k}^{le{n}_k}$种，即$\frac{(le{n}_1+le{n}_2+le{n}_3+...+le{n}_k)!}{le{n}_1!le{n}_2!le{n}_3!...le{n}_k!}$。
(可以看作为从$(0,0,0,...0)$走到$(len1,len2,len3,...lenk)$,但每次只能移动$(1,0,0,...0)or(0,1,0,...0)or(0,0,1,...0)or...or(0,0,0,...1)$，的路径数。)。然后这个点和它的子树也是一个子树，这个子树的排列数量为：$\frac{(le{n}_1+le{n}_2+le{n}_3+...+le{n}_k)!}{le{n}_1!le{n}_2!le{n}_3!...le{n}_k!}$×点的子树1的排列数量×点的子树2的排列数量×点的子树3的排列数量×…×点的子树k的排列数量。
算到根的位置，就是符合要求的全部排列数量。
因为答案要模$1000000007$，所以用线性逆的话复杂度是$O(n)$,用快速幂求逆的话复杂度为$O(nlogn)$。

代码

#include<bits/stdc++.h>
using namespace std;const long long mod=1e9+7;long long fact[100010];long long fpow(long long a,long long b){long long z=1;while(b){if(b&1)z=z*a%mod;a=a*a%mod;b>>=1;}return z;
}long long inv(long long x){return fpow(x,mod-2);
}vector<int > G[100001];int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);fact[0]=1;for(int i=1;i<=100000;i++){fact[i]=fact[i-1]*i%mod;}int n;cin>>n;vector<int > a(n+1);for(int i=1;i<=n;i++){cin>>a[i];if(a[i]<1||a[i]>n)cerr<<"error"<<endl;}vector<int  > vis(n+1);bool loop=false;for(int i=1;i<=n;i++){if(!vis[i]){int cur=i;do{//cout<<cur<<endl;vis[cur]=i;cur=a[cur];if(cur!=a[cur]&&vis[cur]==i){loop=true;break;}}while(a[cur]!=cur&&vis[cur]==0);}}//cout<<"yes"<<endl;if(loop){//cout<<"loop"<<endl;cout<<0<<endl;return 0;}for(int i=1;i<=n;i++){if(a[i]!=i)G[a[i]].push_back(i);elseG[0].push_back(i);}vector<int > sz(n+1);function<void (int )> dfsz=[&](int u)->void{sz[u]=1;for(int v:G[u]){dfsz(v);sz[u]+=sz[v];}};dfsz(0);function<long long(int ,int )> C=[&](int p,int q)->long long{return fact[p]*inv(fact[q])%mod*inv(fact[p-q])%mod;};function<long long (int )> dfs=[&](int u)->long long{long long ans=1;int subsz=0;for(int v:G[u]){ans=(ans*dfs(v))%mod;subsz+=sz[v];//if(u==0){//cerr<<sz[v]<<endl;//}}for(int v:G[u]){ans=(ans*C(subsz,sz[v]))%mod;subsz-=sz[v];}return ans;};long long ans=dfs(0);cout<<ans<<endl;
}

原题网址：https://ac.nowcoder.com/acm/problem/229386
(原题n≤10,但出题人没想到是的复杂度$n!$,而且$10!$居然只有$3\ast 10^5$，所以想到了这个方法，因为考虑到大部分人都不会线性逆，便定$n\le 10^5$。)

---

---

G. 史上最强控分选手LJL

题意

总共有d道题目，最强的LJL每道题目至少都能得一分，最多得f分，所以他每道题目可以随意控制得[1,f]这个区间内的任意一个分数，他想知道有多少可能组成target分。

思路

状态：dp[i][j] 代表 做 i 道题目总分为 j；
方程：dp[i][j] 与 dp[i - 1] 的关系是什么呢？ 第 i道题目LJL得了 k ( 1 <= k <= f)，那么前 i - 1 道题总分为 j - k，对应 dp[i - 1][j - k]；
于是有最终方程：dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j - 2] + … + dp[i - 1][j - f]
边界条件： dp[1][k] = 1 ( 1<= k <= min(target, f) )

代码

#include <bits/stdc++.h>
using namespace std;long long qpow(long long x, long long y) {long long ans = 1;while (y) {if (y & 1)ans = ans * x;y >>= 1;x = x * x;}return ans;
}int solve(int n, int k, int target) {int dp[40][1100];memset(dp, 0, sizeof(int) * 40 * 1100);const int mod = 1e9 + 7;int mm = min(k, target);for (int i = 1; i <= k; i++) {dp[1][i] = 1;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= target; j++) {for (int l = 1; l <= k; l++) {if (j >= l) {dp[i][j] = (dp[i][j] + dp[i - 1][j - l]) % mod;}}}}// dp[i][j] = sum (dp[i-1][j-1],dp[i-1][j-2]...)return dp[n][target];
}int main() {ios::sync_with_stdio(false);int t;cin >> t;while (t--) {int d, f, target;cin >> d >> f >> target;cout << solve(d, f, target) << endl;}return 0;
}

H. 114514

题意

给你一个正整数n,n≤1e7，请你找到最小的n位数x（不允许前导0）满足x同时被11，451，4三个数整除。

解题思路

显而易见，如果x能同时被$11，451，4$三个数整除，则$x$必然是$lcm(11,451,4)$的倍数（$lcm$表示最小公倍数）

$lcm(11,451,4)=1804$

则问题变成给你一个正整数n,n≤1e7，请你找到最小的n位数x%1804=0。

因此我们计算出$10^{n-1}mod1804$（需要手动进行模拟）将其记为$t$，因此结果为$10^{n-1}+(1804-t)$

结果很大，无法直接输出。但是我们发现$t<1804$，所以结果的前$n-4$位必然为$10000000000000......0000$，因此先输出$10000000000000......0000$(共$n-4$位），再输出$t$即可。

细心的同学可能会发现，如果$t=0$即$10^{n-1}$本身就算1804的倍数不是就寄了？答案会多加一个1804。
嗯，很有道理，建议再想想。

上述情况需要特判$n<4,n=4$的情况，不过比较简单，不多赘述

代码

#include<stdio.h>
#include<iostream>
using namespace std;
int main()
{int n;scanf("%d",&n);int now=1;for(int i=1;i<n;i++){now=now*10%1804;	}	if(n<=3){printf("xie'e");}else if(n==4){printf("1804");}else{printf("1");for(int i=1;i<=n-5;i++){printf("0");}printf("%04d",1804-now);}
} 

---

---

I. 大佬的字符串

题意

对字符串s进行任意次如下两种操作，使得最后得到的字符串字典序最小

• 把字符串s开头的一个字符放到字符串a的末尾。
• 把字符串a末尾的一个字符放到字符串b的末尾。

最后s、a都为空

思路

要使得最后得到的字符串字典序最小，显然当字符串a末尾的字符小于等于s串中的最小字符时，就可以把它移到b的末尾。

可以先记录一个后缀最小值，快速判断当前值是否小于等于之后的最小值

代码

#include <bits/stdc++.h>
using namespace std;struct Solution {string getAns(string& str) {vector<char> v(str.size());int size = str.size();v[size - 1] = str[size - 1];int i;for (i = size - 2; i >= 0; i--) {v[i] = min(v[i + 1], str[i]);}string u = "";stack<char> st;// bbadci = 0;while (i < size) {while (st.size() && st.top() <= v[i]) {u += st.top();st.pop();}st.push(str[i]);i++;}while (st.size()) {u += st.top();st.pop();}return u;}
};int main() {ios::sync_with_stdio(false);string s;cin >> s;Solution ss;cout << ss.getAns(s) << endl;return 0;
}

---

---

J. 特殊的合并

解题思路

因为哈夫曼树的带权路径长度最小，所以是哈夫曼裸题，只需要优先队列就可以算出最小值，然后比较和M的大小即可。

代码

#include<bits/stdc++.h>
using namespace std;int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--){int n;cin>>n;priority_queue<int , vector<int > ,greater<int > > Q;for(int i=0;i<n;i++){int a;cin>>a;Q.push(a);}int sum=0;while(Q.size()>1){int a,b;a=Q.top();Q.pop();b=Q.top();Q.pop();sum+=a+b;Q.push(a+b);}int m;cin>>m;if(m>=sum){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}
}

启发题链接：https://codeforces.com/problemset/problem/958/F3

---

---