本文主要是介绍python二次开发Solidworks:方程式驱动曲线,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
如果按照维度去划分,SOLIDWORKS中曲线可以划分为平面曲线和空间曲线,并且在二维草图还是3D草图中都提供了“方程式驱动曲线”。但是从使用方法来讲,方程式驱动的曲线分为两种定义方式:“显性”和“参数式”。“显式方程”在定义了起点和终点处的X值以后,Y值会随着X值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点对应的参数T值范围,X值表达式中含有变量T,同时Y值定义另一个含有T值的表达式,这两个方程式会在T的定义域内求解,从而生成目标曲线。在数学中函数大致也分为显式和隐式,显式函数笔者以常见的正弦函数、一次函数、二次函数为例,参数方和以阿基米德螺线、渐开线、一峰三驻点曲线为例进行示例,其中也包含螺旋线、旋转上升的椭圆线等3D曲线。
下面实现python控制Solidworks绘制渐开线:

import win32com.client as win32
import pythoncom
swApp = win32.Dispatch('sldworks.application')
swApp.Visible = True
Nothing = win32.VARIANT(pythoncom.VT_DISPATCH, None)
Part=swApp.NewDocument(r"C:\ProgramData\SolidWorks\SOLIDWORKS 2018\templates\gb_part.prtdot", 0, 0, 0)
Part.SketchManager.InsertSketch(True)
boolstatus = Part.Extension.SelectByID2("上视基准面", "PLANE", 0, 0, 0, False, 0, Nothing, 0)
Part.ClearSelection2(True)
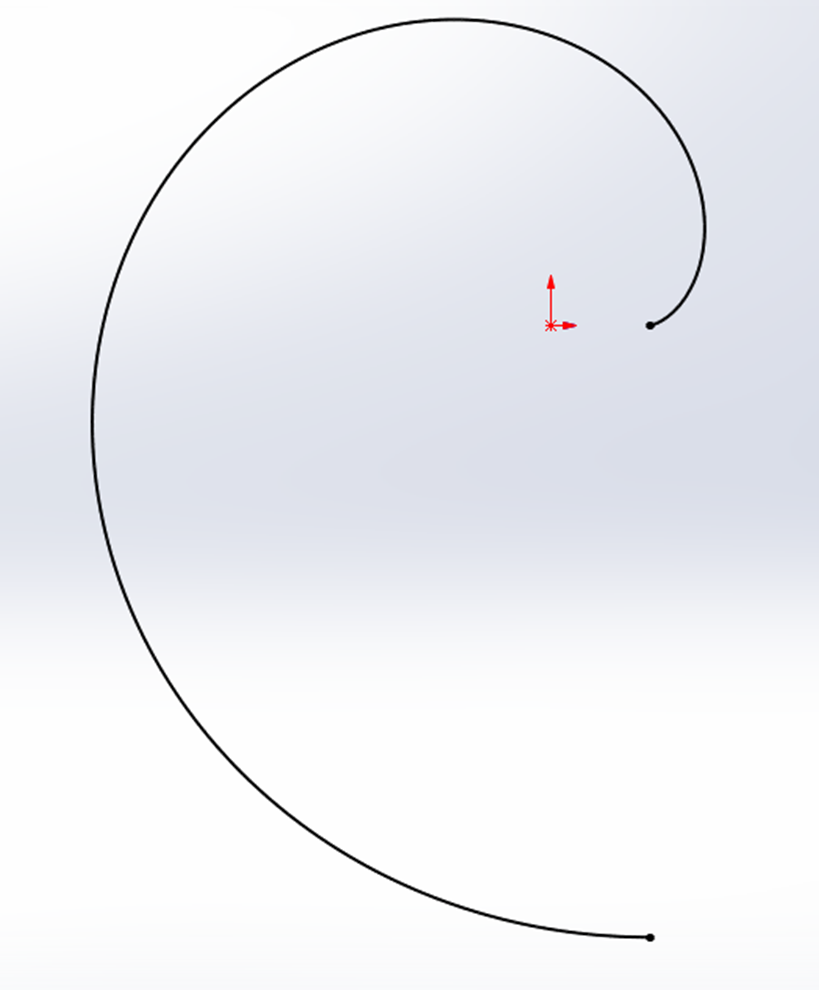
equationDriveCurve = Part.SketchManager.CreateEquationSpline2("5 *(cos(t)+t*sin(t))", "5*( sin(t)-t*cos(t))", "", "0", "2*pi", False, 0, 0, 0, True, True)
Part.ShowNamedView2("*上下二等角轴测", 8)
Part.SelectionManager.EnableContourSelection = False
Part.ViewZoomtofit2()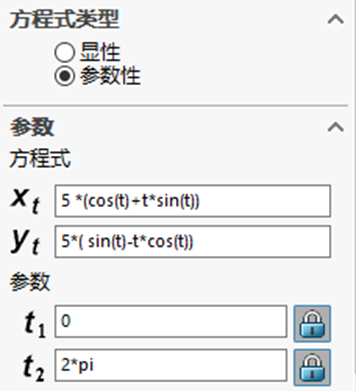
这篇关于python二次开发Solidworks:方程式驱动曲线的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




