matlab桶刻度,结课大作业(求油桶刻度)。。。。。。。

大家好，

先祝大家 中秋节快乐

！

唉，我有20来天没写推文了

。其实吧，前阵子想写一篇关于偏置曲线的算法的推文，但是整了好久，效果不太好，不通用(只对连续且平缓的曲线效果好)，所以最后就没写成推文了。

这周二呢，MATLAB课上老师把结课的大作业题给布置好了，我当天晚上回来就抽了时间给做了

，但是呢最后累积下来的误差太大了。。。。。。

昨天又换了一个方法给重写了一遍，这回就差不多了

把题说一下吧：

如图所示。

先说一下我最开始做的那个误差比较大的方法的思路：

1.柱体的体积是底面积乘以高，这个高是固定的8m。

2. 每刻度之间是5m³，那么每刻度之间的面积是5/8。

3.以椭圆中心为坐标原点建立一个坐标系，那么就可以取椭圆的一半(y轴的右半部分)来算了，下面都是以半个椭圆来说的。

4.那么每刻度之间的面积是5/16；

5. 我最先想到的就是定积分的定义：微分，求和。每个刻度之间可以微分成好多好多个小条(沿y轴方向微分)，那个每个小条的面积就是dy(i)*x(i)。当我这些小条的面积累加到5/16时便是一个刻度了，然后记录下来，直到刻度超过2就停止累加的这个循环。

大概思路就是这样，代码就不给了，下面给出这种方法得出的结果：

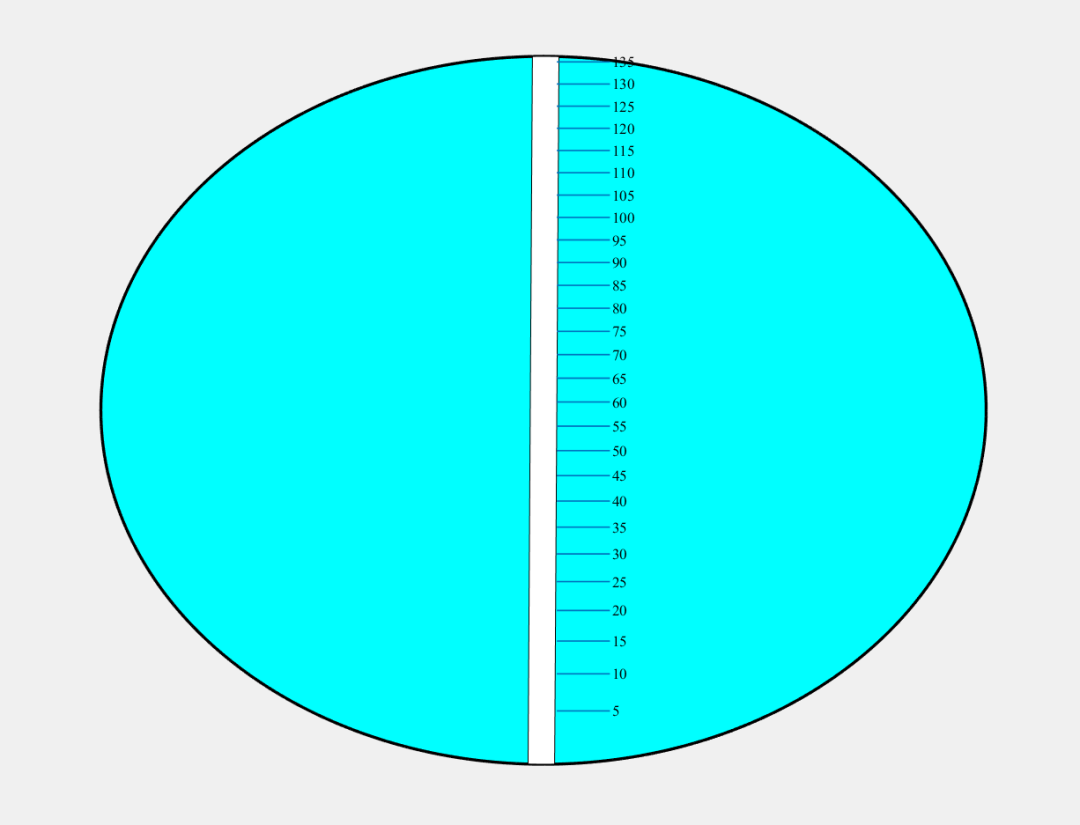
本该到125就结束的，最后体积多了10多

后来改正后的思路：

上面的前4条还是没变，只是不再直接地用简单的微分求和来计算面积

，椭圆的右半边是可以写成

x = f(y)

这样一个y是自变量，x是因变量的显式函数的，所以我们最后可以写出一个变上限函数，进而就转化成了一个求零点的问题

，这样就会比上面那个精确不少了，这里没有误差的累积。

下面还是一步一步来说吧：

1.椭圆的方程：

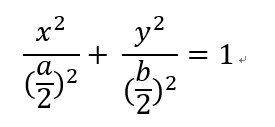
其中：a是长轴长，b是短轴长。

2.求出 x：

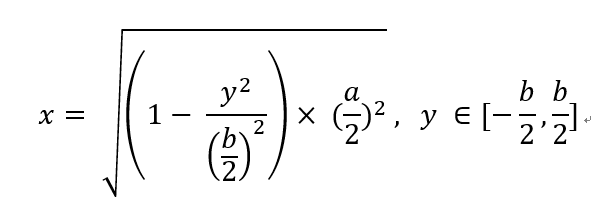
这个算的是右半边的。

3.设：y0，y1 ∈ [-b/2, b/2]，s.t.：

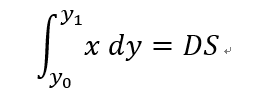
其中：DS是在右半个椭圆中两个刻度所夹的面积，

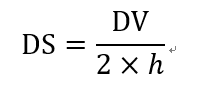
y0初值为 -b/2，y1才是变量。

4.令：

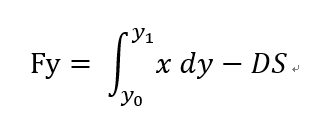
5.要做的就是在 [-b/2, b/2]这个区间上寻找Fy的零点: y1，然后把这个y1赋值给y0，再去寻找新的y1，这样的循环共执行 fix(V/DV) 次

要按照我后面的这个思路做的话，需要知道MATLAB中计算数值积分的几个函数：quad, quadgk, integral, .........这几个都还行，

quad：适用于精度要求低，被积函数平滑性较差的数值积分[1]

quadgk：适用于高精度和震荡数值积分，支持无穷区间，并且能够处理端点包含奇点的情况，同时还支持沿着不连续函数积分，复数域线性路径的围道积分法[1]

具体用法这里不介绍，

源代码

一共有3个m文件：

第一个是主程序，如下：

clc

clear

close all

tic

%%

%%% 定义输入参数：

%%%

data.a = 5; % 长轴长

data.b = 4; % 短轴长

data.h = 8; % 油桶高

data.DV = 5; % 每刻度之间的体积

%%

%%% 计算刻度

h_ticks = SolTick_v2(data);

%%% 绘制刻度

drawTick(data, h_ticks)

toc

第二个是计算刻度的函数：

function h_ticks = SolTick_v2(data)

a = data.a; % 长轴长

b = data.b; % 短轴长

h = data.h; % 油桶高

DV = data.DV; % 每刻度之间的体积

DS = DV / h; % 每刻度之间的面积

n = fix(pi * (a/2) * (b/2) / DS);  % 刻度的个数

%%

%%% 计算时以一半来计算，保证了从最底端开始每层体积是DV，最上面肯定会多出一点点

DS = DS / 2; % 每刻度之间的面积(取了一半)

h_tick0 = -b/2; % 刻度由下往上的起始位置设置为h_tick的初始值

h_ticks = zeros(1, n); % 先假定有20个刻度，后面多了就删，少了就补(自动扩充)

for k =  1:n

x=@(y)sqrt((1 - y.^2 ./ (b/2)^2) * (a/2)^2);

Fy=@(h_tick)quadgk(x,h_tick0, h_tick) - DS;

[h_tick0, ~, ~] = fzero(Fy, [-b/2, b/2]);

h_ticks(k) = h_tick0; % 保存此时的刻度

end

这个文件中黄色加粗的那三句话是整个的核心。前两句对应上面的第2步和第4步，定义了两个函数。第三句对应上面的第5步，求解零点。

第三个是绘制刻度的函数：

function drawTick(data, h_ticks)

a = data.a; % 长轴长

b = data.b; % 短轴长

t = 0 : 0.001 : 2*pi;

x = a/2 .* cos(t);

y = b/2 .* sin(t);

ax = axes('Visible', 'off');

ax.NextPlot = 'add';

H_oval = patch(x, y, 'c');

H_oval.Parent = ax;

H_oval.LineWidth = 2;

H_oval.EdgeColor = [0 0 0];

drawBarTick(ax, data, h_ticks)

daspect([1 1 1])

end

function drawBarTick(parent, data, h_ticks)

a = data.a; % 长轴长

b = data.b; % 短轴长

t1 = pi/2 - pi/90 :0.01: pi/2 + pi/90;

t2 = -pi/2 - pi/90 :0.01: -pi/2 + pi/90;

x1 = a/2 .* cos(t1);

y1 = b/2 .* sin(t1);

x2 = a/2 .* cos(t2);

y2 = b/2 .* sin(t2);

x = [x1, x2];

y = [y1, y2];

H_bar = patch(x, y, 'w');

H_bar.Parent = parent;

%%

%%% tick 是由下向上的。

for i = 1:length(h_ticks)

tick = h_ticks(i);

x_tick = (x1(1) + x2(end)) / 2;

H_tick = line([x_tick x_tick+0.3], [tick tick]);

H_tick.LineWidth = 1;

H_text = text(x1(1)+0.3, tick, num2str(5*i));

H_text.FontName = 'Times New Roman';

H_text.FontSize = 10;

end

end

最后的计算结果：

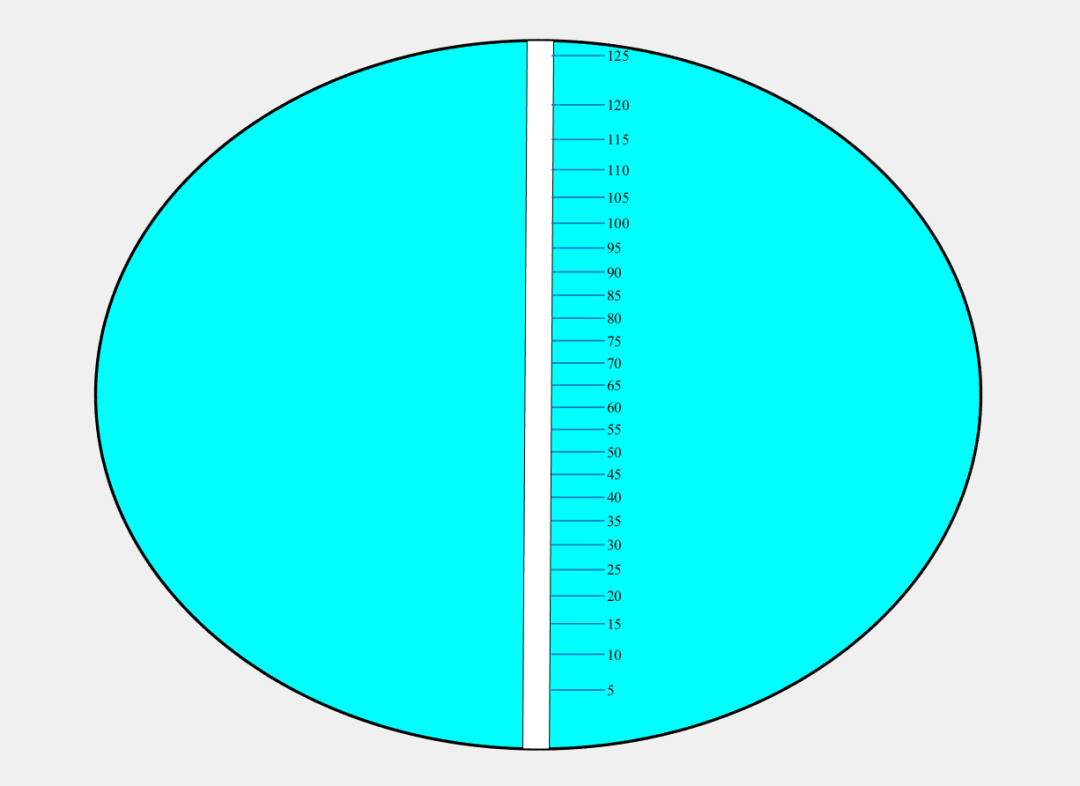
为了便于计算不同油桶参数下的刻度，我还另外制作了一个界面

，如下：

点击GENERATE按钮便可以生成图形，以及刻度，如下：

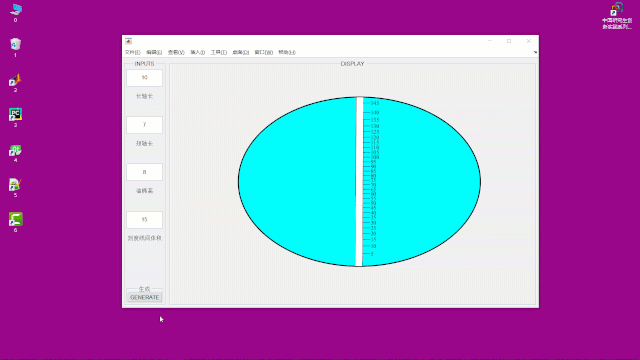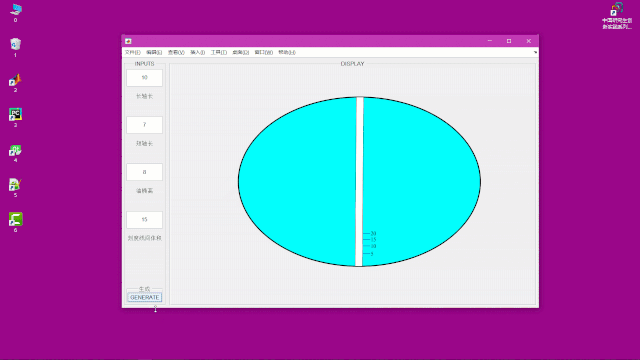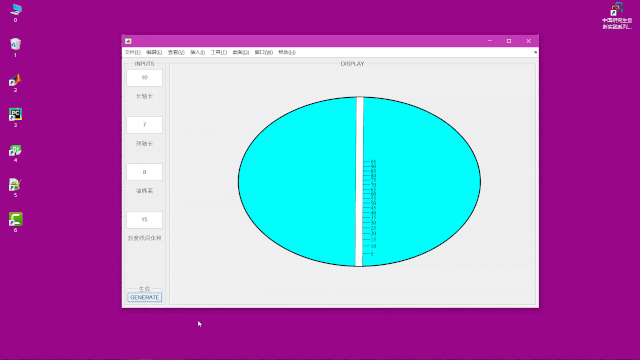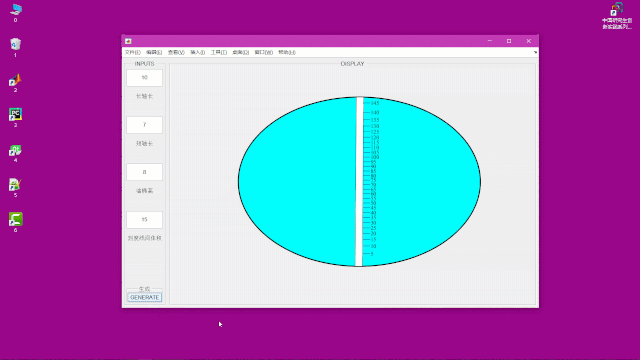
关于GUI的制作的代码这次就不分享了

[1] https://blog.csdn.net/superldxu/article/details/53080370

--END--